Sea $f : A \subseteq \mathbb{R}^2 \rightarrow B \subseteq \mathbb{R}^2$ diferenciable.

Consideremos para todo punto $\vec{a} \in A$ y para cualesquiera dos vectores $\vec{v_1}$, $\vec{v_2}$ tangentes a curvas que pasen por $\vec{a}$

$\vec{v_1} = {{\alpha}_1 \, }’ (0) \; \; \; \; \; \; \; \; \; \; \vec{v_2 } = {{\alpha}_2 \, }’ (0)$

$ {\alpha}_1 (0) = \vec{a} \; \; \; \; \; \; \; \; \; \; {\alpha}_2 (0) = \vec{a}$

Consideremos el ángulo que forman $\vec{v_1}$ y $\vec{v_2}$.

Consideremos las curvas:

$\beta_1 (t) = f \, ( \alpha_1 \, (t))$

$\beta_2 (t) = f \, ( \alpha_2 \, (t))$

dos curvas distintas que pasan por $f (\vec{a})$.

Y además,

$\vec{w_1} = {\beta_1}’ (0) $

$\vec{w_2} = {\beta_2}’ (0) $

Y consideremos el ángulo que forman $\vec{w_1}$ y $\vec{w_2} $.

Decimos que $f$ es conforme si los dos ángulos son iguales y preservan la orientación de la base. Si invierten la orientación, diremos que $f$ es anticonforme.

$\vec{w_1} = df_{\vec{a}} (\vec{v_1}) $

$\vec{w_2} = df_{\vec{a}} (\vec{v_2}) $

Luego

$\cos \theta = \dfrac{ \langle \vec{v_1} , \vec{v_2} \rangle}{\big\| \vec{v_1} \big\| \big\| \vec{v_2} \big\|} = \dfrac{ \langle \vec{w_1} , \vec{w_2} \rangle}{\big\| \vec{w_1} \big\| \big\| \vec{w_2} \big\|} = \cos \varphi$

En esta entrada vamos a hacer lo siguiente:

1. Deducir la regla de correspondencia analítica de la inversión con respecto a la circunferencia unitaria, a partir de la definición usada en los cursos de geometría moderna.
2. Deducir algunas de sus propiedades geométricas, en particular como son las imágenes de las rectas y las circunferencias bajo la inversión.
3. Finalmente veremos que la inversión es anticonforme, es decir, que preserva las magnitudes de los ángulos entre curvas, pero invierte el sentido de los mismos.

1. Regla de correspondencia de la inversión:

$ f : \mathbb{R}^2 \setminus \{(0, 0) \} \rightarrow \mathbb{R}^2 \setminus \{(0, 0) \}$

$\mathcal{C} : x^2 + y^2 = 1$

$P \rightarrow {P \, }’$ tal que:

(1) ${P \, }’$ está en el rayo $\overrightarrow{OP}$.

(2) $O{P \, }’ \cdot OP = r^2 = 1$

Sea $ P = (x, y)$, ${P \, }’ = (u, v)$.

${P \, }’ $ en el rayo $\overrightarrow{OP}$ significa que $(u, v) = \lambda (x, y)$, con $\lambda > 0$.

Para saber la regla de correspondencia basta con determinar $\lambda$.

Además, de (2) se tiene que:

$\sqrt{u^2 + v^2} \sqrt{x^2 + y^2} = 1$

$(u^2 + v^2) (x^2 + y^2) = 1$

$({\lambda}^2x^2 + {\lambda}^2y^2) (x^2 + y^2) = 1$

${\lambda}^2(x^2 + y^2)^2 = 1$

${\lambda} (x^2 + y^2) = 1$

${\lambda} = \dfrac{1}{(x^2 + y^2)}$

Luego $u = \dfrac{x}{x^2 + y^2}$ y $v = \dfrac{y}{x^2 + y^2}$

2. Propiedades geométricas

(*) $f$ lleva rayos que emanan del origen en rayos que emanan del origen pero, los recorre en sentido contrario.

$\alpha (t) = \big( t \cos {\theta}_0, t \sin {\theta}_0 \big)$ es la recta parametrizada con $t \in (0, \infty)$

Si $x = t \cos {\theta}_0 \; \Rightarrow \; x^2 = t^2 \cos^2 {\theta}_0$

$y = t \sin {\theta}_0 \; \Rightarrow \; y^2 = t^2 \sin^2 {\theta}_0$

entonces $x^2 + y^2 = t^2$

Luego $u = \dfrac{x}{x^2 + y^2} = \dfrac{t \cos {\theta}_0}{t^2}$ entonces $ u = \dfrac{1}{t} \cos {\theta}_0 $

Análogamente, $ v = \dfrac{1}{t} \sin {\theta}_0 $

En el siguiente enlace puedes observar la animación de como se desplaza un punto sobre una circunferencia y el sentido en el que se desplaza el punto que resulta de la inversión.

https://www.geogebra.org/classic/wtmhq2d2

(*) $f$ lleva circunferencias de radio $r_0$ con centro en el origen en circunferencias de radio $\frac{1}{r_0}$ con centro en el origen. Se deja como ejercicio al lector comprobar esta propiedad.

3. $f$ es anticonforme

Vamos a ver que $f$ es anticonforme en el punto $a = (2, 0)$

Consideremos dos curvas que pasan por $a$

$\alpha (t) = (2, 0) + t (1, 0)$ con $t \in ( \, – \, 2 , \infty)$, y

$\beta (t) = (2 \cos t , 2 \sin t)$ con $t \in \mathbb{R}$

Las dos curvas efectivamente pasan por $a$ cuando $t=0$. Pues $\alpha (0) = a $ y $\beta (0) = a $. Sin embargo, $\alpha’ (0)= (1,0)$ y $\beta’ (0)=(0,2)$. Estos dos vectores son ortogonales, y se va del primero al segundo en el sentido contrario al de las manecillas del reloj. Ahora vamos a calcular la diferencial de $f$ en el punto $a$.

$u = \dfrac{x}{x^2 + y^2}$, $v = \dfrac{y}{x^2 + y^2}$

$df = \begin{pmatrix} \dfrac{\partial u}{\partial x} & \dfrac{\partial u}{\partial y} \\ \\ \dfrac{\partial v}{\partial x} & \dfrac{\partial v}{\partial y} \end{pmatrix} = \begin{pmatrix} \dfrac{y^2 \, – \, x^2}{(x^2 + y^2)^2} & \dfrac{\, – \, 2xy}{(x^2 + y^2)^2} \\ \\ \dfrac{\, – \, 2xy}{(x^2 + y^2)^2} & \dfrac{x^2 \, – \, y^2}{(x^2 + y^2)^2} \end{pmatrix}$

En el punto $a = (2, 0)$ la matriz $df$ es:

$\begin{pmatrix} – \, \dfrac{4}{16} & 0 \\ \\ 0 & \dfrac{4}{16} \end{pmatrix} = \begin{pmatrix} – \, \dfrac{1}{4} & 0 \\ \\ 0 & \dfrac{1}{4} \end{pmatrix} $

Entonces $df_{\vec{a}} ({\alpha \, }’ (0) ) = \begin{pmatrix} – \, \dfrac{1}{4} & 0 \\ \\ 0 & \dfrac{1}{4} \end{pmatrix} \begin{pmatrix} 1 \\ \\ 0 \end{pmatrix} = \begin{pmatrix} – \, \dfrac{1}{4} \\ \\ 0 \end{pmatrix}$

Este vector está anclado en $f(\alpha(0))=f(2,0)=(\dfrac{1}{2},0)$.

Análogamente,

$df_{a} ({\beta \, }’ (0) ) = \begin{pmatrix} – \, \dfrac{1}{4} & 0 \\ \\ 0 & \dfrac{1}{4} \end{pmatrix} \begin{pmatrix} 0 \\ \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ \\ \dfrac{1}{2} \end{pmatrix}$

Este vector está anclado en $f(\beta(0))=f(2,0)=(\dfrac{1}{2},0)$.

Observamos que $df_{a}(\alpha'(0))$ y $df_{a}(\beta'(0))$ resultaron ser vectores ortogonales. Además, para ir del primero al segundo hay que ir en el sentido de las manecillas del reloj. Aquí estamos viendo que se preserva la magnitud del ángulo pero se invierte el sentido.

Observamos que la matriz $df_{a}$ es diagonal y en la diagonal tiene el mismo número salvo signo. Esta matriz es el producto de una matriz diagonal con el número $\frac{1}{4}$ en la diagonal, por una matriz que en la diagonal tiene $1$ y $-1$. Entonces es el producto de una homotecia con factor $\frac{1}{4}$ seguida de una reflexión. La homotecia preserva los ángulos y la reflexión invierte su sentido.

En el siguiente enlace puedes observar la animación correspondiente a este análisis.

https://www.geogebra.org/classic/b97afcj6

Tres alelos ( formas naturales de genes) $A$, $B$ y $O$ determinan los tres tipos sanguíneos.

$$ \begin{align*} A &\iff (AA \, \, \circ \, \, AO ) \\ B &\iff (BB \, \, \circ \, \, BO) \\ O &\iff ( OO) \\ AB &\iff ( AB ) \end{align*}$$

La ley de Hardy – Weinberg establece que la proporción $P$ de individuos de una población que llevan los alelos diferentes está dada por la expresión:

$$P = 2pq \, + \, 2pr \, + \, 2qr$$

donde $p$, $q$ y $r$ son las proporciones de alelos $A$, $B$ y $O$ en dicha población.

Use el hecho de que $ p + q + r = 1$ para demostrar que $p \leq \dfrac{2}{3}$

(Nótese que la proporción de individuos en la población que lleva dos alelos iguales es $ p^2+q^2+r^2$)

Maximizar $P = 2pq \, + \, 2pr \, + \, 2qr$ sujeta a $ p + q + r = 1$,

restricción $ Q (p, q, r) = p + q + r \, – \, 1 = 0$, con $p, q, r, \geq 0$

Usando multiplicadores de Lagrange $\nabla P = \Bigg( \dfrac{\partial P}{\partial p}, \dfrac{\partial P}{\partial q}, \dfrac{\partial P}{\partial r} \Bigg)$ entonces,

$\nabla P = \big( 2q + 2r , 2p + 2r , 2p + 2q \big)$

$\nabla Q = ( 1 , 1, 1 )$

Vamos a examinar en qué puntos del triángulo la función $P(p,q,r)$ alcanza sus valores extremos.

a) ¿Qué pasa en el interior del simplejo (triángulo)?

b) ¿Qué pasa en las aristas?

c) ¿Qué pasa en los vértices?

a) Si un valor extremo se alcanza en el interior del triángulo, entonces lo podemos encontrar con el método de multiplicadores de Lagrange con una restricción. $$\nabla P = \lambda \nabla Q$$

$\begin{pmatrix} 2q + 2r \\ \\ 2p + 2r \\ \\ 2p + 2q \end{pmatrix} = \lambda \begin{pmatrix} 1 \\ \\ 1 \\ \\ 1 \end{pmatrix}$

$\begin{align*} 2q + 2r &= \lambda\\ \\ 2p + 2r &= \lambda \\ \\ 2p + 2q &= \lambda \end{align*}$

Sumando

$4p + 4q + 4r = 3 \lambda$

$4 ( p + q + r) = 3 \lambda$, como $ p + q + r = 1$, entonces

$4 = 3 \lambda$ por lo que $\lambda = \dfrac{4}{3}$

Luego, sustituyendo en el sistema anterior se tiene que:

$$p = \dfrac{1}{3}\, , \, q = \dfrac{1}{3} \, , \, r = \dfrac{1}{3}$$

Entonces

$P \Bigg( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Bigg) = 2 \Bigg( \dfrac{1}{9} \Bigg) + 2 \Bigg( \dfrac{1}{9} \Bigg) + 2 \Bigg( \dfrac{1}{9} \Bigg) = \dfrac{6}{9} = \dfrac{2}{3}$

c) En los vértices evaluamos el valor de la función, porque ahí también puede haber un valor extremo:

$P ( 1, 0, 0) = 0$

$P ( 0, 1, 0) = 0$

$P ( 0, 0, 1) = 0$

b) En este caso, en cada arista una variable es constante, y podemos reducir el problema a encontrar los valores extremos de una función de dos variables sujeta a una restricción, de nuevo, usaremos multiplicadores de Lagrange.

Hay tres aristas, cuando $p = 0$, $q = 0$ o $r = 0$

Analicemos que sucede si $r = 0$, entonces $P (p, q, 0) = 2pq$

Ahora el problema es maximizar $2pq$, sujeta a $ p + q = 1$ con $p, q \geq 0$, entonces

$ p = q = \frac{1}{2}$ y $P (\frac{1}{2}, \frac{1}{2}, 0) = \frac{1}{2}$

Análogamente para las otras aristas se obtienen los puntos $ (0, \frac{1}{2}, \frac{1}{2})$ y $ (\frac{1}{2}, 0, \frac{1}{2})$, donde $P$ para cada uno de ellos es $\frac{1}{2}$.

En la siguiente tabla puedes observar el valor de la función en cada uno de los puntos especiales analizados: vértices, puntos medios de los lados y el punto calculado en el inciso (a) $\Big( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Big)$.

Por lo tanto, de lo analizado anteriormente vemos que el valor máximo de $P$ es $\frac{2}{3}$ y se obtiene en el punto $ \Bigg( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Bigg)$.

Sea $ f : \mathbb{R}^3 \rightarrow \mathbb{R}$ sujeta a dos restricciones:

$g_1 (x, y, z) = 0$

$g_2 (x, y, z) = 0$

Hipótesis:

Para todo $ \vec{p} \in {g_1}^{-1} (0) \cap {g_2}^{-1} (0) \neq \emptyset$ los gradientes $\nabla g_1 (\vec{p})$ y $\nabla g_2 (\vec{p})$ son linealmente independientes.

Sea $\vec{q}$ un punto en donde $f\big|_{{g_1}^{-1} (0) \cap {g_2}^{-1} (0)}$ alcanza un valor extremo, le aplicamos el teorema de la función implícita a $G : \mathbb{R}^3 \rightarrow \mathbb{R}^2$ tal que $(x, y, z) \rightarrow \big( g_1 (x, y, z), g_2 (x, y, z) \big)$

Sin pérdida de generalidad, supongamos $\begin{align*} x = h_1 (z) \\ y = h_2 (z) \end{align*}$

$f\big|_{{g_1}^{-1} (0) \cap {g_2}^{-1} (0)}$ puede verse como una función $\mathcal{I} \subseteq \mathbb{R} \rightarrow \mathcal{J} \subseteq \mathbb{R}$ tal que

$z \rightarrow f \big( h_1 (x, y, z) , h_2 (x, y, z) , z \big)$

Entonces $ (x, y, z)$ es solución del sistema de ecuaciones cerca del punto $\vec{q}$ si y sólo si

$x = h_1 (z)$

$y = h_2 (z)$

$\alpha (z) = \big( h_1 (x, y, z) , h_2 (x, y, z) , z \big)$ parametriza un «pedacito» de curva (que pasa por $\vec{q}$).

Maximizar $f ( \alpha (z) )$

Derivando

$\nabla f \big( \alpha (z) \big) \cdot {\alpha \, }’ (z) = \Big( \dfrac{\partial f}{\partial x} , \dfrac{\partial f}{\partial y} , \dfrac{\partial f}{\partial z} \Big) \cdot \Big( {h_1}’ , {h_2}’ , 1 \Big) = 0$

$\dfrac{\partial f}{\partial x} {h_1}’ \, + \, \dfrac{\partial f}{\partial y} {h_2}’ \, + \, \dfrac{\partial f}{\partial z} = 0$

Luego $\nabla f$ es ortogonal a ${\alpha \, }’$, es decir, $\nabla f$ está en el plano generado por $\nabla g_1$ y $\nabla g_2$, es decir,

$$\nabla f = \lambda_1 \nabla g_1 \, + \, \lambda_2 \nabla g_2$$

El teorema de la función implícita se usa para determinar si el conjunto de soluciones de un sistema de ecuaciones es una curva suave o una superficie suave o una variedad suave.

Una ecuación con dos variables

$f (x, y) = 0$

$f^{-1} (0) = \big\{ (x, y) \in \mathbb{R}^2 \big| f (x, y) = 0 \big\}$ conjunto de nivel.

Supongamos que conocemos un punto en $f^{-1}(0)$. Las posibilidades para este conjunto de nivel son:

*) Podría ser un punto,

**) podría ser una o varias curvas que se cruzan, o

***) podría ser una curva con picos.

Para que sea una curva sin picos se debe cumplir las siguientes condiciones:

$f : \mathbb{R}^2 \rightarrow \mathbb{R} $ de clase $\mathcal{C}^1$, $f^{-1} (0) \neq \emptyset$

$\nabla f (p) \neq \vec{0}$, para todo $p \in f^{-1} (0)$

Entonces, $f^{-1} (0)$ es una curva suave sin autointersecciones.

Si $\nabla f (p) \neq \vec{0}$, entonces

a) $\dfrac{\partial f}{\partial x} (p) \neq 0$ entonces existe una función $g$ tal que, cerca de $p$, $f^{-1} (0)$ es la gráfica de $x = g (y)$; o

b) $\dfrac{\partial f}{\partial y} (p) \neq 0$ entonces existe una función $h$ tal que, cerca de $p$, $f^{-1} (0)$ es la gráfica de $y = h (x)$

Una ecuación con tres variables

$f (x, y, z) = 0$

$f^{-1} (0) = \big\{ (x, y, z) \in \mathbb{R}^3 \big| f (x, y) = 0 \big\}$ conjunto de nivel.

Supongamos que conocemos un punto en $f^{-1}(0)$. Las posibilidades para este conjunto de nivel son:

*) Podría ser un punto,

**) podría ser una o varias superficies que se cruzan, o

***) podría ser una superficie con «pellizcos».

Condiciones

$f^{-1} (0) \neq \emptyset$, con $f : \mathbb{R}^3 \rightarrow \mathbb{R}$ de clase $\mathbb{C}^1$

$\nabla f (\vec{p}) \neq \vec{0}$ para todo $\vec{p} \in f^{-1} (0) $

Entonces $f^{-1} (0) $ es una superficie suave sin autointersecciones.

Si $\nabla f (\vec{p}) \neq \vec{0}$ entonces:

i) $\dfrac{\partial f}{\partial x} (\vec{p}) \neq 0$ entonces existe $g $ tal que $ x = g (y, z)$

ii) $\dfrac{\partial f}{\partial y} (\vec{p}) \neq 0$ entonces existe $h $ tal que $ y = h (x, z)$

iii) $\dfrac{\partial f}{\partial z} (\vec{p}) \neq 0$ entonces existe $\varphi $ tal que $ z = \varphi (x , y)$

Dos ecuaciones con tres variables

$f (x, y, z) = 0$

$g (x, y, z) = 0$

Supongamos que el conjunto de soluciones es no vacío.

¿Qué podría ser?

*) Podría ser un punto.

**) Podría ser una o varias curvas que se cruzan.

***) Podría ser una curva con picos.

Condición

Sea $F : \mathbb{R}^3 \rightarrow \mathbb{R}^2$ tal que

$F (x, y, z) = \big( f (x, y, z), g (x, y, z) \big)$

El conjunto de soluciones del sistema de ecuaciones

$f (x, y, z) = 0$

$g (x, y, z) = 0$

podemos verlo de dos formas

a) como la intersección de dos conjuntos de nivel

$$ f^{-1} (0) \cap g^{-1} (0)$$

b) como la imagen inversa de $(0,0)$ bajo $ F $, es decir $ F^{-1} (0, 0).$

${}$

Si pedimos que $\nabla f (\vec{p}) \neq \vec{0} $ y que $\nabla g (\vec{p}) \neq \vec{0} $ para todo $\vec{p} \in f^{-1} (0) \cap g^{-1} (0)$, lo único que podemos concluir es que localmente, el conjunto de soluciones es la intersección de dos superficies suaves

$ \nabla f = ( 0, 0, 1) \; \; \; \; \; \; \; \; \; \; f (x, y, z) = z$

$ \nabla g = ( 2x, \, – \, 2y, \, – \, 1 ) \; \; \; \; \; \; \; \; \; \; g (x, y, z) = x^2 \, – \, y^2 \, – \, z$

$f^{-1} (0) $ plano $z = 0$

$ g^{-1} (0)$ es la silla $ z = x^2 \, – \, y^2$

En el siguiente enlace, puedes observar las gráficas de $f^{-1} (0) $ y $g^{-1} (0) $, así como su intersección.

https://www.geogebra.org/classic/y8cum2au

En este caso la intersección consiste de dos rectas que se cruzan. Para evitar situaciones como esta necesitamos que

$\nabla f (\vec{p})$ y $\nabla g (\vec{p})$ sean linealmente independientes en todo $ \vec{p} \in f^{-1} (0) \cap g^{-1} (0)$.

La matriz de la diferencial de $F$ en $\vec{p}$ es

$$\begin{pmatrix} \dfrac{\partial f}{\partial x} (\vec{p}) & \dfrac{\partial f}{\partial y} (\vec{p}) & \dfrac{\partial f}{\partial z} (\vec{p}) \\ \\ \dfrac{\partial g}{\partial x} (\vec{p}) & \dfrac{\partial g}{\partial y} (\vec{p}) & \dfrac{\partial g}{\partial z} (\vec{p}) \end{pmatrix}$$

¿Qué condiciones debemos pedir en este caso?

Que los gradientes de $f $ y $g$ sean linealmente independientes.

Equivalentemente, que la matriz tenga rango 2.

Equivalentemente, que al menos un subdeterminante de 2×2 (un menor) sea distinto de CERO. De esta última condición, tenemos tres posibilidades:

a) $\begin{vmatrix} \dfrac{\partial f}{\partial x} (\vec{p}) & \dfrac{\partial f}{\partial y} (\vec{p}) \\ \\ \dfrac{\partial g}{\partial x} (\vec{p}) & \dfrac{\partial g}{\partial y} (\vec{p}) \end{vmatrix}\neq 0$

b) $\begin{vmatrix} \dfrac{\partial f}{\partial x} (\vec{p}) & \dfrac{\partial f}{\partial z} (\vec{p}) \\ \\ \dfrac{\partial g}{\partial x} (\vec{p}) & \dfrac{\partial g}{\partial z} (\vec{p}) \end{vmatrix}\neq 0$

c) $\begin{vmatrix} \dfrac{\partial f}{\partial y} (\vec{p}) & \dfrac{\partial f}{\partial z} (\vec{p}) \\ \\ \dfrac{\partial g}{\partial y} (\vec{p}) & \dfrac{\partial g}{\partial z} (\vec{p}) \end{vmatrix}\neq 0$

Si a) se cumple, entonces

$x = h_1 (z)$

$y = h_2 (z)$

Si b) se cumple, entonces

$x = g_1 (y)$

$z = g_2 (y)$

Si c) se cumple, entonces

$y = \varphi_1 (x)$

$z = \varphi_2 (x)$

Veamos un ejemplo de este tipo.

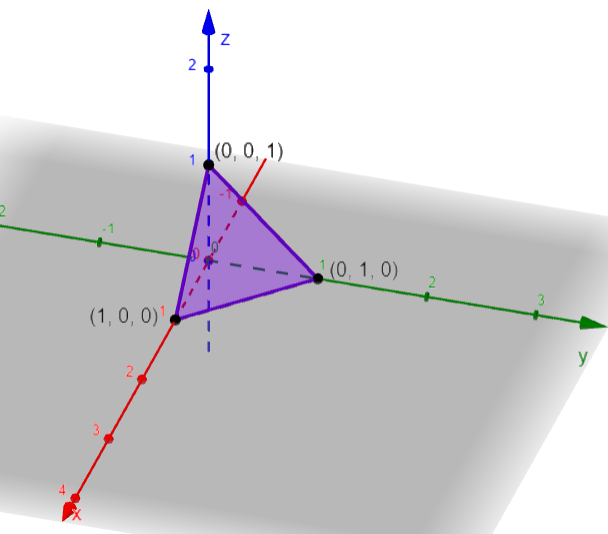
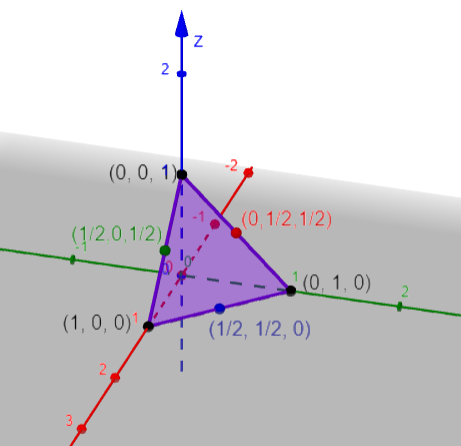
Sea $F (x, y, z) = \big( x^2 + y^2 + z^2 \, – \, 1 , x + y + z \, – \, 1\big)$

$ f (x, y, z) = x^2 + y^2 + z^2 \, – \, 1 = 0$, esfera de radio 1 y centro $(0, 0, 0)$, y

$ g (x, y, z) = x + y + z \, – \, 1 = 0$, plano que pasa por: $(1, 0, 0)$, $(0, 1, 0)$ y $(0, 0, 1)$.

En la siguiente animación puedes observar las gráficas de $f$ y $g$.

https://www.geogebra.org/classic/yvduga9b

La matriz de la diferencial de $F$ en $\vec{p}$ es

$\begin{pmatrix} 2x & 2y & 2z \\ \\ 1 & 1 & 1 \end{pmatrix}$

Tomemos el punto $( 0, 0 , 1)$, luego analizamos los menores en ese punto:

$\begin{vmatrix} 0 & 0 \\ \\ 1 & 1 \end{vmatrix} = 0$

$\begin{vmatrix} 0 & 2 \\ \\ 1 & 1 \end{vmatrix} = – \, 2 \neq 0 $ entonces $x = g_1 (y) ; z = g_2 (y)$

$\begin{vmatrix} 0 & 2 \\ \\ 1 & 1 \end{vmatrix} = – \, 2 \neq 0 $ entonces $y = \varphi_1 (x) ; z = \varphi_2 (x)$

Luego, puedo elegir cualquiera de estas últimas dos opciones.

En ninguna vecindad del $(0, 0, 1)$ en la circunferencia se parametriza como función de $z$

$$\alpha (z) = \big( x (z), y (z), z \big)$$

$\alpha : (\, – \, \epsilon , \epsilon) \subset \mathbb{R} \rightarrow \mathbb{R}^3$

$\alpha (x) = \big( x , \varphi (x), \psi (x) \big)$ entonces $ y = \varphi (x)$ y $ z = \psi (x)$ parametriza una vecindad del conjunto de soluciones cerca del punto $(0, 0, 1)$.

$ \begin{equation*} \left\{ \begin{aligned} x^2 + \varphi (x)^2 + \psi (x)^2 &= 1 \\ \\ x + \varphi (x) + \psi (x) &= 1 \end{aligned} \right. \end{equation*}$

Derivando con respecto a $x$

$ \begin{equation*} \left\{ \begin{aligned} \cancel{2}x + \cancel{2}\varphi (x) + \cancel{2} \psi (x) &= 0 \\ \\ 1 + {\varphi \, }’ (x) + {\psi \, }’ (x) &= 0 \end{aligned} \right. \end{equation*}$

$\begin{pmatrix} \varphi (x) & \psi (x) \\ \\ 1 & 1 \end{pmatrix} \begin{pmatrix} {\varphi \, }’ (x) \\ \\ {\psi \, }’ (x) \end{pmatrix} = \begin{pmatrix} \, – \, x \\ \\ \, – \, 1 \end{pmatrix}$

entonces en el punto $p = ( 0, 0, 1) = \alpha (0)$

$\varphi (0) = 0$

$\psi (0) = 1$

se tiene que

$\begin{pmatrix} 0 & 1 \\ \\ 1 & 1 \end{pmatrix} \begin{pmatrix} {\varphi \, }’ (0) \\ \\ {\psi \, }’ (0) \end{pmatrix} = \begin{pmatrix} 0 \\ \\ \, – \, 1 \end{pmatrix}$

Entonces

$ \begin{pmatrix} {\varphi \, }’ (0) \\ \\ {\psi \, }’ (0) \end{pmatrix} = {\begin{pmatrix} 0 & 1 \\ \\ 1 & 1 \end{pmatrix}}^{-1} \begin{pmatrix} 0 \\ \\ \, – \, 1 \end{pmatrix}$

$ \begin{pmatrix} {\varphi \, }’ (0) \\ \\ {\psi \, }’ (0) \end{pmatrix} = {\begin{pmatrix} \, – \, 1 & 1 \\ \\ 1 & 0 \end{pmatrix}} \begin{pmatrix} 0 \\ \\ \, – \, 1 \end{pmatrix} = \begin{pmatrix} \, – \, 1 \\ \\ 0 \end{pmatrix}$

Entonces ${\alpha \, }’ (0) = (1, \, – \, 1, 0 )$

Idea general, bajo condiciones adecuadas «genéricas» las propiedades de la derivada (de la diferencial; de la mejor aproximación lineal cerca del punto) se heredan a la función.

Si $ F : \mathbb{R}^2 \rightarrow \mathbb{R}^2$, $F (f, g)$

$d F_p : \mathbb{R}^2 \rightarrow \mathbb{R}^2$

$\begin{pmatrix} f_x (\vec{p}) & f_y (\vec{p}) \\ \\ g_x (\vec{p}) & g_y (\vec{p}) \end{pmatrix} \begin{pmatrix} h_1 \\ \\ h_2 \end{pmatrix} = \begin{pmatrix} k_1 \\ \\ k_2 \end{pmatrix} $

$d F_p$ es invertible si y sólo si la matriz tiene determinante distinto de cero. Luego $F $ localmente es invertible (cerca de $\vec{p}$ ), quiere decir que podemos despejar las variables independientes.

$ u = f (x, y) \; \; $ entonces $ \; \; x = h (u, v)$

$ v = g (x, y) \; \; $ entonces $ \; \; y = k (u, v)$