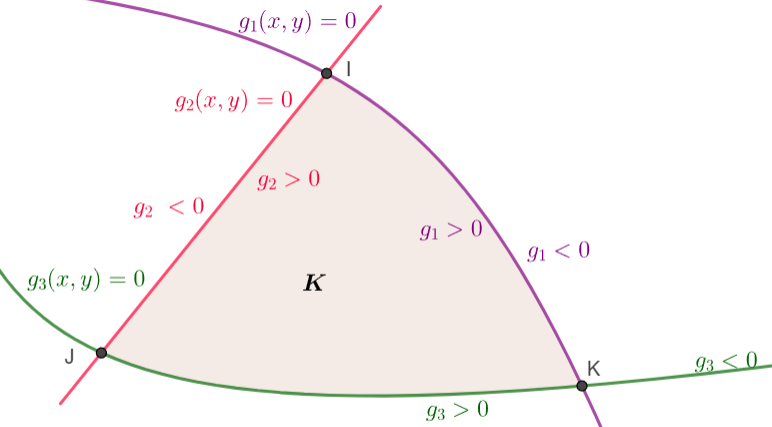
La restricción es de la forma descrita a continuación:

$g_1 (x, y) \geq 0$

$g_2 (x, y) \geq 0$

$\vdots$

$g_n (x, y) \geq 0$

$\mathcal{K} = \big\{ (x, y) \in \mathbb{R}^2 \, \big| \, g_1 (x, y) \geq 0 , g_2 (x, y) \geq 0 , \dots , g_n (x, y) \geq 0 \big\}$, donde $\mathcal{K}$ sea compacto.

$\partial \mathcal{K} \subseteq \mathcal{C}_1 \cap \mathcal{C}_2 \cap \dots \cap \mathcal{C}_n$ donde

$\mathcal{C}_i = \big\{ (x, y) \in \mathbb{R}^2 \, \big| \, g_i (x, y) = 0 \big\}$

Si $\mathcal{K}$ es compacto y $ f $ es continua en todo $\mathcal{K}$ entonces, existen $ (x_0, y_0) , (x_1 , y_1) $ tales que $ f \Big|_{\mathcal{K}} $ alcanza un mínimo global en $( x_0, y_0)$, y un máximo global en $(x_1, y_1).$

Buscamos responder donde se alcanzan. Para ello realizamos lo siguiente:

(*) Buscar si hay puntos críticos de $f$ en el interior de $\mathcal{K}$.

Esos puntos cumplen que:

$\nabla f (x, y) = 0$, es decir que $\dfrac{\partial f}{\partial x} (x, y) = 0$ y $\dfrac{\partial f}{\partial y} (x, y) = 0$. Este es un sistema de dos ecuaciones con dos incógnitas.

(**) Buscar si hay puntos críticos de $f\Big|_{\mathcal{C}_i}$ para alguna de las curvas $\mathcal{C}_i$ definidas por la ecuación $g_i (x, y) = 0$ correspondiente a

$ \nabla f (x, y) = \lambda \nabla g (x, y)$

$g_i (x, y) = 0$; donde estas dos última ecuaciones forman un sistema de 3 x 3.

Esto con cada «lado curvo» de $\mathcal{K}.$

(***) Buscar si en los «vértices» dados por $\mathcal{C}_i \cap \mathcal{C}_j$, $f \Big|_{\mathcal{K}}$ alcanza un valor extremo. El sistema de 2 x 2 dado por

$g_i (x, y) = 0$ y $g_j (x, y) = 0$.

(****) Finalmente considerar los puntos donde $ f $ no sea diferenciable.