Sean:

$ \alpha : I \subset \mathbb{R} \rightarrow \mathbb{R}^n$

$ \beta : I \subset \mathbb{R} \rightarrow \mathbb{R}^n$

dos curvas tales que:

$\alpha (t_0) = \beta (t_0) = \vec{x_0}$;

${\alpha}’ (t_0) \neq \vec{0}$ y

${\beta}’ (t_0) \neq \vec{0}.$

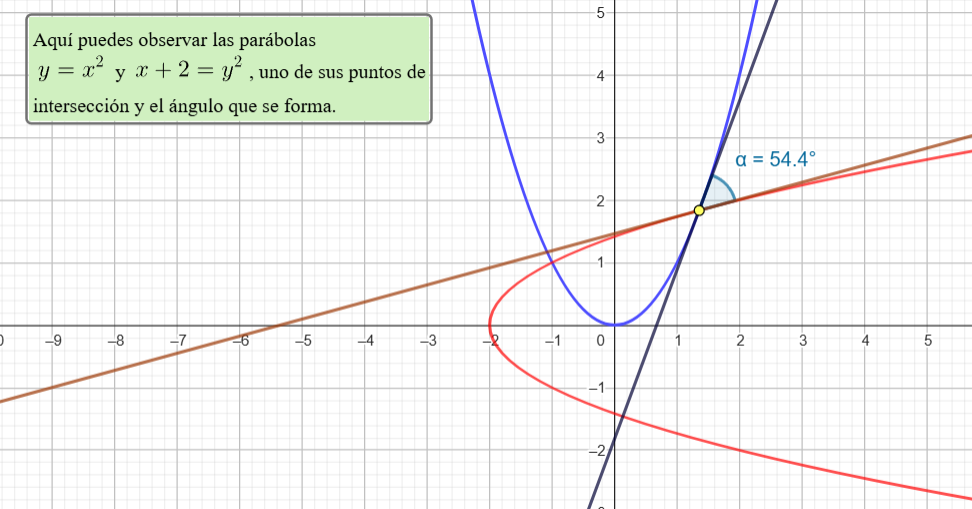
Definimos el ángulo entre las curvas como el ángulo entre los vectores tangentes ${\alpha}’ (t_0)$ y ${\beta}’ (t_0)$

$$ \cos \theta = \dfrac{{\alpha}’ (t_0) \cdot {\beta}’ (t_0)}{ \|{\alpha}’ (t_0)\| \|{\beta}’ (t_0)\|}$$

En el siguiente enlace puedes observar un ejemplo.

https://www.geogebra.org/classic/dwafdmgt

Longitud de arco

Sea $ \alpha : [a, b] \subset \mathbb{R} \rightarrow \mathbb{R}^n$ continua.

Para cada partición del $[a, b]$, $t_0 = a < t_1 < t_2 < \dots < t_n = b$, podemos calcular los puntos $\alpha (t_i).$

Más aún, podemos calcular las longitudes de los segmentos de recta que unen puntos consecutivos de la partición y sumarlos, $$\sum\limits_{i = 1}^n \| \alpha (t_i) – \alpha (t_{i – 1}) \| = \mathcal{L} (C) $$

$\mathcal{L} (C)$ es la longitud de una trayectoria poligonal inscrita en una curva $C.$

Definimos la longitud de arco de $\alpha$ desde $\vec{p} = \alpha (a)$ hasta $\vec{q} = \alpha (b)$ como el supremo del conjunto de números

$$\left\{ \sum\limits_{i = 1}^n \| \alpha (t_i) – \alpha (t_{i – 1}) \|; t_0 = a < t_1 < t_2 < \dots < t_n = b\right\}$$

$$\mathcal{L}(\alpha) := sup \{ \mathcal{L}(C) \}$$

Observación:

ésta definición se extiende a espacios métricos $(\mathcal{X}, d)$, con

$ \alpha : I \subset \mathbb{R} \rightarrow \mathcal{X}$

$$ \mathcal{L}(C)= \sum\limits_{i = 1}^n d \left( \alpha (t_{i-1}), \alpha (t_i) \right)$$

$$\mathcal{L}(\alpha) := sup \{ \mathcal{L}(C) \}$$