Archivo de la etiqueta: variables aleatorias

Probabilidad I: Funciones de Distribución de Probabilidad

Por Octavio Daniel Ríos García

Deja un comentario

Introducción

Una vez que hemos introducido el concepto de variable aleatoria, nos toca ver qué nuevas definiciones surgen a partir de este. Un primer concepto que surge es la función de distribución. A grandes rasgos, dado un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$, en la entrada anterior vimos que una función $X\colon\Omega\to\RR$ debe de satisfacer que para cualquier $x \in \RR$, $X^{-1}[(-\infty, x]]$ es un evento de $\Omega$. Básicamente, esta condición era suficiente para concluir que para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$. En otras palabras, la imagen inversa de cualquier evento de $\RR$ es un evento de $\Omega$.

De manera similar, lo que haremos será definir la probabilidad de los eventos de la forma $(X \leq x)$, con $x \in \RR$. No lo veremos aquí (porque no tenemos las herramientas suficientes para hacerlo), pero resulta que asignarle probabilidad a esos eventos captura toda la información relevante sobre una variable aleatoria. Esto nos permitirá prescindir por completo de muchos detalles de la variable aleatoria, y centrar nuestra atención en el conjunto de valores que puede tomar.

Funciones de distribución de probabilidad

De manera general, existe un tipo de función que nos va a interesar a partir de ahora, que corresponde a las funciones de distribución de probabilidad. Estas se definen como sigue.

Definición. Sea $F\colon\RR\to\RR$ una función. Diremos que $F$ es una función de distribución de probabilidad si:

  1. $F$ es no-decreciente. Esto es, para cada $a, b \in \RR$, si $a < b$ entonces $F(a) \leq F(b)$.
  2. $F$ es continua por la derecha. Es decir, para cada $a \in \RR$ se cumple que\[ \lim_{x\to a^{+}} F(x) = F(a). \]
  3. Se cumple que\[ \lim_{x\to\infty} F(x) = 1 \quad\text{y}\quad \lim_{x\to -\infty} F(x) = 0. \]

Una función no requiere de ningún contexto adicional para considerarse una función de distribución de probabilidad. Es decir, para que una función $F\colon\RR\to\RR$ sea considerada una función de distribución de probabilidad, simplemente debe de ser no-decreciente, continua por la derecha y sus límites a $\infty$ y $-\infty$ deben de ser $1$ y $0$, respectivamente.

Ejemplo 1. Sean $a, b \in \RR$ tales que $a < b$. La función $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 0 & \text{si $x < a$,} \\[1em] \cfrac{x − a}{b − a} & \text{si $a \leq x \leq b$,} \\[1em] 1 & \text{si $b < x$.} \end{cases} \]

es no-decreciente, continua por la derecha y sus límites a $\infty$ y $-\infty$ son $1$ y $0$, así que es una función de distribución de probabilidad. Gráficamente, se ve como sigue.

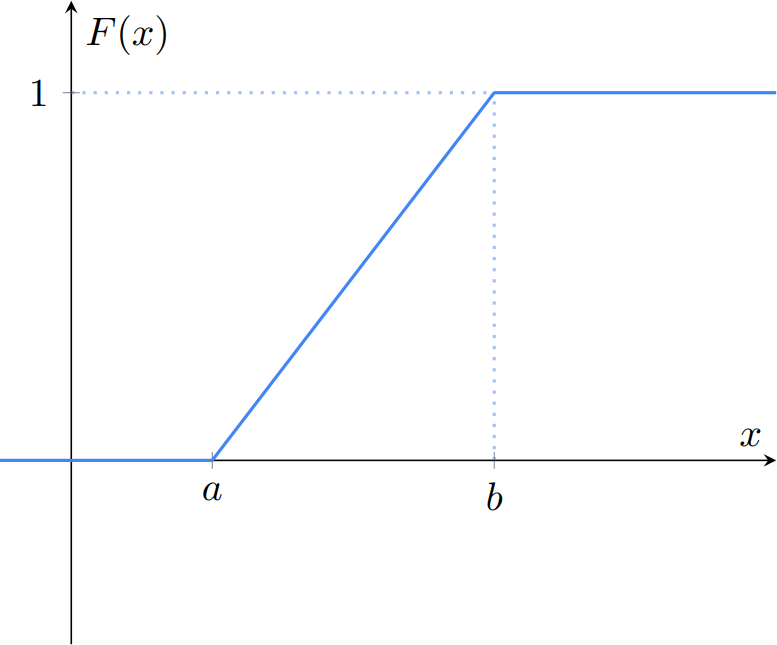
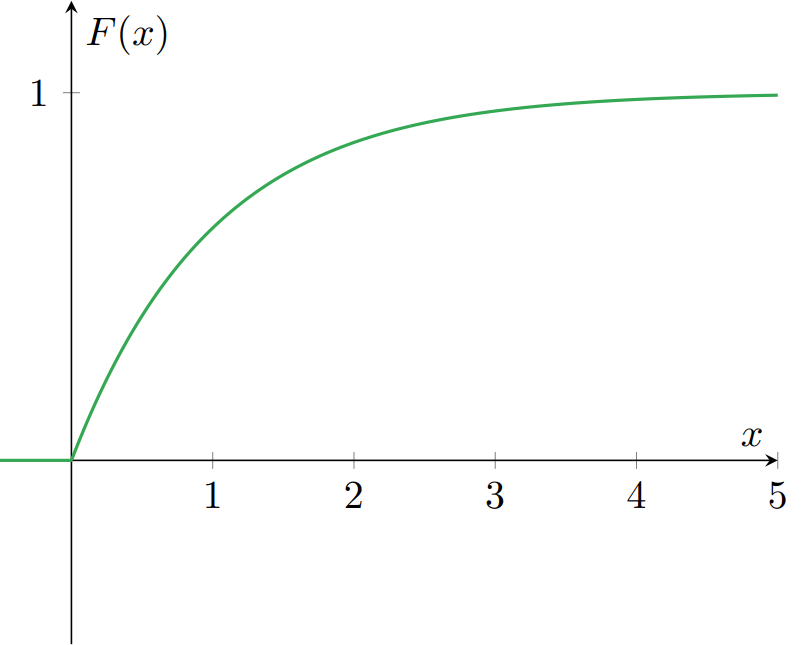
Figura. Gráfica de la función de distribución de probabilidad expuesta en este ejemplo.

Ejemplo 2. Sea $\lambda \in \RR$ tal que $\lambda > 0$. La función $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] 1 − e^{-\lambda x} & \text{si $x \geq 0$.} \end{cases} \]

es una función de distribución de probabilidad. Gráficamente:

Figura. Gráfica de la función de distribución de probabilidad de este ejemplo.

Función de distribución de una variable aleatoria

Dada cualquier variable aleatoria $X$ sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$, hay una función muy importante asociada a $X$: su función de distribución, definida como sigue.

Definición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sea $X\colon\Omega\to\RR$ una variable aleatoria. La función de distribución de $X$ es la función $F_{X}\colon\RR\to[0,1]$ dada por

\[ F_{X}(x) = \Prob{\{\, \omega\in\Omega \mid X(\omega) \leq x \,\}} = \Prob{X \leq x}, \quad \text{para cada $x \in \RR$}. \]

$F_{X}$ también es llamada la función de distribución acumulada de $X$, que en inglés se abrevia como CDF (cumulative distribution function).

Es decir, dada una variable aleatoria $X$, su función de distribución devuelve la probabilidad de que $X$ sea menor o igual a $x$, para cada $x \in\RR$. Como seguramente ya sospechas por el nombre de $F_{X}$, resulta que $F_{X}$ es una función de distribución de probabilidad. Este hecho es demostrado en el siguiente teorema.

Teorema. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sea $X\colon\Omega\to\RR$ una variable aleatoria. Entonces $F_{X}\colon\RR\to[0,1]$ es una función de distribución de probabilidad.

Demostración. De acuerdo con la definición, para demostrar que $F_{X}\colon\RR\to\RR$ es una función de distribución de probabilidad, tenemos que demostrar 3 cosas:

  1. $F_{X}$ es no-decreciente: para cada $a, b \in \RR$, si $a < b$ entonces $F_{X}(a) \leq F_{X}(b)$.
  2. $F_{X}$ es continua por la derecha: que para cada $a \in \RR$ se cumple que\[ \lim_{x\to a^{+}} F_X(x) = F_{X}(a). \]
  3. Se cumple que\[ \lim_{x\to\infty} F_{X}(x) = 1 \quad\text{y}\quad \lim_{x\to -\infty} F_{X}(x) = 0. \]

Veamos que se cumple 1. Sean $a, b \in \RR$ tales que $a < b$. Ahora, observa que $(a, b] = (-\infty, b] \smallsetminus (-\infty, a]$, por lo que

\begin{align*} \Prob{X^{-1}[(a, b]]} &= \Prob{X^{-1}[(-\infty, b] \smallsetminus (-\infty, a]]} \\[0.5em] &= \Prob{X^{-1}[(-\infty, b]] \smallsetminus X^{-1}[(-\infty, a]]}. \end{align*}

Como $a < b$, se cumple que $(-\infty, a] \subseteq (-\infty, b]$, por lo que

\[ X^{-1}[(-\infty, a]] \subseteq X^{-1}[(-\infty, b]], \]

así que $\Prob{X^{-1}[(-\infty, b]] \smallsetminus X^{-1}[(-\infty, a]]} = \Prob{X^{-1}[(-\infty, b]]} − \Prob{X^{-1}[(-\infty, a]]}$. En consecuencia, tenemos que

\begin{align*} \Prob{X^{-1}[(a, b]]} &= \Prob{X^{-1}[(-\infty, b]]} − \Prob{X^{-1}[(-\infty, a]]} \\[0.5em] &= \Prob{X \leq b} − \Prob{X \leq a} \\[0.5em] &= F_{X}(b) − F_{X}(a). \end{align*}

Recuerda que $\mathbb{P}$ es una medida de probabilidad, por lo que $\Prob{X^{-1}[(a, b]]} \geq 0$; que implica $F_{X}(b) − F_{X}(a) \geq 0$, o equivalentemente, que $F_{X}(b) \geq F_{X}(a)$. En conclusión, para cualesquiera $a, b \in \RR$ tales que $a < b$, se cumple que $F_{X}(a) \leq F_{X}(b)$, que es justamente lo que queríamos demostrar. Por lo tanto, $F_{X}$ es una función no-decreciente.

Para demostrar 2, sea $(x_{n})_{n\in\mathbb{N}^{+}} \subseteq \RR$ una sucesión monótona decreciente de números reales tal que su límite es $0$. Es decir, $x_{1} > x_{2} > x_{3} > \cdots$ y

\[ \lim_{n\to\infty} x_{n} = 0. \]

Ahora, sea $a \in \RR$. Definimos la sucesión de eventos $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$ tal que para cada $n \in \mathbb{N}^{+}$, $A_{n} = ( X \leq a + x_{n} )$. De este modo, se tiene que

\[ \bigcap_{n=1}^{\infty} A_{n} = (X \leq a), \]

pues la sucesión $(x_{n})_{n\in\mathbb{N}^{+}}$ converge a $0$. Ahora, por el teorema de continuidad de la probabilidad, tenemos que

\[ F_{X}(a) = \Prob{X \leq a} = \Prob{\bigcap_{n=1}^{\infty} A_{n}} = \lim_{n\to\infty} \Prob{A_{n}} = \lim_{n\to\infty} \Prob{X \leq a + x_{n}} = \lim_{n\to\infty} F_{X}(a + x_{n}), \]

es decir, $\lim_{n\to\infty} F_{X}(a + x_{n}) = F_{X}(a)$, para cualquier $a \in \RR$ y cualquier sucesión monótona decreciente $(x_{n})_{n\in\mathbb{N}^{+}}$. Por ello, se puede concluir que $F_{X}$ es una función continua por la derecha.

Finalmente, en 3 demostraremos que el límite de $F_{X}(x)$ cuando $x\to\infty$ es $1$. La demostración del otro límite es muy parecida. Sea $(x_{n})_{n\in\mathbb{N}^{+}} \subseteq \RR$ una sucesión de números reales tal que $x_{1} \leq x_{2} \leq x_{3} \leq \cdots$ y $\lim_{n\to\infty} x_{n} = \infty$. Para cada $n \in \mathbb{N}^{+}$ definimos

\[ A_{n} = (X \leq x_{n}) = X^{-1}[(-\infty, x_{n}]]. \]

De esta forma, tenemos que $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$ es una sucesión creciente de eventos, pues observa que $A_{1} \subseteq A_{2} \subseteq A_{3} \subseteq \cdots$ De este modo, como supusimos que $(x_{n})_{n\in\mathbb{N}^{+}}$ es una sucesión que diverge a $\infty$, se tiene que

\[ \bigcup_{n=1}^{\infty} A_{n} = \bigcup_{n=1}^{\infty}(X \leq x_{n}) = \bigcup_{n=1}^{\infty}X^{-1}[(-\infty, x_{n}]] = X^{-1}{\left[ \bigcup_{n=1}^{\infty} (-\infty, x_{n}] \right]} = X^{-1}[\RR] = \Omega. \]

Ahora, aplicando el teorema de la continuidad de la probabilidad a $\{ A_{n}\}_{n\in\mathbb{N}^{+}}$ y usando que la sucesión $(x_{n})_{n\in\mathbb{N}^{+}}$ es divergente, tenemos que

\begin{align*} \lim_{x\to\infty} F_{X}(x) &= \lim_{n\to\infty} F_{X}(x_{n}) \\ &= \lim_{n\to\infty}\Prob{X \leq x_{n}} \\ &= \lim_{n\to\infty}\Prob{A_{n}} \\ &= \Prob{\bigcup_{n=1}^{\infty} A_{n}} \\ &= \Prob{\Omega} \\ &= 1. \end{align*}

En conclusión, tenemos que

\[ \lim_{x\to\infty} F_{X}(x) = 1, \]

que es justamente lo que queríamos demostrar. La demostración de que el límite a $-\infty$ de $F_{X}$ es $0$ se obtiene de manera casi análoga, pero la familia de eventos que se plantea es decreciente, y se utiliza el teorema de continuidad de la probabilidad para ese caso.

$\square$

Partiendo de una función de distribución de probabilidad

Por el teorema anterior, vimos que la función de distribución de cualquier variable aleatoria es también una función de distribución de probabilidad. Es decir, que si tienes un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$, la función de distribución de $X$, $F_{X}\colon\RR\to[0,1]$, es una función de distribución de probabilidad.

Por otro lado, ahora imagina que te encuentras con una función $F\colon\RR\to\RR$ que es una función de distribución de probabilidad. No obstante, observa que no sabes nada más sobre esta función. Es decir, no hay ninguna variable aleatoria ni un espacio de probabilidad a la vista… ¿Será posible que $F$ provenga de alguna variable aleatoria $X$ definida sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$?

En otras palabras: dada $F\colon\RR\to\RR$ una función de distribución de probabilidad, ¿siempre existen un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$ tal que $F$ es la función de distribución de $X$? ¡La respuesta es que sí! A grandes rasgos, $F$ define la probabilidad de los eventos de la forma $(-\infty, x]$, para cada $x \in \RR$. Esto resulta suficiente para definir por completo la medida de probabilidad inducida por una variable aleatoria $X$… pero, ¿cuál variable aleatoria $X$? De manera canónica, siempre puede utilizarse la variable aleatoria identidad sobre $\Omega = \RR$, que es la función $X\colon\RR\to\RR$ tal que para cada $\omega\in\RR$, $X(\omega) = \omega$. De este modo, la medida de probabilidad inducida por $X$ es la misma que la medida en el dominio de $X$, que en este caso es $\RR$ con $\mathscr{B}(\RR)$ como σ-álgebra, y usando la medida determinada por $F$.

¡CUIDADO! Esto NO significa que todas las variables aleatorias son simplemente la función identidad. Lo que significa es que siempre que tengas una función de distribución de probabilidad $F\colon\RR\to\RR$, está garantizado que existen un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$ de tal forma que $F$ es la función de distribución de $X$. La existencia está garantizada porque, al menos, siempre se puede usar la función identidad de $\RR$ en $\RR$ como variable aleatoria, pero puede haber otras distintas cuya función de distribución también es $F$.

Los siguientes ejemplos son largos, pero capturan muchas de las ideas vistas hasta ahora sobre variables aleatorias. Además, en conjunto, estos dos ejemplos exhiben lo que comentamos en el párrafo anterior.

Ejemplo 3. Sea $\Omega = \{ 0, 1\}^{3}$. Es decir, $\Omega$ es el conjunto

\[ \Omega = \{ (0,0,0), (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0), (1,1,1) \}. \]

$\Omega$ puede pensarse como el espacio muestral de un experimento aleatorio en el que se hacen $3$ ensayos de un experimento aleatorio que tiene dos resultados posibles: éxito o fracaso. Por ejemplo, el lanzamiento de una moneda («águila» o «sol»). Tomaremos como σ-algebra de $\Omega$ a $\mathscr{P}(\Omega)$, la potencia de $\Omega$.

Sea $p \in \RR$ tal que $p \in [0,1]$. Plantearemos una medida de probabilidad tal que los $3$ ensayos son independientes. Para ello, para cada $k \in \{1,2,3\}$ planteamos los eventos

  • $A_{k}$: el evento de que el $k$-ésimo ensayo sea un éxito. Es decir, $A_{k}$ es el evento\[ A_{k} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{k} = 1 \,\}. \]
  • $B_{k}$: el evento de que el $k$-ésimo ensayo sea un fracaso. Es decir, $B_{k}$ es el evento\[ B_{k} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{k} = 0 \,\}. \]

Observa que para cada $k \in \{1,2,3\}$ se cumple que $B_{k} = A_{k}^{\mathsf{c}}$. Por ejemplo, $A_{2}$ es el evento

\[ A_{2} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{2} = 1 \,\} = \{ (0,1,0), (0,1,1), (1,1,0), (1,1,1) \} \]

Comenzamos a definir la medida de probabilidad $\mathbb{P}\colon\mathscr{P}(\Omega)\to\RR$ como sigue: para cada $k \in \{1,2,3\}$ definimos

\[ \Prob{A_{k}} = p, \]

\[ \Prob{B_{k}} = 1 − p, \]

y pedimos que $\mathbb{P}$ sea tal que los eventos $A_{1}$, $A_{2}$ y $A_{3}$ son independientes. En consecuencia, se cumple lo siguiente

\begin{align} \Prob{A_{1} \cap A_{2} \cap A_{3}} &= \Prob{A_{1}}\Prob{A_{2}}\Prob{A_{3}} = p^{3} \\[1em] \Prob{B_{1} \cap A_{2} \cap A_{3}} &= \Prob{B_{1}}\Prob{A_{2}}\Prob{A_{3}} = (1 − p)p^{2} = p^{2}(1 − p) \\[1em] \Prob{A_{1} \cap B_{2} \cap A_{3}} &= \Prob{A_{1}}\Prob{B_{2}}\Prob{A_{3}} = p(1 − p)p = p^{2}(1 − p) \\[1em] \Prob{A_{1} \cap A_{2} \cap B_{3}} &= \Prob{A_{1}}\Prob{A_{2}}\Prob{B_{3}} = p^{2}(1 − p), \\[1em] \Prob{B_{1} \cap B_{2} \cap A_{3}} &= \Prob{B_{1}}\Prob{B_{2}}\Prob{A_{3}} = (1 − p)^{2}p = p(1 − p)^{2}, \\[1em] \Prob{B_{1} \cap A_{2} \cap B_{3}} &= \Prob{B_{1}}\Prob{A_{2}}\Prob{B_{3}} = (1− p)p(1− p) = p(1 − p)^{2}, \\[1em] \Prob{A_{1} \cap B_{2} \cap B_{3}} &= \Prob{A_{1}}\Prob{B_{2}}\Prob{B_{3}} = p(1 − p)^{2}, \\[1em] \Prob{B_{1} \cap B_{2} \cap B_{3}} &= \Prob{B_{1}}\Prob{B_{2}}\Prob{B_{3}} = (1 − p)^{3}. \\[1em] \end{align}

De hecho, observa que estas condiciones son suficientes para definir la probabilidad de cada resultado, y así, la de cada evento $A \in \mathscr{P}(\Omega)$. Por ejemplo, nota que

\[ A_{1} \cap A_{2} \cap A_{3} = \{ \, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{1} = 1 \land \omega_{2} = 1 \land \omega_{3} = 1 \, \} = \{ (1,1,1) \}, \]

y por lo anterior, $\Prob{A_{1} \cap A_{2} \cap A_{3}} = p^{3}$. Por lo tanto, se concluye que

\[ \Prob{\{(1,1,1)\}} = p^{3}. \]

Los $8$ elementos de $\Omega$ pueden verse como las intersecciones de las identidades $(1)$ a $(8)$, así que la probabilidad de cada uno está determinada por cada una de esas igualdades. Por ejemplo, además de la anterior ($\Prob{\{(1,1,1)\}} = p^{3}$), observa que

\[ A_{1} \cap B_{2} \cap B_{3} = \{ \, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{1} = 1 \land \omega_{2} = 0 \land \omega_{3} = 0 \, \} = \{ (1,0,0) \}, \]

por lo que $\Prob{\{(1,0,0)\}} = p(1−p)^{2}$. Ahora, presta atención a los exponentes de $p$ y de $1−p$ en estas probabilidades, y compáralos con el número de $1$’s y $0$’s de las ternas ordenadas. ¿Qué puedes observar? Resulta que el exponente de la $p$ es el número de $1$’s, es decir, el número de éxitos. Por otro lado, el exponente del $1−p$ es el número de $0$’s, es decir, el número de fracasos.

Ahora, para cada $\mathbf{a} \in \Omega$, $\mathbf{a}$ puede escribirse como $\mathbf{a} = (a_{1}, a_{2}, a_{3})$, con $a_{1}$, $a_{2}$, $a_{3} \in \{0,1\}$. En consecuencia, el número de éxitos en la terna $\mathbf{a}$ puede escribirse como

\[ {\lVert \mathbf{a} \rVert}_{1} = {\left\lVert (a_{1}, a_{2}, a_{3}) \right\rVert}_{1} = |a_{1}| + |a_{2}| + |a_{3}|. \]

Por el contrario, el número de fracasos en la terna $\mathbf{a}$ puede escribirse como

\[ 3 − {\lVert \mathbf{a} \rVert}_{1} = 3 − {\left\lVert (a_{1}, a_{2}, a_{3}) \right\rVert}_{1} = 3 − (|a_{1}| + |a_{2}| + |a_{3}|). \]

De este modo, para cada $\mathbf{a} \in \Omega$, se tiene que

\[ \Prob{\{\mathbf{a}\}} = p^{{\lVert \mathbf{a} \rVert}_{1}} (1−p)^{3 − {\lVert \mathbf{a}\rVert}_{1}}. \]

Por esta razón, definimos a la medida de probabilidad $\mathbb{P}\colon\mathscr{P}(\Omega) \to \RR$ dada por

\[ \Prob{A} = \sum_{\mathbf{a}\in A} p^{{\lVert \mathbf{a} \rVert}_{1}} (1−p)^{3 − {\lVert \mathbf{a}\rVert}_{1}}, \quad \text{para cada $A \in \mathscr{P}(\Omega)$.}\]

Ahora, definimos a la variable aleatoria $X\colon\Omega\to\RR$ como sigue. Para cada $\mathbf{a}\in\Omega$, se define

\[ X(\mathbf{a}) = \lVert \mathbf{a} \rVert_{1}, \]

por lo que si $\mathbf{a} = (a_{1}, a_{2}, a_{3})$, se tiene que

\[ X(\mathbf{a}) = |a_{1}| + |a_{2}| + |a_{3}|. \]

Por ejemplo, $X(1,0,1) = 1 + 0 + 1 = 2$, y $X(1,1,1) = 1+1+1 = 3$. Es decir, $X$ contabiliza el número de éxitos en los $3$ ensayos. Observa que el conjunto de valores que puede tomar $X$ es $\{ 0, 1, 2, 3 \}$. Obtengamos la probabilidad de que $X$ tome cada uno de estos valores.

\begin{align*} \Prob{X = 0} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 0 \,\}} &= \Prob{\{ (0,0,0) \}} \\[0.5em] &= (1−p)^{3}, \\[1.5em] \Prob{X = 1} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 1 \,\}} &= \Prob{\{ (1,0,0), (0,1,0), (0,0,1) \}} \\[0.5em] &= p(1−p)^{2} + p(1−p)^{2} + p(1−p)^{2} \\[0.5em] &= 3p(1−p)^{2}, \\[1.5em] \Prob{X = 2} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 2 \,\}} &= \Prob{\{ (1,1,0), (1,0,1), (0,1,1) \}} \\[0.5em] &= p^{2}(1−p) + p^{2}(1−p) + p^{2}(1−p) \\[0.5em] &= 3p^{2}(1−p), \\[1.5em] \Prob{X = 3} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 3 \,\}} &= \Prob{\{ (1,1,1) \}} \\[0.5em] &= p^{3}. \end{align*}

Ahora obtengamos la función de distribución de $X$. Esto es,

\[ F_{X}(x) = \Prob{X \leq x}. \]

Primero, observa que para cada $x \in (-\infty, 0)$ se tiene que $F_{X}(x) = 0$, pues la variable aleatoria no toma valores negativos. Después,

\[ F_{X}(0) = \Prob{X \leq 0} = \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 0 \,\}} = \Prob{\{ (0,0,0) \}} = (1−p)^{3}. \]

Por otro lado, para cada $x \in (0,1)$, observa que

\[ F_{X}(x) = \Prob{X \leq x} = \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq x \,\}} = \Prob{\{ (0,0,0) \}}. \]

porque el único $\omega \in \Omega$ que hace que $X(\omega) \leq x$ es $\omega = (0,0,0)$, para todos los demás, $X(\omega)$ vale al menos $1$, que es mayor a $x$. Luego, tenemos que

\begin{align*} F_{X}(1) = \Prob{X \leq 1} &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 1 \,\}} \\[0.5em] &= \Prob{\{ (0,0,0), (0,0,1), (0,1,0), (1,0,0) \}} \\[0.5em] &= (1−p)^{3} + 3p(1−p)^{2}, \end{align*}

Observa que ahí se acumularon los elementos de $\Omega$ que hacen que $X(\omega) = 0$ y $X(\omega) = 1$, pues son todos los valores que toma la variable aleatoria que son menores o iguales a $1$.

Después, para cada $x\in(1,2)$, los $\omega\in\Omega$ que hacen que $X(\omega) \leq x$ son los mismos que en el caso anterior, por lo que $F_{X}(x) = F_{X}(1)$. Continuando de esta manera, se llega a que

\begin{align*} F_{X}(2) &= (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p), \\[0.5em] F_{X}(x) &= F_{X}(2) & \text{para cada $x \in (2,3)$,} \\[0.5em] F_{X}(3) &= (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) + p^{3}, \\[0.5em] F_{X}(x) &= F_{X}(3) & \text{para cada $x \in (3,\infty)$.} \end{align*}

Observa que la expresión para $F_{X}(3)$ corresponde a $(p + (1−p))^{3}$, por el teorema del binomio. En consecuencia, $F_{X}(3) = (p + (1−p))^{3} = 1^3 = 1$. De este modo, obtenemos que la función de distribución de $X$ es la función dada por

\[ F_{X}(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] (1−p)^{3} & \text{si $0 \leq x < 1$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} & \text{si $1 \leq x < 2$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) & \text{si $2 \leq x < 3$,} \\[1em] 1 & \text{si $3 \leq x$.} \end{cases} \]

Nota que a pesar de ser una función con discontinuidades (es una función escalonada), $F_{X}$ sí es continua por la derecha. Observa que también es no-decreciente, y sus límites a $-\infty$ y a $\infty$ son $0$ y $1$, respectivamente; algo que ya esperábamos por el teorema demostrado en esta entrada.

Figura. Gráfica de la función $F_{X}$. Es una función escalonada, continua por la derecha. Sus discontinuidades las representamos como círculos sin relleno. Para hacer la gráfica, utilizamos el valor $p = \frac{1}{2}$.

Ejemplo 4. Ahora sea $F\colon\RR\to\RR$ la siguiente función de distribución de probabilidad:

\[ F(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] (1−p)^{3} & \text{si $0 \leq x < 1$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} & \text{si $1 \leq x < 2$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) & \text{si $2 \leq x < 3$,} \\[1em] 1 & \text{si $3 \leq x$.} \end{cases} \]

¡Es la función de distribución de la variable aleatoria $X$ del ejemplo pasado! Sin embargo, nota que aquí te la estamos dando sin ninguna información sobre el espacio de probabilidad subyacente, ni sobre la variable aleatoria involucrada. En primer lugar, ya tenemos garantizado que existe el espacio de probabilidad $(\{0,1\}^{3}, \mathscr{P}(\{0,1\}^{3}), \mathbb{P})$ y la variable aleatoria $X\colon\{0,1\}^{3}\to\RR$ dada por $X(\omega) = {\lVert \omega \rVert}_{1}$, para cada $\omega\in\{0,1\}^{3}$ de tal forma que $F$ es la función de distribución de $X$.

No obstante, observa que podemos definir otra variable aleatoria que resulta en la misma función de distribución. Para ello, toma a $(\RR, \mathscr{B}(\RR), \mathbb{P})$, donde $\mathbb{P}$ es la medida de probabilidad $\mathbb{P}\colon\mathscr{B}(\RR)\to\RR$ definida como sigue: para cada $x\in\RR$, definimos

\[ \Prob{(-\infty, x]} = F(x). \]

Ojo: Esto define la probabilidad de los elementos de $\mathscr{B}(\RR)$ (que son eventos) que tienen la forma $(-\infty, x]$, para cada $x \in \RR$. A su vez, esto define la probabilidad de los eventos de la forma $(a, b]$, para cada $a$, $b \in \RR$ tales que $a < b$, que es

\[ \Prob{(a,b]} = F(b) − F(a), \]

que se puede extender de manera única a una medida sobre todo $\mathscr{B}(\RR)$. Esto es algo que puede demostrarse, pero carecemos de las herramientas para hacerlo en este curso. De cualquier modo, la variable aleatoria que utilizamos en este caso es $Y\colon\RR\to\RR$, la función identidad, dada por

\[ Y(\omega) = \omega, \quad \text{para cada $\omega \in \RR$.} \]

De este modo, se tiene que

\begin{align*} (Y \leq y) &= \{ \, \omega \in \RR \mid Y(\omega) \leq y \, \} \\[0.5em] &= \{ \, \omega \in \RR \mid \omega \leq y \, \} \\[0.5em] &= (-\infty, y], \end{align*}

y por lo tanto, para cada $y \in \RR$,

\[ F_{Y}(y) = \Prob{Y \leq y} = \Prob{(-\infty, y]} = F(y), \]

por lo que la función de distribución de $Y$ es precisamente la función de distribución de probabilidad que escogimos al comenzar este ejemplo. De este modo, $Y$ es una variable aleatoria que puede tomar los valores $0$, $1$, $2$ y $3$… ¡con las mismas probabilidades que la variable aleatoria $X$ del ejemplo pasado! Sin embargo, ¡los espacios de probabilidad sobre los que estas están definidas son completamente distintos! Esto exhibe que lo más importante de una variable aleatoria es su función de distribución, pues esta determina los valores que puede tomar, y la probabilidad con la que los toma. Es decir, la función de distribución caracteriza el comportamiento probabilístico de una variable aleatoria.

¡Presta mucha atención a los últimos dos ejemplos! La conclusión es que el espacio de probabilidad que subyace a una variable aleatoria realmente no importa. Por ello, en muchos libros de probabilidad (y en este mismo curso), no le prestan atención a esto. Comúnmente, te dan una función $F$ que es una función de distribución de probabilidad, y te dicen «sea $X$ una variable aleatoria con distribución $F$». Con eso es suficiente, pues $F$ determina las probabilidades de todos los eventos que involucran a $X$, sin importar quiénes son $X$ y el espacio de probabilidad sobre el que ésta se define.

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

  1. Determina si la función $F\colon\RR\to\RR$ dada por\[F(x) = \begin{cases} 0 & \text{si $x \leq -1$,} \\[0.5em] \frac{1}{2}(x+1)^2 & \text{si $-1 < x \leq 0$,} \\[0.5em] 1 − \frac{1}{2}(1 − x)^{2} & \text{si $0 < x < 1$,} \\[0.5em] 1 &\text{si $x \geq 1$} \end{cases} \]es una función de distribución de probabilidad. Utiliza su gráfica para auxiliarte, en caso de que lo necesites.
  2. Demuestra que el límite a $-\infty$ de la función de distribución de una variable aleatoria es $0$ Sugerencia: Revisa la demostración de la propiedad 3 que vimos en el teorema de esta entrada.
  3. ¿Podrías idear más variables que tengan la misma función de distribución del Ejemplo 3? Por ejemplo, si \(\Omega_{2} = \{0,2\}^{3}\), decimos que \(2\) representa éxito; y definimos \(Z\colon\Omega_{2}\to\RR\) como la función dada por\begin{align*} Z(\omega_{1}, \omega_{2}, \omega_{3}) &= \frac{\omega_{1} + \omega_{2} + \omega_{3}}{2} & \text{para cada \((\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega_{2}\),} \end{align*}¿tiene \(Z\) la misma distribución que la \(X\) del Ejemplo 3?

Más adelante…

Lo siguiente que haremos en el curso es ver los dos tipos de variables aleatorias más importantes que hay, las discretas y las continuas. A grandes rasgos, las discretas son aquellas que pueden tomar una cantidad a lo más numerable de valores distintos, mientras que las continuas son aquellas que pueden tomar una cantidad no-numerable de valores. Es decir, pueden tomar valores en un conjunto cuya cardinalidad es igual a la de $\RR$. En la siguiente entrada abordaremos las particularidades de las variables aleatorias discretas.

Entradas relacionadas

Probabilidad I: Variables Aleatorias

Por Octavio Daniel Ríos García

Deja un comentario

Introducción

En la entrada pasada concluimos la primera unidad del curso. Con esto finaliza nuestro estudio general de las medidas de probabilidad. Por otro lado, el contenido de la segunda unidad está enfocado el estudio de las variables aleatorias y sus propiedades.

En esta entrada abordaremos el concepto de variable aleatoria. A grandes rasgos, una variable aleatoria es una función que actúa sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y devuelve valores numéricos. Sin embargo, no cualquier función puede considerarse una variable aleatoria. Básicamente, una función será una variable aleatoria si algunas de sus imágenes inversas son eventos de $\Omega$. Esto garantizará que se puede calcular la probabilidad de sus valores, y por tanto, podremos calcular la probabilidad de que la variable aleatoria tome valores específicos.

Ideas preliminares

Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Es posible que nos interese algún valor numérico asociado a los resultados del experimento en cuestión. Por ejemplo, considerando el experimento de lanzar una moneda $4$ veces de manera equiprobable, sabemos que su espacio muestral es

\[ \Omega = \begin{Bmatrix} \mathrm{AAAA}, & \mathrm{AAAS}, & \mathrm{AASA}, & \mathrm{ASAA}, \\ \mathrm{SAAA}, & \mathrm{AASS}, & \mathrm{ASAS}, & \mathrm{SAAS}, \\ \mathrm{ASSA}, & \mathrm{SASA}, & \mathrm{SSAA}, & \mathrm{SSSA}, \\ \mathrm{SSAS}, & \mathrm{SASS}, & \mathrm{ASSS}, & \mathrm{SSSS} \end{Bmatrix}. \]

y tomamos a $\mathscr{P}(\Omega)$ como σ-álgebra, y como medida a la medida de probabilidad clásica. Una variable asociada a este experimento es la cantidad de águilas que salieron en los $4$ lanzamientos. Esto podríamos definirlo como una función $X\colon \Omega \rightarrow \RR$, tal que para cada $\omega \in \Omega$ se define

\[ X(\omega) = \text{# de $\mathrm{A}$’s en $\omega$}. \]

De este modo, se tiene que

\begin{align*} &X(\mathrm{AAAS}) = 3, \\ &X(\mathrm{ASAS}) = 2, \end{align*}

\begin{align*} &X(\mathrm{ASSS}) = 1, \\ &X(\mathrm{AAAA}) = 4, \end{align*}

etcétera. Al ser una función, $X$ tiene todas las cualidades y propiedades de una función que viste en álgebra superior. En particular, hay un concepto que nos interesa mucho: la imagen inversa de cada uno de los valores que toma $X$. Como recordatorio, dado $B \subseteq \RR$, la imagen inversa de $B$ bajo $X$ es el conjunto

\[ X^{-1}[B] = \{ \, \omega \in \Omega \mid X(\omega) \in B \, \}. \]

Cuando $B$ es un conjunto de la forma $B = \{ x \}$, con $x \in \RR$, se tiene que

\[ X^{-1}[\{x \}] = \{ \, \omega \in \Omega \mid X(\omega) = x \, \}. \]

Por ejemplo, para la función $X$ como la definimos, podemos observar que

\[ X^{-1}[\{ 2 \}] = \{ \, \omega \in \Omega \mid X(\omega) = 2 \, \} = \{ \mathrm{AASS}, \mathrm{ASAS}, \mathrm{SAAS}, \mathrm{ASSA}, \mathrm{SASA}, \mathrm{SSAA} \}. \]

Ahora, observa que $X^{-1}[{ 2 }] \in \mathscr{P}(\Omega)$, por lo que le podemos asignar una probabilidad. En consecuencia, se tiene que

\begin{align*} \Prob{X^{-1}[\{ 2 \}]} = \Prob{\{ \, \omega \in \Omega \mid X(\omega) = 2 \, \}} &= \frac{|\{ \mathrm{AASS}, \mathrm{ASAS}, \mathrm{SAAS}, \mathrm{ASSA}, \mathrm{SASA}, \mathrm{SSAA} \}|}{|\Omega|} \\ &= \frac{6}{16} \\[1.15em] &= 0.375. \end{align*}

Gracias a esto, podemos decir que «la probabilidad de que $X$ tome el valor $2$ es $\frac{6}{16} = 0.375$». Es decir, le podemos asignar probabilidad a los posibles resultados de $X$. Una notación muy frecuente en el contexto de la probabilidad es la siguiente: usaremos $(X \in B)$ para denotar a $\{ \, \omega \in \Omega \mid X(\omega) \in B \,\} = X^{-1}[B]$, de tal forma que

\[ \Prob{\{ \, \omega \in \Omega \mid X(\omega) \in B \,\}} = \Prob{X \in B}. \]

Del mismo modo, cuando $B = \{x\}$, con $x \in \RR$, se adopta la notación $( X = x )$ para denotar al conjunto $\{ \, \omega \in \Omega \mid X(\omega) = x \,\} = X^{-1}{\left[\{ x \}\right]}$, de tal forma que

\[ \Prob{\{ \, \omega \in \Omega \mid X(\omega) = x \,\}} = \Prob{X = x}. \]

De este modo, en este ejemplo tenemos que $\Prob{X = 2} = 0.375$. Del mismo modo, se utilizará la notación $(X \leq x)$ para denotar a $\{ \, \omega \in \Omega \mid X(\omega) \leq x \, \} = X^{-1}[(-\infty, x]]$. Sin embargo, ¡ten cuidado! Esta es una NOTACIÓN para facilitar la escritura de muchas de las expresiones matemáticas que involucran variables aleatorias. Aunque resulte práctica, no olvides lo que representa realmente.

Definición de variable aleatoria

De acuerdo con la motivación anterior, presentamos la definición de variable aleatoria.

Definición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Diremos que una función $X\colon\Omega \to \RR$ es una variable aleatoria si para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$.

Es decir, $X$ es una variable aleatoria si la imagen inversa bajo $X$ de cualquier evento del σ-álgebra de Borel, es un evento de $\mathscr{F}$.

En algunos contextos se usa la notación $X\colon(\Omega, \mathscr{F})\to(\RR, \mathscr{B}(\RR))$ para denotar a una variable aleatoria. Usando esta notación, se escribe explícitamente el σ-álgebra del dominio y del codominio de $X$.

Intuitivamente, una variable aleatoria es un valor numérico asociado al resultado de un experimento aleatorio. Por ejemplo, cuando hicimos el experimento de lanzar una moneda $4$ veces, el valor numérico asociado a cada uno de los posibles resultados del experimento es la cantidad de águilas que salieron en los $4$ lanzamientos.

Además, previamente acordamos que los elementos de un σ-álgebra son aquellos que se pueden medir, pues el dominio de la medida $\mathbb{P}$ es el σ-álgebra. Esencialmente, la definición de variable aleatoria pide que la función preserve la medibilidad. Es decir, que si $A$ es un subconjunto medible del codominio de $X$ (esto es, $A \in \mathscr{B}(\RR)$), entonces $X^{-1}[A]$ debe de ser un subconjunto medible del dominio de $X$; es decir, $X^{-1}[A] \in \mathscr{F}$. De este modo,

\[ \Prob{X \in A} = \Prob{X^{-1}[A]} = \Prob{\{\, \omega\in\Omega\mid X(\omega) \in A \,\}}, \]

es un valor que está bien definido, pues $X^{-1}[A] \in \mathscr{F}$ y $\mathrm{Dom}(\mathbb{P}) = \mathscr{F}$.

Una propiedad muy importante de las variables aleatorias

Hay libros introductorios a la probabilidad que prefieren no tocar con mucho detalle la definición de variable aleatoria, o darla de manera distinta. Por ejemplo, tal es el caso de A First Course In Probability de Sheldon M. Ross, o Introducción a la Probabilidad de Luis Rincón. En particular, el caso del libro del Dr. Rincón es importante, pues es el libro al que muchos estudiantes recurren al cursar esta materia. Dicho libro ofrece una definición de variable aleatoria distinta; con el siguiente teorema veremos que es equivalente a la que hemos dado aquí.

Teorema. Sean $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una función. Si $\mathcal{G} \subseteq \RR$ es un conjunto tal que $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$, entonces las siguientes proposiciones son equivalentes:

  1. $X\colon\Omega\to\RR$ es una variable aleatoria.
  2. Para todo $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$.

Demostración. $(1 \implies 2)$ Verificar que 1. implica a 2. no es complicado. Supongamos que $X$ es una variable aleatoria. Por definición, esto asegura que para cada $E \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[E] \in \mathscr{F}$.

Ahora, hay que demostrar que 2. es cierto. Sea $A \in \mathcal{G}$. Sabemos que $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$, es decir, el σ-álgebra generado por $\mathcal{G}$ es el σ-álgebra de Borel sobre $\RR$. Además, sabemos que $\sigma(\mathcal{G})$ satisface $\mathcal{G} \subseteq \sigma(\mathcal{G})$, por lo que $\mathcal{G} \subseteq \mathscr{B}(\RR)$. En consecuencia, $A \in \mathscr{B}(\RR)$, que implica $X^{-1}[A] \in \mathscr{F}$, pues $X$ es una variable aleatoria, garantizando que 2. es verdadero.

$(2 \implies 1)$ Lo interesante es demostrar que 2. implica a 1., pues 2. parece una condición más débil. Así pues, supongamos que $X$ es una función que satisface 2.; que para cada $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$. Ahora queremos demostrar que $X$ es una variable aleatoria. Es decir, queremos demostrar que para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$.

Ahora, hay algunas propiedades importantes de la imagen inversa de una función. Por tus clases de álgebra superior, sabes que para cualquier colección $\{ B_{i} \}_{i \in \mathbb{N}^{+}}$ de subconjuntos de $\RR$ se cumple que

la imagen inversa «abre» la unión: \begin{align*} X^{-1}{\left[ \bigcup_{i=1}^{\infty} B_{i} \right]} = \bigcup_{i=1}^{\infty} X^{-1}{\left[ B_{i} \right]}, \end{align*}

la imagen inversa «abre» la intersección: \begin{align*} X^{-1}{\left[ \bigcap_{i=1}^{\infty} B_{i} \right]} = \bigcap_{i=1}^{\infty} X^{-1}{\left[ B_{i} \right]}. \end{align*}

y además, para cada $B \subseteq \RR$ se cumple que $X^{-1}[\RR \setminus B] = \Omega \setminus X^{-1}[B]$. Defínase ahora $\mathcal{M}$ como sigue:

\begin{align*} \mathcal{M} = \{\, B \subseteq \RR \mid X^{-1}[B] \in \mathscr{F} \,\}. \end{align*}

Es decir, los elementos de $\mathcal{M}$ son los subconjuntos de $\RR$ tales que $X^{-1}[B] \in \mathscr{F}$. Usando las propiedades de la imagen inversa bajo $X$, es posibe demostrar que $\mathcal{M}$ es un σ-álgebra. Más aún, sabemos que para cada $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$. Por ende, $\mathcal{G} \subseteq \mathcal{M}$. Pero $\mathcal{M}$ es un σ-álgebra, y lo anterior demuestra que es un σ-álgebra que contiene a $\mathcal{G}$. En consecuencia, $\sigma(\mathcal{G}) \subseteq \mathcal{M}$.

¡Ajá! Pero $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$; por lo que $\mathscr{B}(\RR) \subseteq \mathcal{M}$. Para concluir, sea $B \in \mathscr{B}(\RR)$. Por lo anterior, se sigue que $B \in \mathcal{M}$, que por la definición de $\mathcal{M}$ significa que $X^{-1}[B] \in \mathscr{F}$, que es justamente lo que queríamos demostrar.

$\square$

Este teorema es de mucha utilidad, ya que dada una función $X\colon\Omega\to\RR$, demostrar que $X$ es una variable aleatoria es equivalente a demostrar que $X$ preserva la medibilidad sobre una familia de conjuntos que genera a $\mathscr{B}(\RR)$, una tarea mucho más sencilla que hacerlo para todos los elementos del σ-álgebra de Borel.

Definición alternativa de variable aleatoria

Previamente establecimos que $\mathscr{B}(\RR)$ es el σ-álgebra generado por varias familias de subconjuntos de $\RR$. En particular, $\mathscr{B}(\RR)$ puede generarse a partir de la familia de intervalos de la forma $(-\infty, x]$, con $x \in \RR$. Por ello, gracias al teorema que demostramos, podemos caracterizar a una variable aleatoria como sigue:

Definición (alternativa). Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Diremos que una función $X\colon\Omega\to\RR$ es una variable aleatoria si para cada $x \in \RR$ se cumple que $X^{-1}[(-\infty, x]] \in \mathscr{F}$. Esto es,

\[ \{ \, \omega \in \Omega \mid X(\omega) \leq x \, \} \in \mathscr{F}. \]

La definición anterior es la que presentan algunos libros como la definición de variable aleatoria (por ejemplo, así la encontrarás el libro del Dr. Luis Rincón, si es que decides consultarlo). No temas, ambas maneras de definir el concepto de variable aleatoria son equivalentes, todo gracias al teorema que vimos en esta entrada.

Medida de probabilidad inducida por una variable aleatoria

Dados $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una variable aleatoria, vimos que podíamos usar la medida de probabilidad $\mathbb{P}$ para medir la probabilidad de los subconjuntos de la forma $(-\infty, x]$ a través de sus imágenes inversas bajo $X$. De hecho, gracias a lo que discutimos al final de la sección pasada, resulta que esto se puede hacer para cualquier evento de $\RR$, es decir, para todos los elementos de $\mathscr{B}(\RR)$. A la medida resultante para los eventos de $\RR$ se le conoce como la medida de probabilidad inducida por $X$, y se define como sigue.

Definición. Sean $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una variable aleatoria. La medida de probabilidad inducida por $X$ es la medida de probabilidad $P_{X}: \mathscr{B}(\RR) \to \RR$ dada por

\begin{align*} P_{X}(B) &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \in B \,\}}, & \text{para cada $B \in \mathscr{B}(\RR)$. } \end{align*}

Equivalentemente, usando la notación probabilista para imágenes inversas, $P_{X}: \mathscr{B}(\RR) \to \RR$ es la función dada por

\begin{align*} P_{X}(B) &= \Prob{X \in B}, & \text{para cada $B \in \mathscr{B}(\RR)$}. \end{align*}

De este modo, si $(\Omega, \mathscr{F}, \mathbb{P})$ es un espacio de probabilidad y $X\colon\Omega\to\RR$ es una variable aleatoria, entonces $(\RR, \mathscr{B}(\RR), P_{X})$ es un espacio de probabilidad.

Ejemplos básicos de variables aleatorias

Ejemplo 1. Hay una gran cantidad de experimentos aleatorios cuyos resultados se reducen a «éxito» o «fracaso». Por ejemplo, en el lanzamiento de una moneda, el «águila» y el «sol» podrían verse como «éxito» y «fracaso», respectivamente. Comenzamos con el espacio muestral $\Omega = \{ \mathrm{«Exito», «Fracaso»} \}$. Definimos la variable aleatoria $X\colon\Omega\to\RR$ como sigue

\begin{array}{rcl} X(\mathrm{«Exito»}) & = & 1, \\ X(\mathrm{«Fracaso»}) & = & 0. \end{array}

La elección de estos dos números es un poco arbitraria, aunque obedece a la noción de que, en ciertos contextos, el $1$ es un «acierto» y el $0$ un «error». Esto pasa incluso en la lógica, en donde a veces se denota al «verdadero» como $1$ y al «falso» como $0$, sobre todo en contextos computacionales.

Como σ-álgebra tomaremos a $\mathscr{P}(\Omega)$ y como medida de probabilidad tomaremos la siguiente: sea $p \in \RR$ tal que $p \in [0,1]$. Definimos $\mathbb{P}\colon\mathscr{P}(\Omega)\to\RR$ como sigue:

\begin{array}{rcl} \Prob{\{\mathrm{«Exito»}\}} & = &p, \\ \Prob{\{\mathrm{«Fracaso»}\}} & = & 1 − p, \end{array}

\begin{array}{rcl} \Prob{\emptyset} & = & 0, \\ \Prob{\Omega} & = & p + (1 − p) = 1. \end{array}

En consecuencia, se tendrá que $\Prob{X = 1} = p$ y $\Prob{X = 0} = 1 − p$. De este modo, podemos ver que

\[ \Prob{X = x} = \begin{cases} p & \text{si $x = 1$}, \\ 1 − p & \text{si $x = 0$}, \\ 0 & \text{en otro caso}. \end{cases} \]

Esta es una variable aleatoria muy sencilla, pero muy poderosa. Más adelante, cuando ya hayamos visto más conceptos relacionados con variables aleatorias, la veremos con más detalle.

Ejemplo 2. Considera el experimento de lanzar un dado $2$ veces. El espacio muestral de este experimento es

\begin{align*} \Omega = \begin{Bmatrix} (1,1), & (1,2), & (1,3), & (1,4), & (1,5), & (1,6) \\ (2,1), & (2,2), & (2,3), & (2,4), & (2,5), & (2,6) \\ (3,1), & (3,2), & (3,3), & (3,4), & (3,5), & (3,6) \\ (4,1), & (4,2), & (4,3), & (4,4), & (4,5), & (4,6) \\ (5,1), & (5,2), & (5,3), & (5,4), & (5,5), & (5,6) \\ (6,1), & (6,2), & (6,3), & (6,4), & (6,5), & (6,6) \end{Bmatrix}, \end{align*}

tomando como σ-álgebra a $\mathscr{P}(\Omega)$ y con la medida de probabilidad clásica, $\Prob{A} = \frac{|A|}{|\Omega|}$, para cada $A \in \mathscr{P}(\Omega)$. Definimos la variable aleatoria $S\colon\Omega\to\RR$ de la siguiente manera: para cada $(\omega_{1}, \omega_{2}) \in \Omega$,

\[ S(\omega_{1}, \omega_{2}) = \omega_{1} + \omega_{2}. \]

Primero, observa que esto es algo que ya habíamos hecho antes, pero sin variables aleatorias: $S$ corresponde a la suma de los resultados de los dos lanzamientos de dado. Observa que los posibles valores que puede tomar esta variable aleatoria son los números naturales del $2$ al $12$. Por ejemplo, ¿cuál sera la probabilidad de $(S = 6)$? Para ello, veamos cuáles son los elementos de este evento.

\begin{align*} (S = 6) = \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid S(\omega_{1}, \omega_{2}) = 6 \,\} &= \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid \omega_{1} + \omega_{2} = 6 \,\} \\[0.5em] &= \{ (1,5), (2,4), (3,3), (4,2), (5,1) \}. \end{align*}

En consecuencia, tenemos que

\[ \Prob{S = 6} = \Prob{\{ (1,5), (2,4), (3,3), (4,2), (5,1) \}} = \frac{5}{36}. \]

Entonces la probabilidad de que la variable aleatoria tome el valor $6$ es de $\frac{5}{36} \approx 0.1389$.

De hecho, es posible establecer una fórmula para la probabilidad de cada resultado de este experimento. Nos quedaría como sigue:

\[ \Prob{S = s} = \begin{cases} \frac{6 – |s – 5|}{36} & \text{si $s \in \{2,3,4,5,6,7,8,9,10,11,12\}$}, \\[0.25em] 0 & \text{en otro caso}. \end{cases} \]

Observa que es necesario definir a $\Prob{S = s}$ como $0$ incluso cuando $s$ no es uno de los valores que puede tomar la variable aleatoria. Esto pasa porque los eventos de la forma $(S = s)$ están definidos para todos los $s \in \RR$, así que la probabilidad de estos eventos debe de definirse, incluso si es $0$. Por ejemplo, la probabilidad de que $(S = 7.34)$ es $0$, pues no es uno de los valores que puede tomar $S$.

Por otro lado, ¿cuál es la probabilidad de que $(S \leq 4)$? Hay que ver cuáles son los pares de lanzamientos que hacen que $S$ sea menor o igual que $4$:

\begin{align*} (S \leq 4) = \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid S(\omega_{1}, \omega_{2}) \leq 4 \,\} &= \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid \omega_{1} + \omega_{2} \leq 4 \,\} \\[0.5em] &= \{ (1,1), (1,2), (1,3), (2,1), (2,2), (3,1) \}. \end{align*}

En consecuencia se tiene que $\Prob{S \leq 4} = \frac{6}{36} = \frac{1}{6} \approx 0.1667$. Otra manera de hacerlo es sumar las probabilidades de que $S$ tome los valores menores o iguales a $4$, sobre aquellos valores que sí puede tomar. Esto es,

\begin{align*} \Prob{S \leq 4} = \sum_{k=2}^{4} \Prob{S = k} &= \Prob{S = 2} + \Prob{S = 3} + \Prob{S = 4} \\ &= \frac{1}{36} + \frac{2}{36} + \frac{3}{36} \\ &= \frac{6}{36} \\ &= \frac{1}{6} \end{align*}

Esto es algo que se cumple para aquellas variables aleatorias que pueden tomar a lo más una cantidad numerable de valores, como es el caso de $S$. Lo mismo pasa aún cuando el evento que nos interesa involucra a un valor que $S$ no puede tomar. Por ejemplo, $\Prob{S \leq 3.76}$ se puede calcular como

\[ \Prob{S \leq 3.76} = \Prob{S = 2} + \Prob{S = 3} = \frac{1}{36} + \frac{2}{36} = \frac{3}{36} = \frac{1}{12}, \]

pues los valores que puede tomar $S$ que son menores o iguales a $3.76$ son $2$ y $3$.

Las variables aleatorias de estos ejemplos son conocidas como discretas porque la cardinalidad del conjunto de valores que pueden tomar es finito. Más adelante veremos con propiedad lo que es una variable aleatoria discreta. Sin embargo, a pesar de que podemos definir muchos ejemplos de variables aleatorias con su regla de correspondencia, veremos más adelante que podemos prescindir por completo de esto. Así, lo único que importará es la probabilidad de los eventos de la forma $(X \leq x)$, sin necesidad de mencionar explícitamente a $\Omega$.

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

  1. De acuerdo con la notación probabilista adoptada en esta entrada, ¿cómo se escribe el evento $( X = 4 )$ sin usar la notación? ¿Y cómo se escribe $\{ \, \omega \in \Omega \mid X(\omega) = 3 \, \}$ utilizando la notación?
  2. De acuerdo con la notación probabilista para eventos, ¿cómo se escribe el evento $(X < x)$ explícitamente (sin usar la notación)?
  3. Verifica que $\mathcal{M}$, visto en la demostración del teorema de esta entrada, es un σ-álgebra.
  4. En el Ejemplo 2:
    1. Verifica que la fórmula que dimos para $\Prob{S = s}$ es correcta.
    2. Calcula las probabilidades de que $(S < 6)$ y $(S \leq 5)$. ¿Qué puedes observar?

Más adelante…

Más adelante veremos que las variables aleatorias se pueden dividir en distintos tipos, dependiendo del tipo de conjunto de valores que pueden tomar. Además, en la siguiente entrada veremos que existen funciones que permiten capturar la probabilidad de cualquier evento asociado a una variable aleatoria $X$. De hecho, esto incluso nos permitirá omitir casi por completo al espacio muestral $\Omega$, y lo que importará será únicamente la probabilidad de los eventos asociados a $X$.

Por otro lado, en el contexto más general de la teoría de la medida, el concepto que definimos como variable aleatoria es conocido como función medible.

Entradas relacionadas