Introducción
Hemos conocido en esta unidad las transformaciones lineales y que a partir de ellas podemos asociarles una matriz única. En la sección anterior comenzamos con las primeras operaciones entre matrices: el producto de matrices y su estrecha relación con la composición de matrices. En esta unidad veremos las matrices más representativas y sus funciones lineales a las cuales están asociadas.
Matriz identidad
No es una familia de matrices, pero es el primer tipo de matriz que debemos mencionar. La matriz identidad está asociada a la función identidad y su tamaño es de $n\times n$, es decir el número de filas es el mismo que el de columnas. Se denota por $I$ pero como se tiene una matriz identidad para cada dimensión, se puede escribir como $I_n$.
La matriz identidad se caracteriza porque todos sus elementos son ceros ($0$) excepto aquellos elementos que se encuentran en la diagonal principal, que son unos ($1$).
Ejemplo. Para la función identidad $f: \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, su matriz identidad asociada es
\[ I_2 = I_{2 \times 2} = \left(\begin{array}{cc}
1&0\\
0&1
\end{array} \right), \]
y para la función identidad $f: \mathbb{R}^n \longrightarrow \mathbb{R}^n$, su matriz identidad asociada es
\[ I_n = I_{n \times n} = \left(\begin{array}{cccc}
1&0&\cdots&0\\
0&1&\cdots&0\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\cdots&1
\end{array} \right). \]
De hecho el producto de cualquier matriz por a matriz identidad no tiene ningún efecto, ya que siempre se cumple que $AI = A$ e $IA = A$.
Homotecias
Las homotecias son funciones de cambios de escala, porque conservan los ángulos pero no las distancias entre cualquier par de puntos. Sin embargo, todas las distancias se incrementan o disminuyen en una misma razón $k \in \mathbb{R}$, con $k \neq 0$, para una función $f: \mathbb{R}^n \longrightarrow \mathbb{R}^n$ definida por $f(x) = kx$, la cual es lineal.
La matriz asociada a estas funciones es $kI$, es decir la matriz que sólo tiene elementos $k$ en la diagonal principal y ceros ($0$) fuera de dicha diagonal. Cuando $k>1$ aumentan las distancias (dilataciones), cuando $k<1$ disminuyen (contraen) y en caso de que $k=1$, las distancias se conservan.
Ejemplo. Para el caso de una función lineal $f: \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, la matriz de homotecia de $2\times 2$ asociada es de la forma
\[ I_n = I_{n \times n} = \left(\begin{array}{cc}
k&0\\
0&k
\end{array} \right), \]
Ejemplo. Dada la función lineal definida por
\[ f \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{c}
\frac{x}{4}\\
\frac{y}{4}
\end{array} \right), \]
cuya matriz asociada es
\[ \left(\begin{array}{cc}
\frac{1}{4}&0\\
0&\frac{1}{4}
\end{array} \right), \]
ya que
\[ f \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{cc}
\frac{1}{4}&0\\
0&\frac{1}{4}
\end{array} \right) \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{c}
\frac{x}{4}\\
\frac{y}{4}
\end{array} \right).\]
Vemos que la función corresponde a una homotecia que reduce las distancias entre cualquier par de puntos en una razón de $\frac{1}{4}$.
Rotaciones
Recordemos que en las rotaciones, todo el plano gira un ángulo $\alpha$ alrededor de un punto fijo (el origen del sistema coordenado) pero permanecen invariantes el tamaño y forma de las figuras.
Las columnas de la matriz asociada a las rotaciones en $\mathbb{R}^2$ con centro en el origen mediante un ángulo $\alpha$ son:
\[ f(e_1) = \left(\begin{array}{c}
cos\, \alpha\\
sen\, \alpha
\end{array} \right), \hspace{0.5cm} y \hspace{0.5cm} f(e_2)= \left(\begin{array}{c}
-sen\, \alpha\\
cos\, \alpha
\end{array} \right). \]
En consecuencia las rotaciones mandan al vector canónico $e_1$ en un vector unitario $u$ y al vector canónico $e_2$ en su vector ortogonal $u^{\perp}.$
Por tanto, para una función lineal $f: \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, su matriz de rotación asociada correspondiente es
\[ R_{\alpha} = \left(\begin{array}{cc}
cos\, \alpha & -sen\, \alpha\\
sen\, \alpha & cos\, \alpha
\end{array} \right). \]
Ejemplo. Si $\alpha = 45°$ y queremos calcular la rotación de $45°$del vector $\vec{x}$ entonces la matriz en este caso será:
\begin{align*}
R_{45°}(\vec{x}) &= \left(\begin{array}{cc}
cos\, 45°& -sen\, 45°\\
sen\, 45°& cos\, 45°
\end{array} \right) \vec{x}\\
&= \left(\begin{array}{cc}
\frac{\sqrt{2}}{2}& -\frac{\sqrt{2}}{2}\\
\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}
\end{array} \right) \vec{x}.
\end{align*}
Un hecho importante es que una vez que hubo una rotación de ángulo $\alpha$ y volvemos a aplicar una rotación pero de ángulo $-\alpha$, regresaremos a la matriz identidad. Es decir que con la ayuda de las igualdades
\[ cos\, (-\alpha) = cos\, \alpha \hspace{0.5cm} y \hspace{0.5cm} sen\, (-\alpha) = – sen \, \alpha,\]
se cumple que $R_{-\alpha}\, R_{\alpha} = I$. Este resultado lo dejaremos como ejercicio en la sección Tarea moral.
Ahora bien, si rotamos un ángulo $\beta$ y posteriormente un ángulo $\alpha$, rotamos entonces en total un ángulo $\alpha + \beta$, entonces se cumple que $R_{\alpha}\, R_{\beta} = R_{\alpha + \beta}$, pues
\begin{align*}
R_{\alpha}\, R_{\beta} &= \left(\begin{array}{cc}
cos\, \alpha& -sen\, \alpha\\
sen\, \alpha& cos\, \alpha
\end{array} \right) \left(\begin{array}{cc}
cos\, \beta& -sen\, \beta\\
sen\, \beta& cos\, \beta
\end{array} \right) \\
&= \left(\begin{array}{cc}
cos\, \alpha \, cos \, \beta \,- \, sen\, \alpha\, sen\, \beta & -cos\, \alpha \, sen \, \beta \,- \, sen\, \alpha\, cos\, \beta\\
sen\, \alpha \, cos \, \beta \,+ \, cos\, \alpha\, sen\, \beta & -sen\, \alpha \, sen \, \beta \, + \, cos\, \alpha\, cos\, \beta
\end{array} \right) \\
&= \left(\begin{array}{cc}
cos(\alpha + \beta)& -sen(\alpha + \beta)\\
sen(\alpha + \beta)& cos(\alpha + \beta)
\end{array} \right) = R_{\alpha + \beta},
\end{align*}
obteniendo las fórmulas trigonométricas para el coseno y el seno de la suma de ángulos como consecuencia de la composición de funciones y la multiplicación de matrices.
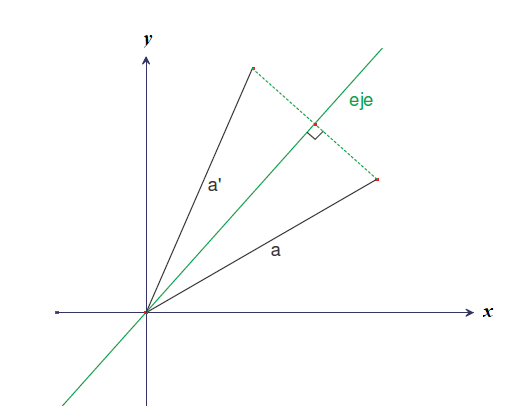
Reflexiones
Para ver el significado geométrico que una reflexión ejerce sobre un vector, consideremos las funciones lineales:
- Sea $f : \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, tal que $f \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{c}
-x\\
y
\end{array} \right) $ se llama reflexión con respecto al eje $y$. - Sea $f : \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, tal que $f \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{c}
x\\
-y
\end{array} \right) $ se llama reflexión con respecto al eje $x$. - Sea $f : \mathbb{R}^2 \longrightarrow \mathbb{R}^2$, tal que $f \left(\begin{array}{c}
x\\
y
\end{array} \right) = \left(\begin{array}{c}
y\\
x
\end{array} \right) $ se llama reflexión con respecto a la recta $y=x$.
La representación matricial de cada caso es
\[ R_y = \left(\begin{array}{cc}
-1&0\\
0&1
\end{array} \right), \hspace{0.5cm} R_x = \left(\begin{array}{cc}
1&0\\
0&-1
\end{array} \right), \hspace{0.5cm} R_{y=x} = \left(\begin{array}{cc}
0&1\\
1&0
\end{array} \right), \]
respectivamente. De forma más general, las reflexiones deben parametrizarse por la mitad del ángulo de la imagen de $e_1$, quien es el ángulo de la recta respecto a la cual se hace la reflexión. Con ello, la reflexión en la recta con ángulo $\theta$ manda a $e_1$ en el vector unitario de ángulo $2\theta$, y su matriz asociada es:
\[ E_{\theta} = \left(\begin{array}{cc}
cos\, 2\theta & sen\, 2\theta \\\
sen\, 2\theta & -cos\, 2\theta
\end{array} \right) \]
Dejaremos como ejercicio moral ver que se cumplen $E_{\theta} E_{\theta} = I$ y que la composición de reflexiones es $E_{\alpha} E_{\beta}= R_{2(\alpha – \beta).}$
Matrices ortogonales
Una matriz ortogonal debe cumplir ser cuadrada y su función lineal asociada debe ser ortogonal (es decir, que preserva el producto interior). Entonces, para que se cumplan dichas condiciones, recurrimos a la siguiente definición:
Definición. Una matriz A de $n\times n$ es ortogonal (la matriz de una transformación ortogonal) si y sólo si $A \cdot A^T = I$.
Ejemplo. Para la matriz de reflexión con respecto a la recta $x=y$
\[
A = \left(\begin{array}{cc}
0&1\\
1&0
\end{array} \right),
\]
el producto de A con su transpuesta $A^T$ es
\[
A \cdot A^T = \left(\begin{array}{cc}
0&1\\
1&0
\end{array} \right) \left(\begin{array}{cc}
0&1\\
1&0
\end{array} \right) = \left(\begin{array}{cc}
1&0\\
0&1
\end{array} \right) = I
\]
Ejemplo. Para la matriz de rotación
\[ B = \left(\begin{array}{cc}
cos\, \alpha & sen\, \alpha\\
-sen\, \alpha & cos\, \alpha
\end{array} \right), \]
el producto de B con su transpuesta $B^T$ es
\[
B \cdot B^T = \left(\begin{array}{cc}
cos\, \alpha & -sen\, \alpha\\
sen\, \alpha & cos\, \alpha
\end{array} \right) \left(\begin{array}{cc}
cos\, \alpha & sen\, \alpha\\
-sen\, \alpha & cos\, \alpha
\end{array} \right) = \left(\begin{array}{cc}
1&0\\
0&1
\end{array} \right) = I.
\]
De hecho las matrices ortogonales de $2 \times 2$ son: las rotaciones y las reflexiones.
Tarea moral
- ¿Las siguientes matrices son matrices identidad?
\[ A = \left(\begin{array}{cc}
1&1\\
0&3
\end{array} \right), \hspace{0.5cm} B = \left(\begin{array}{cc}
1&0\\
0&1\\
0&0
\end{array} \right), \hspace{0.5cm} C = \left(\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&1
\end{array} \right), \]
2. Demostrar que las homotecias tienen la propiedad de conmutar con cualquier otra matriz, es decir, $A(kI) = (kI) A$, donde $k$ es una constante real, $I$ es la matriz identidad y $A$ una matriz de $n\times n$.
3. Demostrar que la rotación de un ángulo $-\theta$ nos regresa a la unidad, es decir, probar que se cumple $R_{-\theta}R_{\theta}= I$
4. En la sección de reflexiones de esta entrada definimos a la matriz $E_{\theta}$. Demostrar que se cumple $E_{\theta} E_{\theta} = I$ y que la composición de reflexiones es $E_{\alpha}E_{\beta}= R_{2(\alpha – \beta).}$
Más adelante
En la siguiente entrada vamos a conocer al grupo de matrices invertibles de $n\times n$, el grupo general lineal de orden $n$; a las cuales pertenecen las matrices ortogonales. Además veremos la forma más fácil de saber si una matriz de $2\times 2$ es invertible, mediante el determinante y su relación con los sistemas de dos ecuaciones lineales con dos incógnitas.
Enlaces relacionados
- Página principal del curso:
- Entrada anterior del curso:
- Siguiente entrada del curso: