Introducción.
En la entrada pasada vimos dos ejemplos importantes de conjuntos medibles y algunas resultados básicos de operaciones con conjuntos. En esta entrada veremos algunos resultados similares, pero ahora con una cantidad numerable de elementos. Estableceremos también la aditividad numerable de la medida de Lebesgue y un par de resultados relacionados.
Proposición. Si $A_1,A_2,\dots$ es una familia numerable de conjuntos medibles ajenos dos a dos, entonces $A=\bigcup_{k=1}^{\infty} A_k$ es medible.
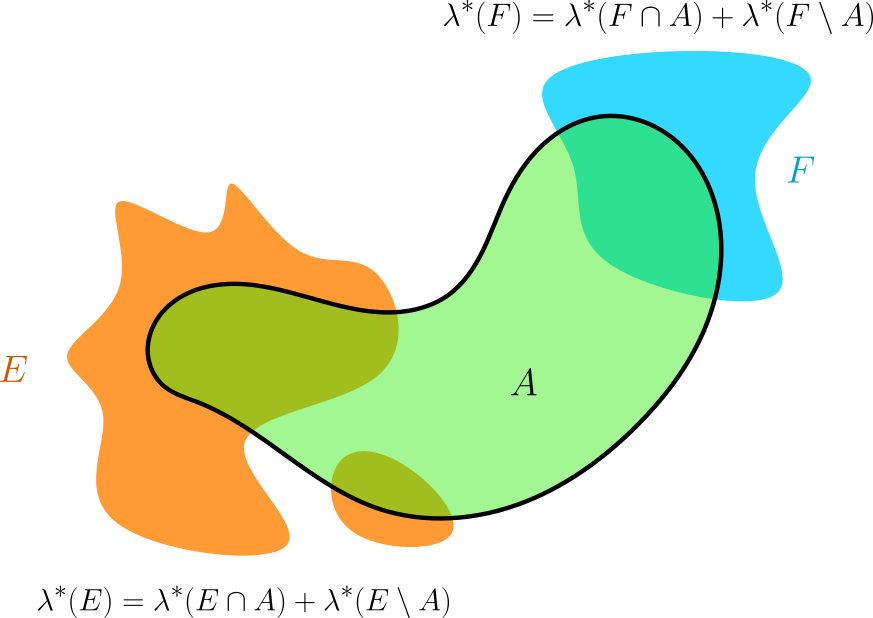
Demostración. Definamos $U_0=\emptyset$ y para cada $m=1,2,\dots$, $U_m=\bigcup_{k=1}^{m}A_k$. Por la cerradura de la clase de conjuntos medibles bajo uniones finitas, sabemos que $U_m$ es medible para todo $m\in \mathbb{N}$. Como $A_m$ es medible, para cualquier $E \subseteq \mathbb{R}^n$:
\begin{align*} \lambda^*(E\cap U_m) &= \lambda^*(E\cap U_m \cap A_m)+\lambda^*(E\cap U_m \cap A_m^c) \\ &= \lambda^*(E\cap A_m) + \lambda(E\cap U_{m-1}). \end{align*} Luego, por inducción se sigue que: $$\lambda^*(E\cap U_m)=\sum_{k=1}^{m} \lambda^*(E\cap A_k).$$ Como $U_m$ es medible: \begin{align*}
\lambda^*(E) &= \lambda^*(E\cap U_m) + \lambda^*(E\cap U_m^c) \\ &\geq \sum_{k=1}^{m} \lambda^*(E\cap A_k) + \lambda^*(E\cap A^c). \end{align*} La última desigualdad se cumple pues $U_m\subseteq A$. Haciendo tender $m\to \infty$ en la expresión anterior tenemos:
\begin{align*} \lambda^*(E) &\geq \sum_{k=1}^{\infty} \lambda^*(E\cap A_k)+\lambda^*(E\cap A^c) \\ &\geq \lambda^*\left(\bigcup_{k=1}^{\infty}(E\cap A_k)\right)+\lambda^*(E\cap A^c) \\ &= \lambda^*(E\cap A)+ \lambda^*(E\cap A^c) \\ &\geq \lambda^*(E). \end{align*} (La segunda y última desigualdad se tienen por subaditividad). Luego, las desigualdades anteriores son de hecho igualdades. En particular $$ \lambda^*(E)=\lambda^*(E\cap A)+ \lambda^*(E\cap A^c).$$ Como esto es cierto para cualquier $E\subseteq \mathbb{R}^n$, se sigue que $A$ es medible.
$\square$
Observación. Al tomar $E=A$ en la última cadena de (des)igualdades en la proposición anterior podemos deducir:
$$ \lambda(A)=\lambda^*(A)=\sum_{k=1}^{\infty} \lambda^*(A_k)=\sum_{k=1}^{\infty} \lambda(A_k). $$
Esto es precisamente la aditividad numerable. Lo enunciaremos como una proposición.
Proposición (Aditividad numerable o Sigma-aditividad). Si $A_1, A_2,\dots$ es una familia numerable de conjuntos medibles ajenos dos a dos, entonces:
$$ \lambda(A)=\sum_{k=1}^{\infty} \lambda(A_k) .$$
$\square$
Proposición. Si $A_1,A_2\dots$ es una familia de conjuntos medibles (no necesariamente ajenos) entonces $A=\bigcup_{k=1}^{\infty} A_k$ es medible.
Demostración. La idea es reducirlo al caso de conjuntos ajenos con una elección adecuada de conjuntos. A ésta técnica se le conoce comúnmente como ajenización.
Definamos $B_1=A_1$ y $B_m=A_m\setminus (\bigcup_{k=1}^{m-1} A_k)$ para $m\geq 2$. Cada $B_m$ es medible (por propiedades de los conjuntos medibles). Además, es fácil verificar usando inducción que $B_1,B_2\dots $ es una familia de conjuntos ajenos dos a dos y que para cada $m=1,2,\dots$, $$\bigcup_{k=1}^{m}A_k=\bigcup_{k=1}^{m}B_k.$$ Así pues $A=\bigcup_{k=1}^{\infty}A_k=\bigcup_{k=1}^{\infty}B_k$ es medible por la proposición anterior.
$\square$
Usando el resultado anterior y las leyes de De Morgan se sigue fácilmente:
Proposición. Si $A_1,A_2\dots$ es una familia de conjuntos medibles, entonces $A=\bigcap_{k=1}^{\infty} A_k$ es medible.
$\square$
La demostración se queda como tarea moral.
Proposición (Monotonía de la medida de Lebesgue).
- Si $A_k$ es una sucesión creciente de conjuntos medibles, i.e. $A_1\subseteq A_2 \subseteq \dots$, entonces $$ \lambda\left(\bigcup_{k=1}^{\infty}A_k\right) = \lim_{k\to \infty} \lambda(A_k).$$
- Si $A_k$ es una sucesión decreciente de conjuntos medibles, i.e. $A_1\supseteq A_2\supseteq \dots$ y $\lambda(A_1)\leq \infty$, entonces $$ \lambda\left(\bigcap_{k=1}^{\infty}A_k\right) = \lim_{k\to \infty} \lambda(A_k).$$
Demostración. 1. Por la cerradura de conjuntos medibles bajo uniones numerables, claramente el conjunto en cuestión es medible así que tiene sentido hablar de su medida de Lebesgue. Si $\lambda(A_N)=\infty$ para algún $N$, entonces la igualdad se da de manera obvia pues necesariamente $\lambda(A_k)=\infty$ para $k\geq N$. Así que podemos suponer sin pérdida de generalidad que $\lambda(A_k)<\infty$ para todo $k$.
Nuevamente podemos ajenizar: Definamos $U_1=A_1$, $U_m=A_m\setminus (\bigcup_{k=1}^{m-1}A_k)=A_m\setminus A_{m-1}$ (en la última igualdad usamos que la sucesión es creciente). De nuevo se satisface que $U_1,U_2\dots$ es una colección de conjuntos medibles ajenos con $\bigcup_{k=1}^{m}U_k=\bigcup_{k=1}^{m}A_k$. Se sigue entonces por la aditividad numerable: $$\lambda\left(\bigcup_{k=1}^{\infty}A_k\right)=\lambda\left( \bigcup_{k=1}^{\infty}U_k\right)=\sum_{k=1}^{\infty} \lambda (U_k)=\lim_{m\to \infty} \sum_{k=1}^{m} \lambda (U_k).$$
Ahora, como $U_m=A_m\setminus A_{m-1}$ para $m\geq 2$ y los $A_m$ son de medida finita, tenemos que $\lambda(U_m)=\lambda(A_m)-\lambda(A_{m-1})$, de modo que la suma $\sum_{k=1}^{m} \lambda (U_k)$ es simplemente $\lambda(A_m)$. Sustituyendo en la expresión anterior:
$$\lambda(\bigcup_{k=1}^{\infty}A_k)=\lim_{m\to \infty} \sum_{k=1}^{m} \lambda (U_k)=\lim_{m\to \infty} \lambda(A_m).$$ Como queríamos probar.
2. Similarmente al caso anterior, el conjunto $ \bigcap_{k=1}^{\infty}A_k $ es medible. Definamos $V_m=A_1\setminus A_m$, de modo que $V_1,V_2,\dots$ es una sucesión creciente de conjuntos medibles, donde cada conjunto está contenido en $A_1$. Por el inciso anterior se sigue que: $$\lambda\left(\bigcup_{k=1}^{\infty}V_k\right)=\lim_{k\to \infty} \lambda(V_k)=\lim_{k\to \infty} [\lambda(A_1)-\lambda(A_k)]=\lambda(A_1)-\lim_{k\to \infty} \lambda(A_k).$$
De las definiciones se sigue fácilmente que $\bigcup_{k=1}^{\infty}V_k=A_1\setminus (\bigcap_{k=1}^{\infty}A_k)$, de donde $$\lambda\left(\bigcup_{k=1}^{\infty}V_k \right)=\lambda(A_1)-\lambda\left(\bigcap_{k=1}^{\infty}A_k \right).$$ Combinando las dos igualdades anteriores concluimos $$ \lambda\left(\bigcap_{k=1}^{\infty}A_k\right) = \lim_{n\to \infty} \lambda(A_k).$$
$\square$
Observación. El límite en el inciso 1 es un límite creciente, que denotaremos como $\lambda(A_k)\uparrow \lambda(\bigcup_{k=1}^{\infty}A_k)$, mientras que en el inciso 2 es un límite decreciente que denotaremos como $\lambda(A_k)\downarrow \lambda(\bigcap_{k=1}^{\infty}A_k)$. En general la hipótesis de que $A_1$ (o al menos algún $A_m$) sea de medida finita no se puede relajar, como se muestra en el siguiente ejemplo.
Ejemplo. Considera la sucesión decreciente de conjuntos $A_m=[m,\infty)$. Cada uno de estos es medible al ser una unión numerable de intervalos cerrados, sin embargo, $\lambda(A_m)=\infty$ para todo $m$, mientras que $\bigcap_{k=1}^{\infty} A_k=\emptyset$, así que en este caso: $$\lim_{m\to \infty} \lambda(A_m)=\infty \neq 0 =\lambda(\emptyset)=\lambda(\bigcap_{k=1}^{\infty} A_k).$$
$\triangle$
Más adelante…
Continuaremos con nuestro estudio de los conjuntos medibles. Veremos algunas definiciones alternas de conjunto medible y cómo es que podemos «aproximar» estos conjuntos por otros más sencillos.
Tarea moral
- Demuestra que Si $A_1,A_2\dots$ es una familia de conjuntos medibles, entonces $A=\bigcap_{k=1}^{\infty} A_k$ es medible.
- Supón que los conjuntos $A_1,A_2,\dots, A_m$ son medibles y «casi disjuntos», en el sentido que $\lambda(A_i\cap A_j)=0$ $\forall i\neq j$. Prueba que $$\lambda\left( \bigcup_{k=1}^{m}A_k \right)=\sum_{k=1}^{m}\lambda(A_k).$$
- Prueba que si $A_1,A_2,\dots, A_m$ son medibles y satisfacen $$\lambda\left( \bigcup_{k=1}^{m}A_k \right)=\sum_{k=1}^{m}\lambda(A_k).$$ Entonces los conjuntos son «casi disjuntos».
- (Lema de Borel-Cantelli). Supongamos que $A_1,A_2\dots$ es una sucesión de conjuntos medibles tales que $$\sum_
{k=1}^{\infty}\lambda(A_k)<\infty.$$ Definimos $$\limsup_{k\to \infty} A_k = \bigcap_{j=1}^{\infty}\bigcup_{l=j}^{\infty}A_l.$$ (Observa que $\limsup_{k\to \infty} A_k$ es el conjunto de $x$ tales que $x\in A_k$ para una cantidad infinita de $k$). Prueba que $$\lambda(\limsup_{k\to \infty} A_k)=0.$$ - Sea $B\subseteq \mathbb{R}^n$ un conjunto medible con $\lambda(B)<\infty$. Sean $A_1,A_2\dots \subseteq B$ una sucesión de subconjuntos medibles de $B$ tales que existe $\varepsilon>0$ con $\lambda(A_k)\geq\varepsilon$ para todo $k\in \mathbb{N}$. Demuestra que existe un punto que pertenece a una cantidad infinita de los conjuntos $A_k$.