Encontrar los valores extremos de $f (x, y) = \Big( x \, – \, \dfrac{1}{2} \Big)^2 + \Big( y \, – \, \dfrac{1}{2} \Big)^2$ sujeta a la restricción $(x, y) \in \mathcal{K}$ donde

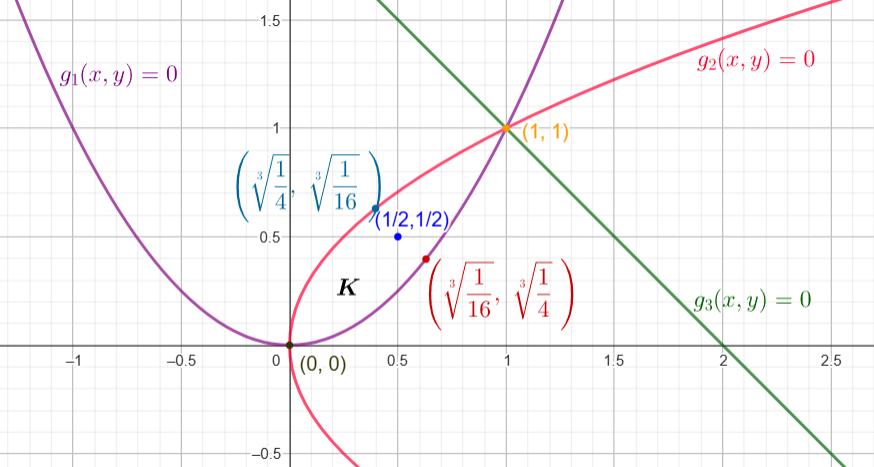
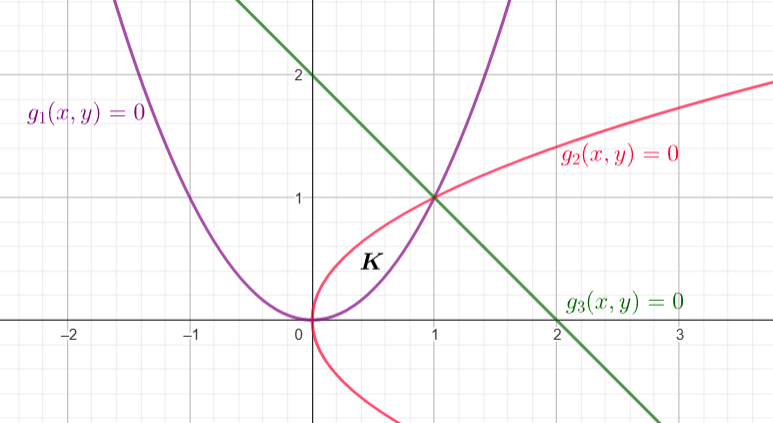
$\mathcal{K} = \Big\{ (x, y) \in \mathbb{R}^2 \, \big| \, g_1 (x, y) = y \, – \, x^2 = 0 , g_2 (x, y) = x \, – \, y^2 = 0, g_3 (x, y) = 2 \, – \, x \, – \, y = 0 \Big\}$

Calculamos las siguientes derivadas

$\nabla g_1 (x, y) = ( \, – \, 2x, 1) \neq \vec{0}$

$\nabla g_2 (x, y) = ( 1, \, – \, 2y ) \neq \vec{0}$

$\nabla g_3 (x, y) = ( \, – \, 1, \, – \, 1) \neq \vec{0}$

Buscando las intersecciones de $g_1 \cap g_2$, $g_2 \cap g_3$ y $g_1 \cap g_3$ se obtienen los posibles vértices que son los siguientes puntos:

$( 1, 1)$, $(\, – \, 2, 4)$, $(0, 0)$, $(1, 1)$, $(1, 1)$ y $(\, – \, 4, 2).$

Ahora tenemos que checar que puntos cumplen con la restricción:

$ y \, – \, x^2 \geq 0$, $ x \, – \, y^2 \geq 0$ y $ 2 \, – \, x \, – \, y \geq 0$

Por ejemplo: ¿ el punto $( \, – \, 2, 4)$ cumple con la primera desigualdad?

$ y \, – \, x^2 = 4 \, – \, (4)^2 = 4 \, – \, 16 = \, – \, 12 \ngeq 0$, por lo tanto no cumple con la primera desigualdad, luego no es vértice de $\mathcal{K}.$

Análogamente con los demás posibles vértices.

Luego, los puntos $(0, 0)$ y $(1, 1)$ son los vértices de $\mathcal{K}.$

Paso (1):

Encontrar los vértices: los puntos $(0, 0)$ y $(1, 1)$ son los vértices.

En $ f (0, 0) = f (1,1) = \frac{1}{2}$ se tiene máximo global.

Paso (2):

Aplicar multiplicadores de Lagrange en cada lado.

Lado $\mathcal{C}_1$ restricción $g_1 (x, y) = 0$

$y \, – \, x^2 = 0$ . . . (a)

$\nabla f = \lambda \nabla g$

$\begin{pmatrix} \dfrac{\partial f}{\partial x} \\ \\ \dfrac{\partial f}{\partial y} \end{pmatrix} = \lambda \begin{pmatrix} \dfrac{\partial g}{\partial x} \\ \\ \dfrac{\partial g}{\partial y} \end{pmatrix} \; \iff \; \begin{pmatrix} 2x \, – \, 1 \\ \\ 2y \, – \, 1 \end{pmatrix} = \lambda \begin{pmatrix} \, – \, 2x \\ \\ 1 \end{pmatrix}$

por lo que se tienen las siguientes ecuaciones:

$ 2x \, – \, 1 = \, – \, 2 \lambda x$ . . . (b)

$ 2y \, – \, 1 = \lambda $ . . . (c)

Luego, las ecuaciones (a), (b) y (c) forman un sistema de 3×3. Resolviendo el sistema se obtiene que:

$ x = \sqrt[3]{\dfrac{1}{4}}$ , $ y = \sqrt[3]{\dfrac{1}{16}}$

Por lo que en el lado $\mathcal{C}_1$ el punto es el $\Bigg( \sqrt[3]{\dfrac{1}{4}} , \sqrt[3]{\dfrac{1}{16}} \Bigg)$

Análogamente, en el lado $\mathcal{C}_2$ el punto es $\Bigg( \sqrt[3]{\dfrac{1}{16}} , \sqrt[3]{\dfrac{1}{4}} \Bigg)$

Paso (3):

Encontrar los puntos críticos de $ f$ sin restricciones.

$\nabla f = \vec{0}$

$\iff \; 2 \Big( x \, – \, \dfrac{1}{2}\Big) = 0 \; \rightarrow \; x = \dfrac{1}{2}$

$\iff \; 2 \Big( y \, – \, \dfrac{1}{2}\Big) = 0 \; \rightarrow \; y = \dfrac{1}{2}$

Por lo que el mínimo local es $ f (x , y) = f \Bigg( \dfrac{1}{2} , \dfrac{1}{2} \Bigg) = 0$