Recordemos que para funciones $f : \mathbb{R} \rightarrow \mathbb{R}$, si $f$ alcanza un valor máximo, o un valor mínimo, en $ x_0 $ y $f $ es derivable en $x_0$ entonces, $f’ (x_0) = 0.$ Ahora tendremos:
Si $f : \mathbb{R}^n \rightarrow \mathbb{R}$ alcanza un valor máximo, o mínimo, en $\vec{x_0}$ y $f$ es diferenciable entonces $$ \nabla f (\vec{x_0}) = \Big( \dfrac{\partial f}{\partial x_1} (x_0), \dfrac{\partial f}{\partial x_2} (x_0), \dots , \dfrac{\partial f}{\partial x_n} (x_0)\Big) = \vec{0}$$
Equivalentemente, la diferencial de $f$ en $\vec{x_0}$ es $d f (\vec{x_0}) : \mathbb{R}^n \rightarrow \mathbb{R}$ es la función constante CERO.
Geométricamente: Si $ f : \mathbb{R}^2 \rightarrow \mathbb{R} $, entonces el plano tangente a la superficie $ z = f (x, y) $ en el punto $(x_0, y_0, z_0)$ donde se alcanza el valor extremo es horizontal.
Tenemos las siguientes generalizaciones:
Si $f : \mathbb{R}^2 \rightarrow \mathbb{R} $ y $\vec{x_0} \in \mathbb{R}^n$ es un punto crítico de $f$ si $\nabla f (\vec{x_0}) = \vec{0}$, es decir, si $ d f_{\vec{x_0}} \equiv 0.$
(*) $y_1 \in \mathbb{R}$ es un valor regular si $ f^{-1} (y_1) $ es un conjunto que no contiene ningún punto crítico.
(*) $f : \mathbb{R} \rightarrow \mathbb{R} $ curva parametrizada es regular si $f’ (t) \neq \vec{0}$ para toda $t$, $t_0$ es un punto crítico si $f’ (t_0) = \vec{0}.$
(*) $f : \mathbb{R}^n \rightarrow \mathbb{R}^m $ y $\vec{x_0} \in \mathbb{R}^n$ es un punto crítico si $d f_{\vec{x_0}} : \mathbb{R}^n \rightarrow \mathbb{R}^m$ tiene el rango igual al máximo posible.
${}$
Derivadas parciales iteradas (mixtas)
Sea $f : U \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$ con $U$ abierto, y $(x_0, y_0) \in U.$
Supongamos que existen
$\dfrac{ \partial f}{ \partial x} : U \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$
$\dfrac{ \partial f}{ \partial y} : U \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$
Conceptualmente
$\dfrac{ \partial }{ \partial y } \dfrac{ \partial f}{ \partial x}$ y $ \dfrac{ \partial }{ \partial x } \dfrac{ \partial f}{ \partial y}$ podrían ser diferentes.
Veamos un ejemplo:
Consideremos la función $ f : \mathbb{R}^2 \rightarrow \mathbb{R}$
$\begin{equation*} f (x, y) = \begin{cases} \dfrac{xy ( x^2 \, – \, y^2) }{x^2 + y^2} & \text{ si } (x, y) \neq (0, 0) \\ {} \\ 0 & \text{ si } (x, y) = (0, 0) \end{cases} \end{equation*}$
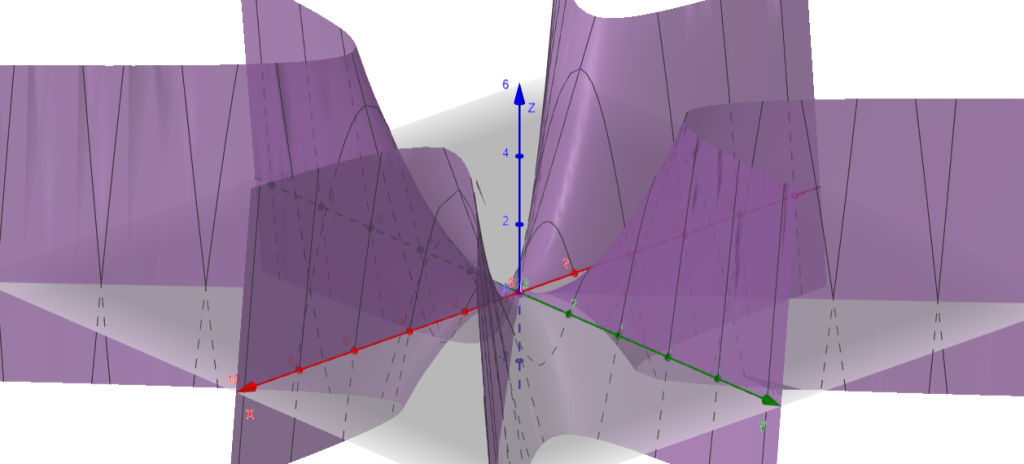
Afirmación: existen las derivadas parciales $\dfrac{ \partial }{ \partial y } \dfrac{ \partial f}{ \partial x} \Biggm|_{(0, 0)} $, $\dfrac{ \partial }{ \partial x } \dfrac{ \partial f}{ \partial y} \Biggm|_{(0, 0)} $, y son diferentes.
Veamos como calcular el siguiente límite.
Tenemos que:
$\dfrac{ \partial }{ \partial y } \dfrac{ \partial f}{ \partial x} \Biggm|_{(0, 0)} = \lim\limits_{k \to 0} \dfrac{ \dfrac{ \partial f}{ \partial x} (0, k) \, – \, \dfrac{ \partial f}{ \partial x} (0, 0) }{k} $ , llamaremos a esta expresión (1).
Para calcular esto necesitamos calcular primero las siguientes derivadas parciales:
$\dfrac{ \partial f}{ \partial x} (0, 0) = \lim\limits_{h \to 0} \dfrac{f (h, 0) \, – \, f (0, 0)}{h} = 0$
También necesitamos calcular
$\begin{align*} \dfrac{ \partial f}{ \partial x} (0, k) &= \lim\limits_{h \to 0} \dfrac{f (h, k) \, – \, f (0, k)}{h} \\ &= \lim\limits_{h \to 0} \dfrac{\dfrac{\cancel{h}k (h^2 \, – \, k^2)}{h^2 + k^2} \, – \, 0}{\cancel{h}} \\ &= \lim\limits_{h \to 0} \dfrac{k (h^2 \, – \, k^2)}{h^2 + k^2} \\ &= – \, \dfrac{k^3}{k^2} \\ \\ \dfrac{\partial f}{\partial x} (0, k) &= – \, k \end{align*}$
Entonces la expresión (1) queda de la siguiente manera:
$\dfrac{ \partial }{ \partial y } \dfrac{ \partial f}{ \partial x} \Biggm|_{(0, 0)} = \lim\limits_{k \to 0} \dfrac{ – \, k \, – \, 0 }{k} = \lim\limits_{k \to 0} – \, 1 = – \, 1$
Análogamente, para calcular
$\dfrac{ \partial }{ \partial x } \dfrac{ \partial f}{ \partial y} \Biggm|_{(0, 0)} = \lim\limits_{h \to 0} \dfrac{ \dfrac{ \partial f}{ \partial y} (h, 0) \, – \, \dfrac{ \partial f}{ \partial y} (0, 0) }{h} $ , llamaremos a esta expresión (2).
Calculemos primero las siguientes derivadas parciales:
$\dfrac{ \partial f}{ \partial y} (0, 0) = \lim\limits_{k \to 0} \dfrac{f (0, k) \, – \, f (0, 0)}{k} = \lim\limits_{k \to 0} \dfrac{0}{k} = 0$
y también
$\begin{align*} \dfrac{ \partial f}{ \partial y} (h, 0) &= \lim\limits_{k \to 0} \dfrac{f (h, k) \, – \, f (h, 0)}{k} \\ &= \lim\limits_{k \to 0} \dfrac{\dfrac{h \cancel{k} (h^2 \, – \, k^2)}{h^2 + k^2} \, – \, 0}{\cancel{k}} \\ &= \lim\limits_{k \to 0} \dfrac{h (h^2 \, – \, k^2)}{h^2 + k^2} \\ &= \dfrac{h^3}{h^2} \\ \\ \dfrac{\partial f}{\partial y} (h, 0) &= h \end{align*}$
Entonces la expresión (2) queda de la siguiente manera:
$\dfrac{ \partial }{ \partial x } \dfrac{ \partial f}{ \partial y} \Biggm|_{(0, 0)} = \lim\limits_{h \to 0} \dfrac{ h \, – \, 0 }{h} = \lim\limits_{k \to 0} 1 = 1$
De lo anterior, podemos observar que las derivadas parciales existen y son diferentes.
${}$
Entonces, quizás te preguntes, ¿existen funciones tales que sus derivadas parciales iteradas (o mixtas) sean iguales?; ¿cuáles son las funciones para las cuales sus derivadas parciales iteradas (o mixtas) son iguales?
Para responder a estas preguntas tenemos el siguiente teorema.
${}$
Teorema (de Fubini)
Si $ f $ es de clase $\mathcal{C}^2$ (es decir, que las segundas derivadas existen y son continuas) entonces las derivadas parciales iteradas ( o mixtas) son iguales.
Sea $ f : U \subset \mathbb{R}^2 \rightarrow \mathbb{R}$ donde $U$ es abierto, y $(x_0, y_0) \in U$ entonces $$ \dfrac{\partial^2 f }{\partial y \partial x} (x_0, y_0) = \dfrac{\partial^2 f }{\partial x \partial y} (x_0, y_0)$$
Demostración:
Definamos $ A = f (x_0 + h, y_0 + k) \, – \, f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 + k) \, + \, f (x_0 , y_0 ) = g (x_0 + h) \, – \, g (x_0)$
Si $g (x , y_0 + k) \, – \, f (x, y_0)$, fijando $y_0, k$ tenemos que $g (x) = \dfrac{\partial f}{\partial y} (x, y_0 + \theta k) k $ con $ 0 < \theta < 1$.
Entonces
$\dfrac{\partial g}{\partial x} (x_0 + \eta h) h $ y por tanto
$ A = \dfrac{\partial }{\partial x} \dfrac{\partial f}{\partial y} (x_0 + \eta h, y_0 + \theta k) h k $
Por otra parte $A$ también puede verse como una resta de valores de otra función $G$.
$A = G ( y_0 + k) \, – \, G (y_0) $ , donde $ G (y) = f ( x_0 + h, y ) \, – \, f (x_0, y)$
Fijando $x_0 , h$
$ G ( y_0 + k) = f ( x_0 + h, y_0 + k ) \, – \, f (x_0, y_0 + k )$, y por otro lado
$G (y_0) = f ( x_0 + h, y_0 ) \, – \, f (x_0, y_0 )$
Luego
$ G ( y_0 + k) \, – \, G (y_0) = f ( x_0 + h, y_0 + k ) \, – \, f (x_0, y_0 + k ) \, – \, f ( x_0 + h, y_0 ) \, + \, f (x_0, y_0 )$
Además
$G’ ( y_0 + \hat{\theta} k) = \dfrac{G (y_0 + k) \, – \, G(y_0)}{k}$
$ k G’ ( y_0 + \hat{\theta} k) = G (y_0 + k) \, – \, G(y_0) $
Entonces
$\begin{align*} A &= G ( y_0 + k) \, – \, G (y_0) \\ &= \dfrac{ \partial G}{\partial y} (y_0 + \hat{\theta} k ) k \\ &= \Big( \dfrac{ \partial f}{\partial y} (x_0 + h , y_0 + \hat{\theta} k) k \, – \, \dfrac{ \partial f}{\partial y} (x_0 , y_0 + \hat{\theta} k) k \Big) \\ &= \dfrac{ \partial }{\partial y} \dfrac{ \partial f}{\partial y} (x_0 + \hat{\eta} h , y_0 + \hat{\theta} k) h k \end{align*}$
Entonces $ \dfrac{A}{h k} = \dfrac{ \partial }{\partial y} \dfrac{ \partial f}{\partial y} (x_0 + \hat{\eta} h , y_0 + \hat{\theta} k)$
Luego
$\lim\limits_{(h, k) \to (0, 0)} \dfrac{A}{h k} = \lim\limits_{(h, k) \to (0, 0)} \Bigg[ \dfrac{\partial^2 f}{\partial y \partial x} (x_0 + \hat{\eta} h , y_0 + \hat{\theta} k) \Bigg] = \dfrac{\partial^2 f}{\partial y \partial x} (x_0, y_0) \; \; \; _{\blacksquare}$
${}$
Teorema de Taylor ( 1° grado)
Sea $ f : U \subseteq \mathbb{R}^n \rightarrow \mathbb{R} $ , de clase $\mathcal{C}^2$ , diferenciable en $ \vec{x_0} \in U$ abierto. Entonces $$ f (\vec{x_0} + \vec{h} ) = f (\vec{x_0}) + \nabla f (\vec{x_0}) \cdot \vec{h} + R_1 (\vec{x_0}, \vec{h})$$
donde $\; \; \lim\limits_{\vec{h} \to \vec{0}} \dfrac{R_1 (\vec{x_0}, \vec{h})}{ \big\| \vec{h} \big\|} = 0$
Teorema de Taylor ( 2° grado)
Sea $ f : U \subseteq \mathbb{R}^n \rightarrow \mathbb{R} $ , de clase $\mathcal{C}^3.$ Entonces $$ f (\vec{x_0} + \vec{h} ) = f (\vec{x_0}) + \sum\limits_{i = 1}^{n} h_i \dfrac{\partial f}{\partial x_i} \vec{x_0} + \frac{1}{2} \sum\limits_{i, j = 1}^{n} h_i h_j \dfrac{\partial^2 f}{\partial x_i \partial x_j} \vec{x_0} + R_2 (\vec{x_0}, \vec{h})$$
tal que $\; \; \lim\limits_{\vec{h} \to \vec{0}} \dfrac{R_2 (\vec{x_0}, \vec{h})}{ \big\| \vec{h} \big\|^2 } = 0$ , y $ \vec{h} = (h_1 , h_2 , \cdots , h_n ).$
