Introducción
Esta es la primera entrada del curso de Geometría Moderna I el cual está basado en el temario oficial de la Facultad de Ciencias de la UNAM. Aquí presentaremos algunos conceptos básicos que nos serán de ayuda para empezar el curso.
El termino Geometría Moderna se refiere a aquella geometría deductiva, que fue desarrollada después de Euclides y hasta el desarrollo de las geometrías no euclidianas, este periodo está comprendido entre los siglos III AC y XIX DC, es decir, la geometría griega hecha con regla y compás, pero después de los griegos.
La geometría euclidiana estudia propiedades básicas de los objetos geométrico tales como punto, recta, triángulo o circunferencia, a partir de un conjunto de axiomas y de manera sintética, es decir, sin el uso de un eje de coordenadas o métodos algebraicos muy complejos, aunque si se hace uso de nociones básicas de Teoría de Conjuntos, como las de pertenencia o intersección de conjuntos.
Muchas de estas propiedades son de carácter métrico, es decir, sobre la medición de magnitudes de ángulos, longitudes de segmentos, distancias entre puntos o áreas de figuras geométricas, pero también nos hablan sobre la concurrencia de rectas (rectas diferentes que pasan por un mismo punto), colinealidad de puntos (puntos distintos que están sobre una misma recta) o puntos cíclicos (puntos distintos que están en una misma circunferencia).
Punto, recta y circunferencia
Definición 1. Un punto es la representación de un lugar específico en el plano, no tiene longitud, altura ni ninguna otra dimensión, en nuestro cuaderno o el pizarrón podemos representar este lugar con la marca más pequeña y visible que nuestro lápiz o gis puedan hacer, la cual en realidad si tiene dimensiones, pero lo que solo nos interesa es la abstracción de ese lugar marcado.
La mayoría del tiempo para referirnos a puntos emplearemos letras mayúsculas.
Definición 2. Una línea recta es un objeto de una sola dimensión, solo tiene longitud y se extiende de manera infinita en ambos sentidos, todos sus puntos se encuentran en una misma dirección de manera que dos puntos distintos determinan a una línea recta.
Nos referiremos a una línea recta simplemente como recta. Si no conocemos dos puntos por donde pasa una recta la denotaremos con la letra $l$.
Cuando la intersección de dos rectas $l_{1}$, $l_{2}$ es vacía, es decir, no tienen ningún punto en común $l_{1} \cap l_{2} = \varnothing$, decimos que son rectas paralelas y lo denotamos como $l_{1} \parallel l_{2}$.
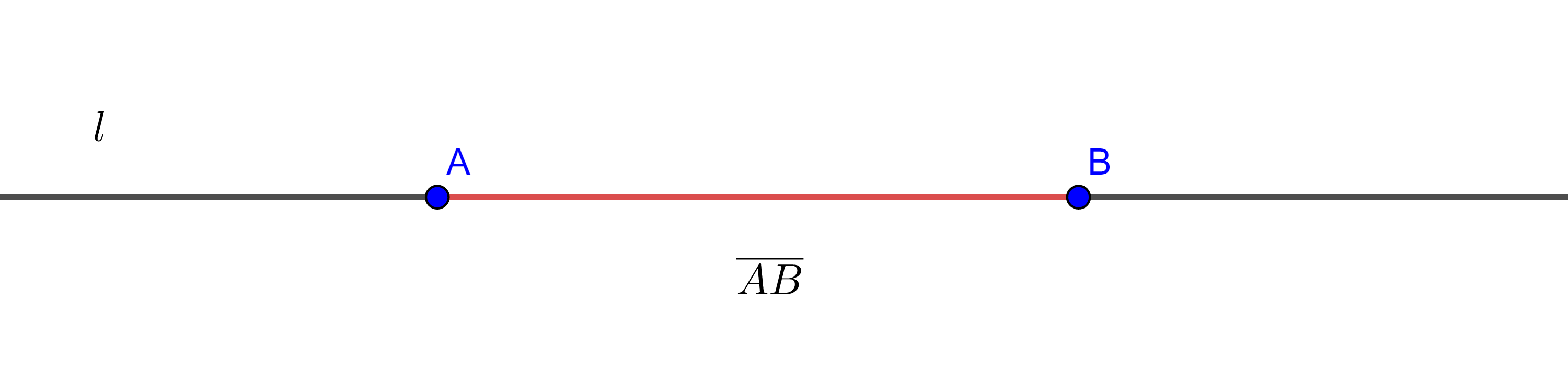
A la porción de línea recta que une dos puntos distintos en el plano (incluyendo a los puntos) y que no se extiende más allá de ellos le llamamos segmento de recta o simplemente segmento.
La distancia entre dos puntos es la magnitud del segmento de recta que los une.
Si conocemos dos puntos distintos $P$, $Q$ de una recta nos referiremos al segmento que une dichos puntos como $PQ$, en ocasiones también nos podremos referir a la recta completa con la misma notación de acuerdo al contexto del problema.
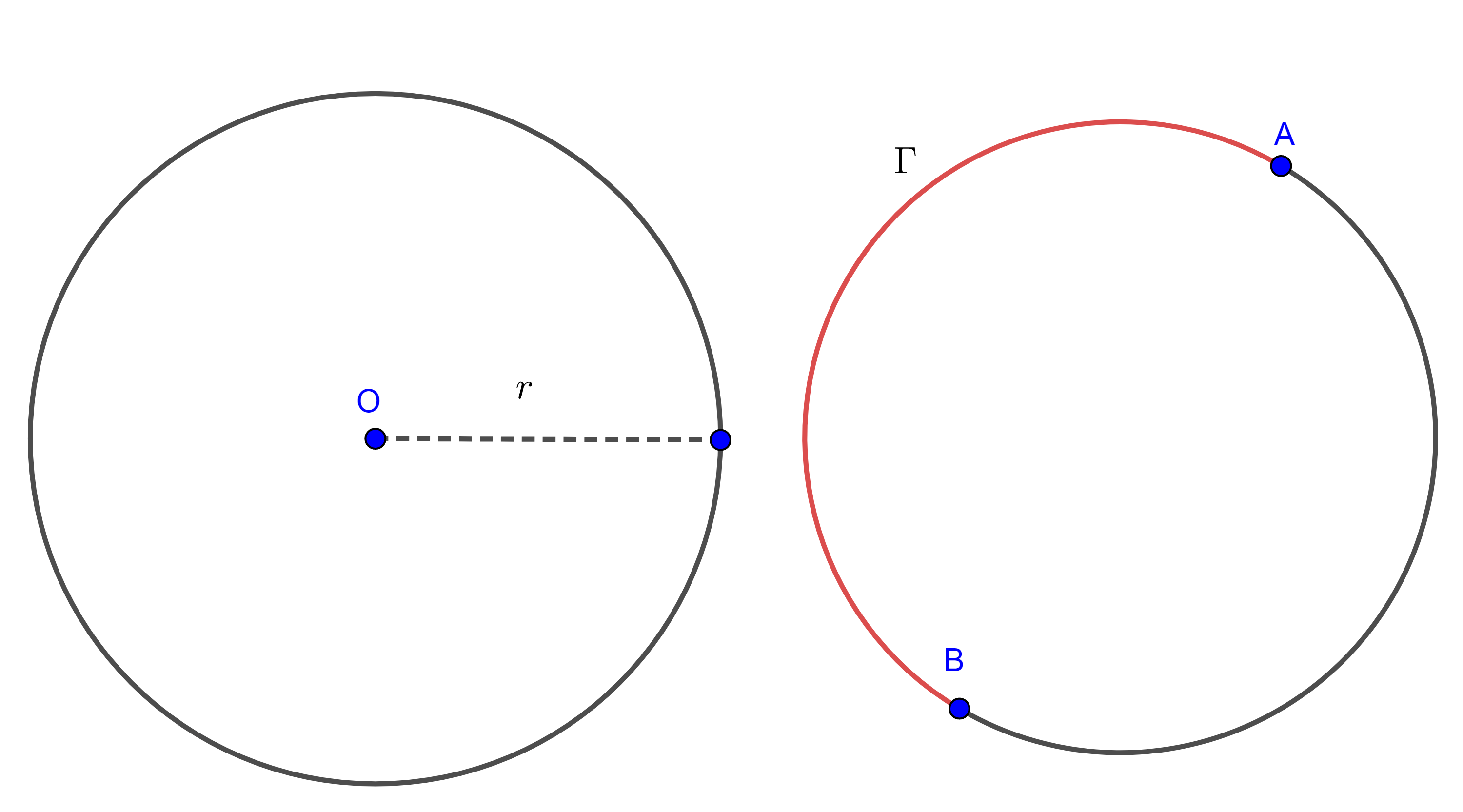
Definición 3. Dados un punto $O$ del plano y una magnitud $r \geq 0$, definimos a la circunferencia con centro en $O$ y radio $r$ $(O, r)$ como el conjunto de puntos en el plano cuya distancia al punto $O$ es $r$.
Algunas veces no nos importará o no conoceremos el centro o el radio de una circunferencia, en tal caso nos referiremos a ella con cualquier otra letra como $\Gamma$.
Al segmento que une dos puntos distintos de una circunferencia y que pasa por su centro le llamamos diámetro.
Si conocemos dos puntos $A$ y $B$ diametralmente opuestos de una circunferencia podemos denotarla como $\Gamma(AB)$.
A la porción de una circunferencia que une dos puntos distintos en ella le llamamos arco de circunferencia, para dos puntos distintos en una circunferencia $A$ y $B$, denotamos al arco recorrido de $A$ a $B$ en el sentido contrario de las manecillas del reloj como $\overset{\LARGE{\frown}}{AB}$.
Ángulo
Definición 4. Un ángulo es un objeto formado cuando dos rectas o segmentos se intersecan. Al punto en común le llamamos vértice y los segmentos o semirectas que concurren en el vértice son los lados del ángulo.
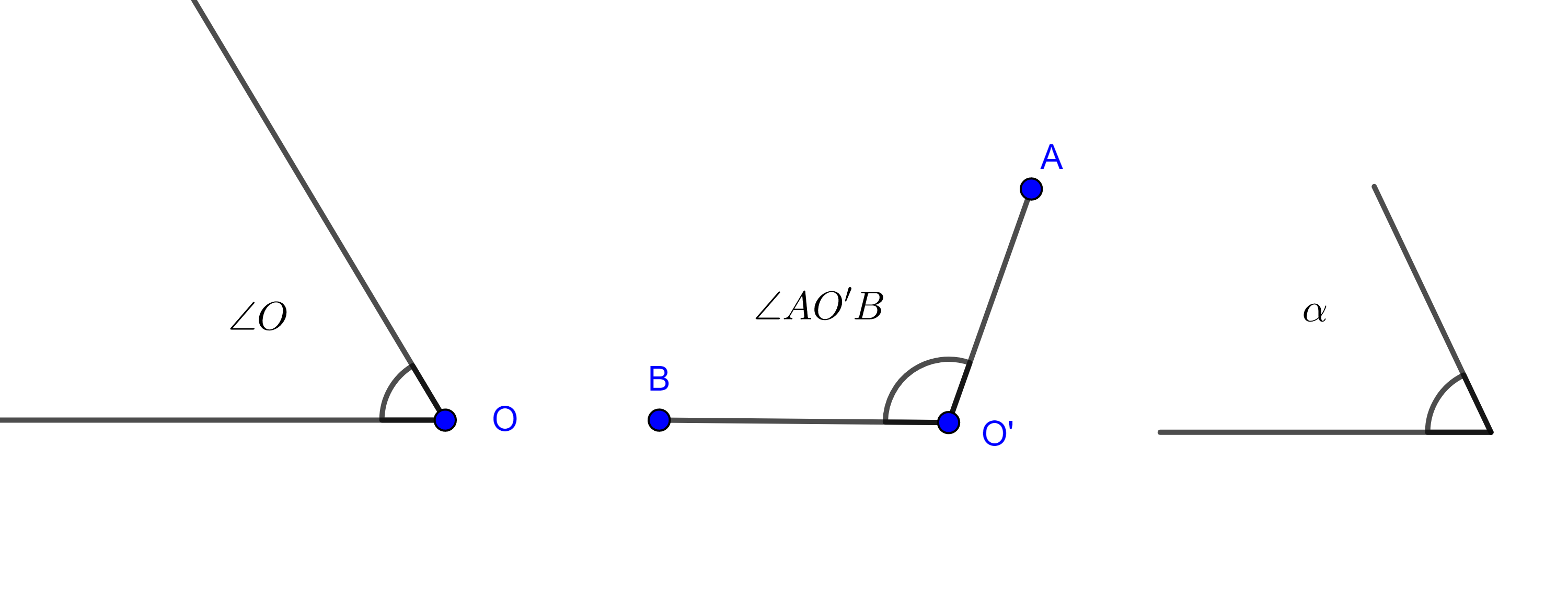
Cuando es claro cuáles son los lados de un ángulo con vértice en $O$ lo denotamos como $\angle O$.
Cuando queremos hacer énfasis en los segmentos que forman un ángulo con vértice $O’$, escribimos $\angle AO’B$ si nos referimos al desplazamiento del segmento $AO$ hacia $BO$ en contra del movimiento de las manecillas del reloj.
También podemos etiquetar a un ángulo con letras griegas minúsculas.
Cuando dos rectas o segmentos distintos se intersecan se forman cuatro ángulos, en este caso a los ángulos que comparten un lado en común les llamamos adyacentes y a los que no tienen un lado en común, opuestos por el vértice.
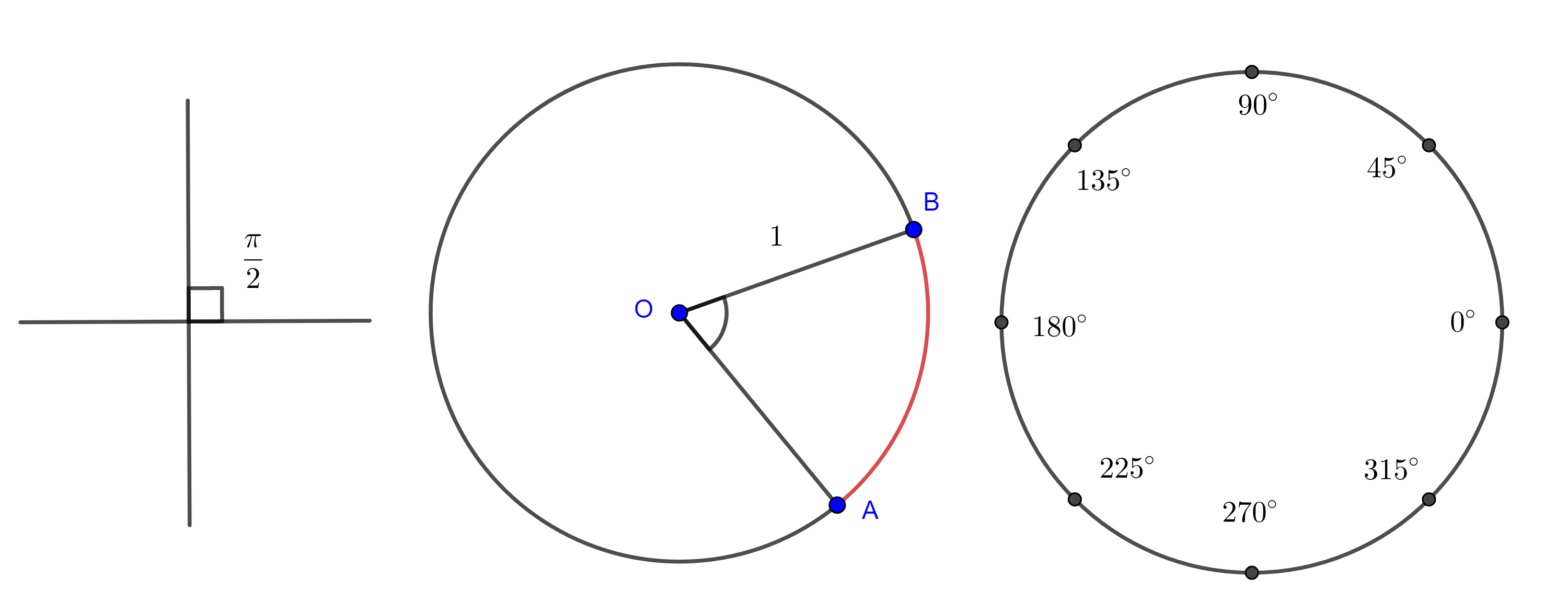
Decimos que un ángulo es recto si es aquel que se obtiene cuando dos rectas $l_{1}$, $l_{2}$ se intersecan formando cuatro ángulos iguales y en este caso decimos que las rectas son perpendiculares $l_{1} \perp l_{2}$. Denotamos a la suma de dos ángulos rectos como $\pi$.
Para medir la magnitud de un ángulo $\angle O$ trazamos una circunferencia de radio $1$ con centro en el vértice del ángulo y ubicamos las intersecciones de los lados del ángulo con la circunferencia digamos $A$ y $B$, entonces la medida de $\angle AOB$ será la magnitud del arco $\overset{\LARGE{\frown}}{AB}$.
En calculo se muestra que $\pi = 3.14159…$, es un numero irracional, esto es, su representación decimal es infinita y no periódica.
Otra forma de medir los ángulos es dividir a la circunferencia en $360$ partes iguales o grados, de esto se sigue que $\dfrac{\pi}{2} = 90^{\circ}$, $\pi = 180^{\circ}$, $2\pi = 360^{\circ}$.
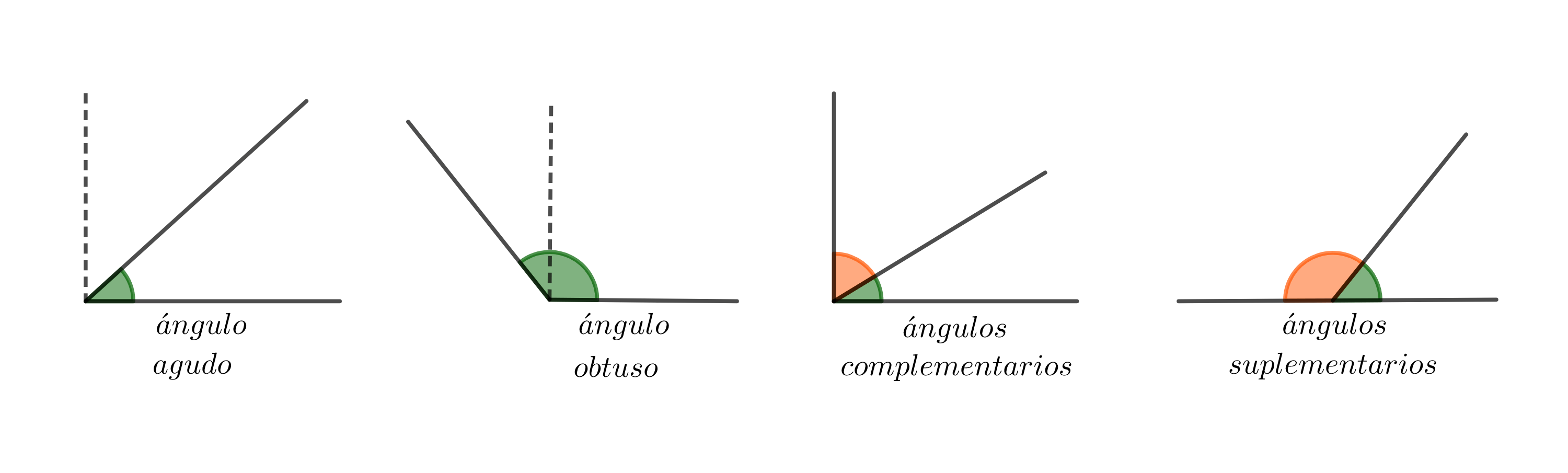
Un ángulo que es menor que uno recto es un ángulo agudo y uno que es mayor a uno recto se llama ángulo obtuso.
Dos ángulos que suman $\dfrac{\pi}{2}$ son complementarios y dos ángulos cuya suma es igual a $\pi$ se llaman suplementarios.
Triángulo
Definición 5. Un triángulo es una figura en el plano que consiste de tres puntos distintos, llamados vértices, que no son colineales, y por los segmentos que unen dichos vértices a los que llamamos lados del triángulo.
Si los vértices de un triangulo son $A$, $B$ y $C$, denotamos al triángulo como $\triangle ABC$ recorriendo los vértices en el sentido contrario de las manecillas del reloj.
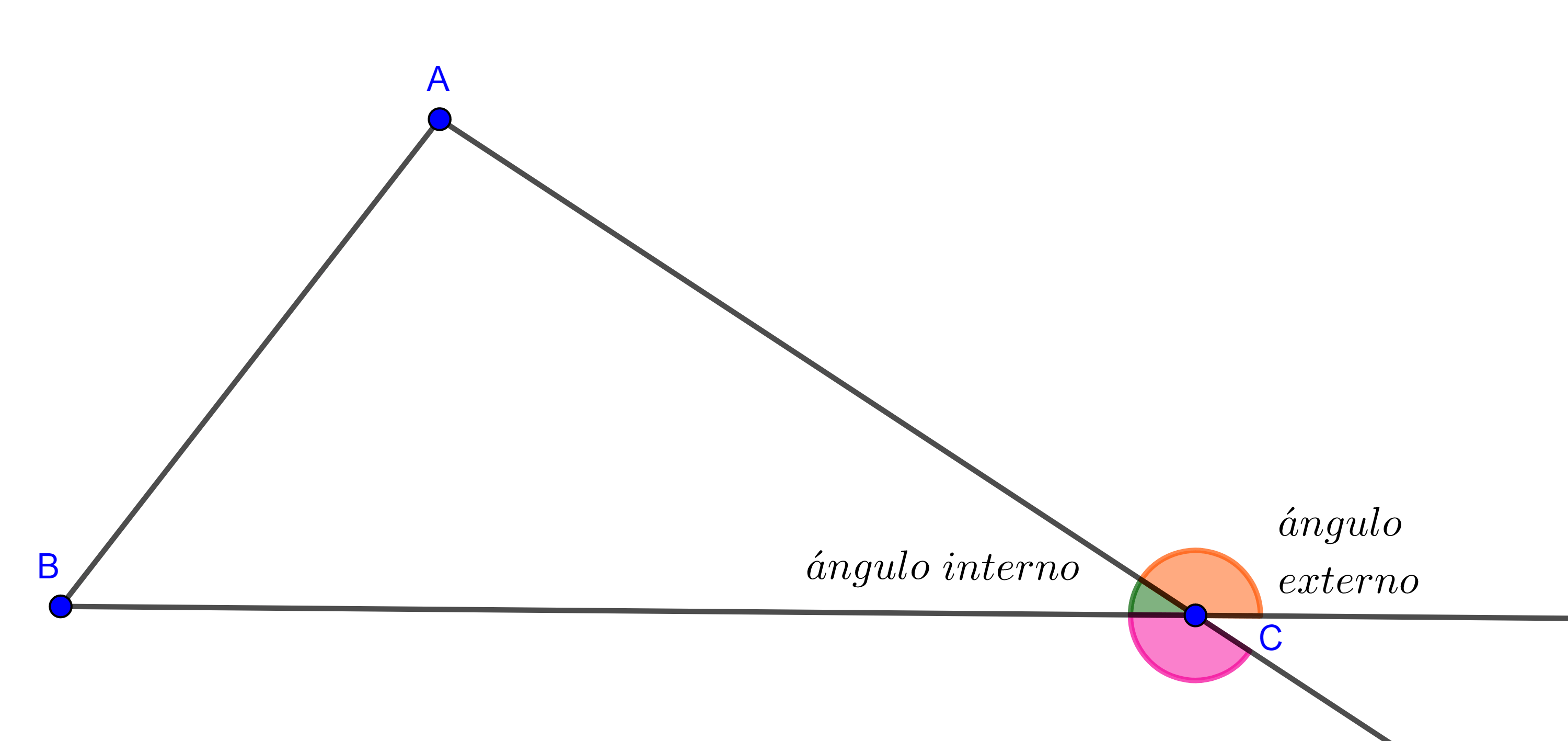
Recordemos leer los ángulos en el sentido contrario al de las manecillas del reloj. A $\angle BAC$, $\angle CBA$ y $\angle ACB$ les llamamos ángulos internos o interiores.
Si extendemos los lados del triángulo, a los ángulos que son suplementarios a los ángulos interiores les llamamos ángulos exteriores o externos, notemos que por cada ángulo interno hay dos externos.
Clasificamos a los triángulos de acuerdo a la magnitud de sus lados y de sus ángulos internos.
De acuerdo a sus lados:
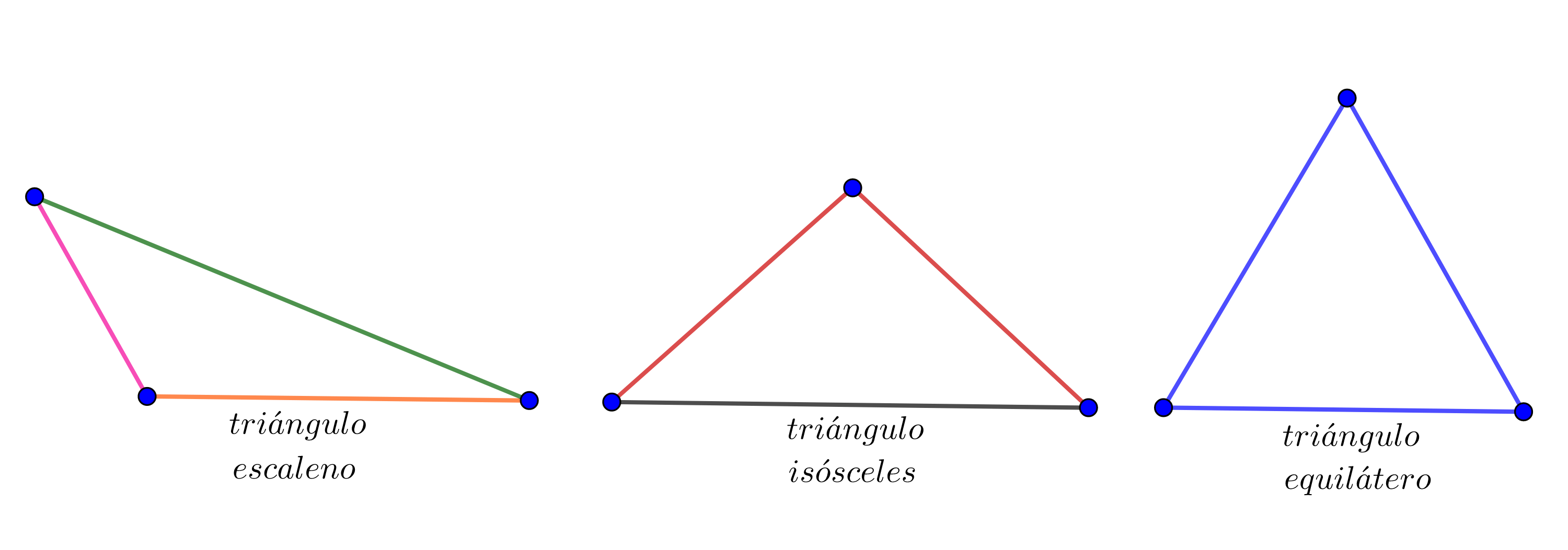
escaleno, si ningún par de lados es igual,
isósceles, si tienen dos lados iguales,
equilátero, si todos sus lados son iguales.
De acuerdo a sus ángulos internos:
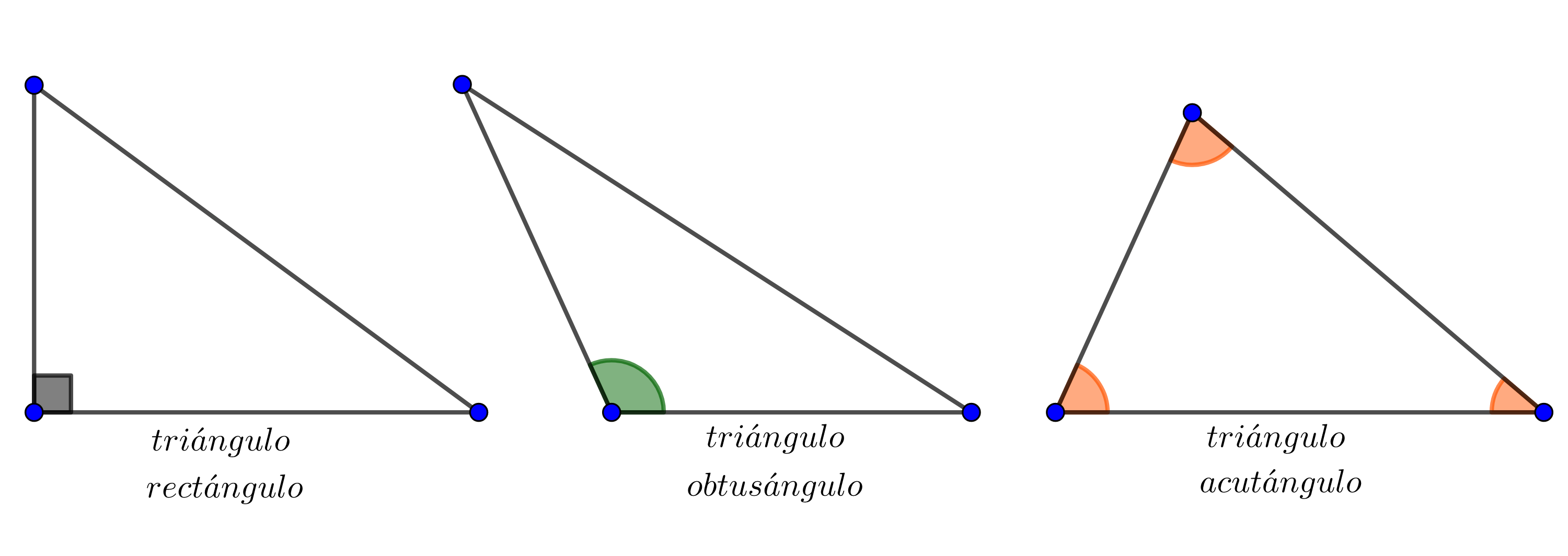
rectángulo, si un ángulo interno es recto,
acutángulo, si todos sus ángulos internos son agudos,
obtusángulo, si uno de sus ángulos internos es obtuso.
Problema. Dado un segmento construir sobre él un triángulo equilátero.
Solución. Para hacer una construcción geométrica usamos una regla sin graduar y un compás. La regla nos permite trazar la recta que une cualesquiera dos puntos distintos y con el compás podemos trazar circunferencias conociendo su centro y radio.
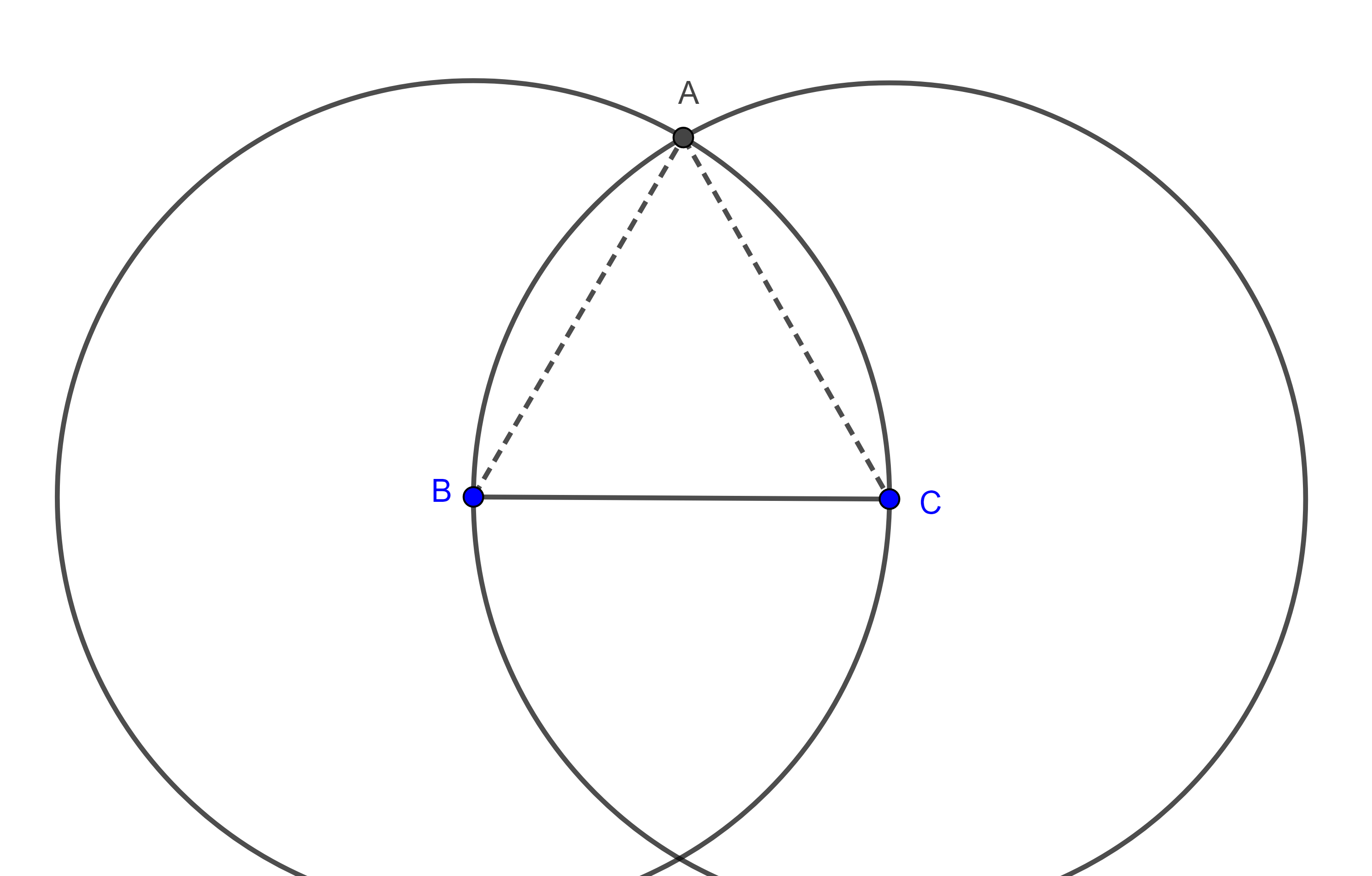
Sea $BC$ el segmento dado, trazamos dos circunferencias de radio $BC$, una con centro en $B$ y otra con centro en $C$.
Sea $A$ la intersección de $(B, BC)$ con $(C, BC)$, trazamos $AB$ y $AC$, entonces $AB = BC$, por ser radios de $(B, BC)$ y $AC = BC$, por ser radios de $(C, BC)$.
Por lo tanto, $AB = BC = AC$ y así $\triangle ABC$ es equilátero.
$\blacksquare$
El triángulo es uno de los objetos más estudiados en geometría euclidiana. En las próximas entradas abordaremos teoremas fundamentales acerca del triángulo como los de congruencia, semejanza o el teorema de Pitágoras.
Más adelante…
En la siguiente entrada presentaremos los postulados de Euclides que son el punto de partida para poder establecer relaciones entre los objetos que hemos definido.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Muestra que los ángulos opuestos por el vértice son iguales.
- Convierte a grados los siguientes ángulos: $\dfrac{\pi}{3}$, $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$.
- Calcula la longitud de arco de los siguientes ángulos: $225^{\circ}$, $270^{\circ}$, $315^{\circ}$.
- Dados dos segmentos de distinta longitud, construir sobre el mayor un segmento de igual magnitud al menor.
- GeoGebra es un software libre de matemáticas muy útil, con él te puedes apoyar para hacer tus demostraciones durante este curso, aquí esta la versión online.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Siguiente entrada del curso: Postulados de Euclides.
- Otros cursos.
Fuentes
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 1-6.
- Math Open Reference
- Geometría interactiva
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»