Archivo de la etiqueta: sistemas lineales

Ecuaciones Diferenciales I: Linealización de los puntos de equilibrio de sistemas no lineales

Por Omar González Franco

La educación en matemáticas es mucho más complicada que lo que esperabas,
incluso si esperabas que es más complicada que lo que esperabas.
– Edward Griffith Begle

Introducción

Nos acercamos al final de este curso. Para concluir estudiaremos un último tema que tiene que ver con los sistemas autónomos de ecuaciones diferenciales no lineales.

Resolver de forma analítica sistemas de ecuaciones diferenciales no lineales puede ser una tarea sumamente complicada y en algunos casos hasta imposible, es por ello que en muchas ocasiones se opta por resolverlos con métodos numéricos. En este curso no veremos métodos numéricos y mucho menos métodos analíticos para resolver sistemas de ecuaciones diferenciales no lineales debido a que requerimos de más teoría que queda fuera de este primer curso de ecuaciones diferenciales. Pero lo que si podemos hacer es un análisis cualitativo como lo hemos estado haciendo en esta unidad.

Recordemos que el espacio fase de un sistema de ecuaciones diferenciales aporta la suficiente información como para conocer de forma completa el comportamiento de los soluciones a diferentes tiempos, incluso esta información puede ser suficiente para describir el fenómeno que estemos estudiando sin la necesidad de conocer explícitamente las soluciones del sistema.

En esta y las próximas entradas comenzaremos a desarrollar métodos cualitativos que nos permitirán construir el espacio fase de sistemas no lineales y por tanto conocer el comportamiento de sus soluciones a diferentes tiempos y diferentes condiciones iniciales.

En estos momentos ya conocemos métodos analíticos y geométricos que nos permiten entender completamente a los sistemas lineales, es posible combinar estos métodos con algunas otras técnicas cualitativas adicionales para describir a los sistemas no lineales. Comenzaremos desarrollando el método de linealización, el cual nos mostrará cómo es que puede aproximarse un sistema no lineal a un punto de equilibrio por medio de un sistema lineal.

Trayectorias de los sistemas no lineales

Consideremos el siguiente sistema no lineal.

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + (1 -x^{2})y \label{1} \tag{1}
\end{align*}

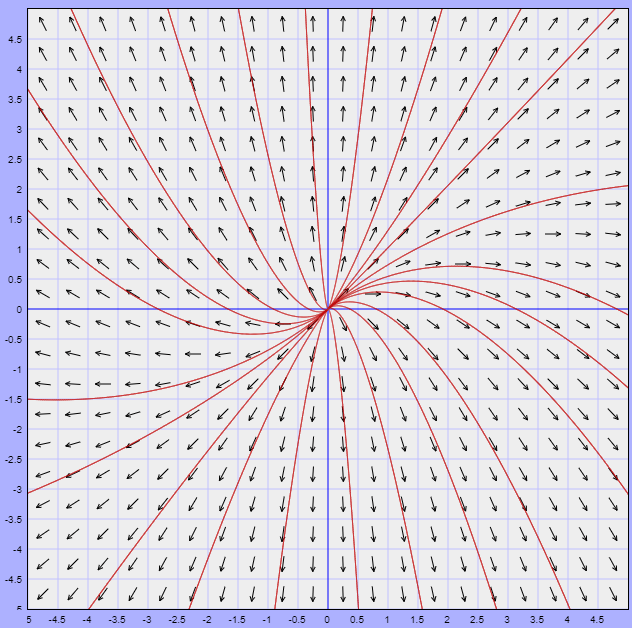
Enseguida podemos darnos cuenta de que el único punto de equilibrio del sistema es el origen. Usando la herramienta que hemos estado utilizando a lo largo de esta unidad podemos visualizar el plano fase del sistema acompañado del campo vectorial asociado.

Las trayectorias en general no muestran un comportamiento parecido a alguno de los sistemas estudiados en las entradas anteriores y claro que debe ser así, ya que en este caso se trata de un sistema no lineal. Sin embargo, se puede notar que alrededor del punto de equilibrio, es decir del origen, si hay un comportamiento que nos parece familiar, pues se trata de una espiral que se aleja del origen (parecido a foco inestable).

Lo que haremos será aproximar el sistema (\ref{1}) con un sistema que sea mucho más fácil de analizar. Observemos que el término que hace que el sistema no sea lineal es $x^{2}y$ en la ecuación para $y^{\prime}$. Si $x$ y $y$ son pequeñas (cercanas al punto de equilibrio), entonces el término $x^{2}y$ es aún mucho más pequeño, de manera que para valores pequeños de $x$ y de $y$ es posible aproximar el sistema (\ref{1}) en un sistema lineal en el que no aparece el término $x^{2}y$, dicho sistema es

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + y \label{2} \tag{2}
\end{align*}

Ambos sistemas deben ser muy similares en una vecindad muy próxima al punto de equilibrio, en este caso en el origen. Veamos el plano fase del sistema lineal (\ref{2}).

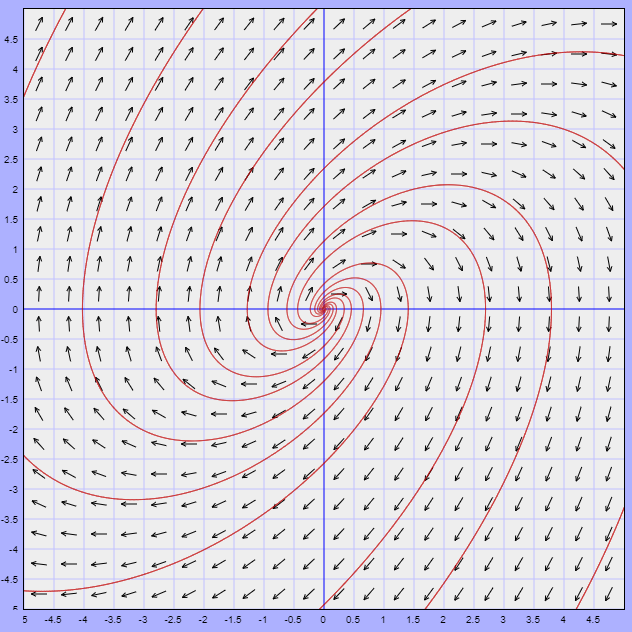
Si observamos con cuidado ambos planos fase vemos que efectivamente son muy similares alrededor del origen, ya que ambos corresponden a espirales que se alejan del origen.

El plano fase del sistema (\ref{2}) corresponde a un sistema con valores propios complejos. Prueba que efectivamente los valores propios son

$$\lambda_{1} = \dfrac{1 + i \sqrt{3}}{2} \hspace{1cm} y \hspace{1cm} \lambda_{2} = \dfrac{1 -i \sqrt{3}}{2}$$

Como son complejos con parte real positiva, sabemos que las soluciones del sistema lineal se mueven en espiral alejándose del origen.

Lo que hemos hecho se conoce como linealización del punto de equilibrio. Cerca del punto de equilibrio aproximamos el sistema no lineal por medio de un sistema lineal apropiado. Para condiciones iniciales cerca del punto de equilibrio las soluciones del sistema no lineal y de la aproximación lineal permanecen cercanas entre sí, por lo menos en algún intervalo.

El sistema no lineal (\ref{1}) se conoce como ecuación de Van der Pol y más adelante volveremos a él.

Veamos cómo sería hacer una linealización de un sistema no polinomial. Consideremos el sistema no lineal

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -y -\sin(x) \label{3} \tag{3}
\end{align*}

El término no lineal corresponde a la función seno. Este modelo bien puede representar el movimiento de un péndulo amortiguado.

Los puntos de equilibrio del sistema son $Y_{0} = (0, 0), (\pm \pi, 0), (\pm 2\pi, 0)$, etcétera. Concentrémonos sólo en el origen.

Sabemos que

$$\sin(x) = x -\dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} – \cdots \label{4} \tag{4}$$

Entonces podemos escribir al sistema (\ref{3}) como

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -y -\left( x -\dfrac{x^{3}}{3!} + \dfrac{x^{5}}{5!} – \cdots \right) \label{5} \tag{5}
\end{align*}

Para $x$ muy pequeña los términos con potencia son aún más pequeños, así que los podemos omitir aproximándonos al siguiente sistema lineal.

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -y -x \label{6} \tag{6}
\end{align*}

Los valores propios de este sistema son

$$\lambda_{1} = \dfrac{-1 + i \sqrt{3}}{2} \hspace{1cm} y \hspace{1cm} \lambda_{2} = \dfrac{-1 -i \sqrt{3}}{2}$$

Como estos números son complejos con parte real negativa, esperamos que el correspondiente punto de equilibrio para el sistema no lineal sea un foco estable.

A continuación se muestra el plano fase del sistema no lineal (\ref{3}) y posteriormente el plano fase del sistema linealizado (\ref{6}) y observemos en ambos el comportamiento de las trayectorias alrededor del punto de equilibrio $Y_{0} = (0, 0)$.

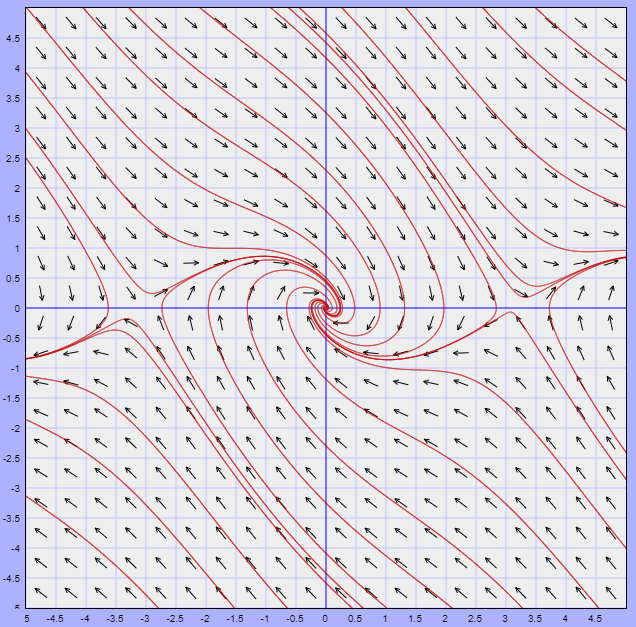
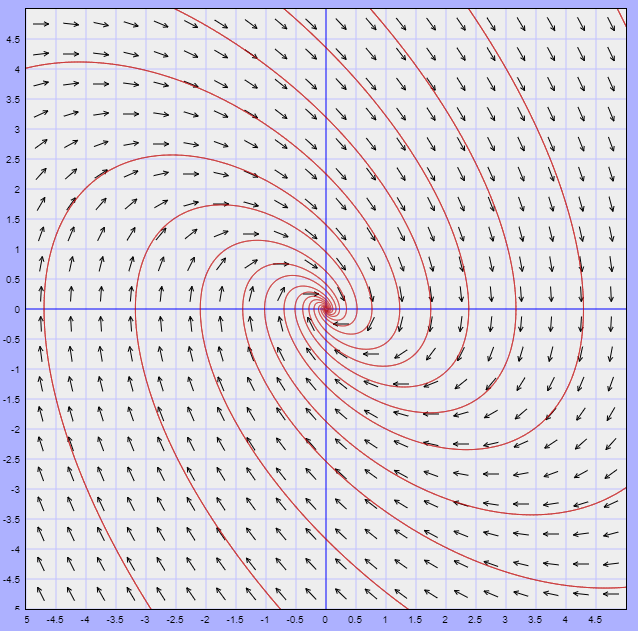
Efectivamente, en ambos planos fase alrededor del origen presentan el mismo comportamiento correspondiente a un foco estable.

El proceso de linealización puede ser directo independientemente del sistema no lineal que tengamos, pero debemos apoyarnos de una herramienta del cálculo diferencial conocida como matriz Jacobiana.

Linealización de los puntos de equilibrio

Consideremos el siguiente sistema autónomo no lineal.

\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y) \label{7} \tag{7}
\end{align*}

Supongamos que $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio de este sistema (no necesariamente el origen). Queremos entender qué sucede con las soluciones cerca de $Y_{0}$, es decir, linealizar el sistema cerca de $Y_{0}$. Introducimos nuevas variables.

\begin{align*}
u &= x -x_{0} \\
v &= y -y_{0} \label{8} \tag{8}
\end{align*}

Lo que hacen estas variables es mover el punto de equilibrio al origen. Si $x$ y $y$ están cerca del punto de equilibrio $(x_{0}, y_{0})$, entonces $u$ y $v$ tienden a $0$.

Como los números $x_{0}$ y $y_{0}$ son constantes y además

$$x = u + x_{0} \hspace{1cm} y \hspace{1cm} y = v + y_{0}$$

entonces el sistema (\ref{7}) escrito en términos de $u$ y $v$ es

\begin{align*}
\dfrac{du}{dt} &= \dfrac{d(x -x_{0})}{dt} = \dfrac{dx}{dt} = F_{1}(x, y) = F_{1}(x_{0} + u, y_{0} + v) \\
\dfrac{dv}{dt} &= \dfrac{d(y -y_{0})}{dt} = \dfrac{dy}{dt} = F_{2}(x, y) = F_{2}(x_{0} + u, y_{0} + v)
\end{align*}

Esto es,

\begin{align*}
u^{\prime} &= F_{1}(x_{0} + u, y_{0} + v) \\
v^{\prime} &= F_{2}(x_{0} + u, y_{0} + v) \label{9} \tag{9}
\end{align*}

Si $u = v = 0$, entonces

\begin{align*}
u^{\prime} &= F_{1}(x_{0}, y_{0}) \\
v^{\prime} &= F_{2}(x_{0}, y_{0})
\end{align*}

Pero,

$$F_{1}(x_{0}, y_{0}) = 0 \hspace{1cm} y \hspace{1cm} F_{2}(x_{0}, y_{0}) = 0$$

ya que $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio, esto nos muestra que hemos movido el punto de equilibrio al origen en el plano $UV$.

Lo que haremos a continuación es apoyarnos de algunos resultados del curso de Cálculo III. Necesitamos eliminar los términos de orden superior o no lineales del sistema (\ref{9}). Como esas expresiones pueden incluir funciones exponenciales, logarítmicas y trigonométricas, no siempre es claro cuáles son los términos lineales. En este caso es necesario estudiar a $F_{1}$ y $F_{2}$ con más atención.

De cálculo sabemos que es posible estudiar una función analizando su mejor aproximación lineal, la cual está dada por el plano tangente para funciones de dos variables, es decir

$$F_{1}(x_{0} + u, y_{0} + v) \approx F_{1}(x_{0}, y_{0}) + \left[ \dfrac{\partial F_{1}}{\partial x}(x_{0}, y_{0}) \right]u + \left[ \dfrac{\partial F_{1}}{\partial y}(x_{0}, y_{0}) \right]v \label{10} \tag{10}$$

El lado derecho es la ecuación para el plano tangente a la gráfica de $F_{1}$ en $Y_{0} = (x_{0}, y_{0})$. Recordemos que la expresión (\ref{10}) es también la aproximación polinomial de primer grado de Taylor para $F_{1}$.

Podemos, entonces, reescribir el sistema (\ref{9}) como

\begin{align*}
u^{\prime} &= F_{1}(x_{0}, y_{0}) + \left[ \dfrac{\partial F_{1}}{\partial x}(x_{0}, y_{0}) \right]u + \left[ \dfrac{\partial F_{1}}{\partial y}(x_{0}, y_{0}) \right]v + \vartheta_{F_{1}} \\
v^{\prime} &= F_{2}(x_{0}, y_{0}) + \left[ \dfrac{\partial F_{2}}{\partial x}(x_{0}, y_{0}) \right]u + \left[ \dfrac{\partial F_{2}}{\partial y}(x_{0}, y_{0}) \right]v + \vartheta_{F_{2}} \label{11} \tag{11}
\end{align*}

Donde $\vartheta_{F_{1}}$ y $\vartheta_{F_{2}}$ son los términos que forman la diferencia entre el plano tangente y las funciones $F_{1}$ y $F_{2}$, respectivamente, y son precisamente los términos que deseamos ignorar al formar la aproximación lineal del sistema.

Como $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio, entonces

$$F_{1}(x_{0}, y_{0}) = 0 \hspace{1cm} y \hspace{1cm} F_{2}(x_{0}, y_{0}) = 0$$

Así, las funciones (\ref{11}) se pueden aproximar como

\begin{align*}
u^{\prime} &\approx \left[ \dfrac{\partial F_{1}}{\partial x}(x_{0}, y_{0}) \right]u + \left[ \dfrac{\partial F_{1}}{\partial y}(x_{0}, y_{0}) \right]v \\
v^{\prime} &\approx \left[ \dfrac{\partial F_{2}}{\partial x}(x_{0}, y_{0}) \right]u + \left[ \dfrac{\partial F_{2}}{\partial y}(x_{0}, y_{0}) \right]v \label{12} \tag{12}
\end{align*}

Si usamos la notación matricial podemos escribir el sistema anterior como

$$\begin{pmatrix}
u^{\prime} \\ v^{\prime}
\end{pmatrix} \approx \begin{pmatrix}
\dfrac{\partial F_{1}}{\partial x}(x_{0}, y_{0}) & \dfrac{\partial F_{1}}{\partial y}(x_{0}, y_{0}) \\ \dfrac{\partial F_{2}}{\partial x}(x_{0}, y_{0})
& \dfrac{\partial F_{2}}{\partial y}(x_{0}, y_{0})
\end{pmatrix} \begin{pmatrix}
u \\ v
\end{pmatrix} \label{13} \tag{13}$$

La matriz de $2 \times 2$ de las derivadas parciales en esta expresión se llama matriz Jacobiana del sistema en $Y_{0} = (x_{0}, y_{0})$.

$$\mathbf{J}(x_{0}, y_{0}) = \begin{pmatrix}
\dfrac{\partial F_{1}}{\partial x}(x_{0}, y_{0}) & \dfrac{\partial F_{1}}{\partial y}(x_{0}, y_{0}) \\ \dfrac{\partial F_{2}}{\partial x}(x_{0}, y_{0})
& \dfrac{\partial F_{2}}{\partial y}(x_{0}, y_{0})
\end{pmatrix} \label{14} \tag{14}$$

Por lo tanto, el sistema linealizado en el punto de equilibrio $Y_{0} = (x_{0},y_{0})$ es

$$\begin{pmatrix}
u^{\prime} \\ v^{\prime}
\end{pmatrix} = \mathbf{J} \begin{pmatrix}
u \\ v
\end{pmatrix} \label{15} \tag{15}$$

Una observación importante de este proceso es que para crear el sistema linealizado sólo es necesario conocer las derivadas parciales de las componentes $F_{1}$ y $F_{2}$ del campo vectorial en el punto de equilibrio $Y_{0}$, no es necesario hacer el cambio de variable moviendo el punto de equilibrio al origen. Más adelante veremos ejemplos para mostrar este hecho.

Clasificación de los puntos de equilibrio

El método de linealización tiene como propósito usar un sistema lineal para predecir el comportamiento de las soluciones de un sistema no lineal cerca de un punto de equilibrio. En una vecindad de dicho punto, las soluciones de los sistemas lineales y no lineales están cercanas entre sí, por lo menos en un intervalo corto. Para la mayor parte de los sistemas, la información ganada al estudiar la linearización es suficiente para determinar el comportamiento a largo plazo de las soluciones del sistema no lineal cerca del punto de equilibrio.

Esta vez no seremos explícitos, pero es posible hacer una clasificación de los puntos de equilibrio en base a los valores propios de la matriz Jacobiana (\ref{14}).

Si todos los valores propios de $\mathbf{J}$ son números reales negativos o números complejos con parte real negativa, entonces $(u, v) = (0, 0)$ es un nodo atractor para el sistema lineal y todas las soluciones se acercan a $(u, v) = (0, 0)$ cuando $t \rightarrow \infty$. Para el sistema no lineal, las soluciones que empiezan cerca del punto de equilibrio $(x, y) = (x_{0}, y_{0})$ se acercan a éste cuando $t \rightarrow \infty$. Por tanto, decimos que $(x_{0}, y_{0})$ es un nodo atractor. Si los valores propios son complejos, entonces $(x_{0}, y_{0})$ es un foco estable.

De modo similar, si $\mathbf{J}$ sólo tiene valores propios positivos o complejos con parte real positiva, entonces las soluciones con condiciones iniciales cerca del punto de equilibrio $(x_{0}, y_{0})$ tienden a alejarse de éste cuando $t$ crece. Decimos entonces que para un sistema no lineal el punto $(x_{0}, y_{0})$ es una nodo repulsor. Si los valores propios son complejos, entonces $(x_{0}, y_{0})$ es un foco inestable.

Si $\mathbf{J}$ tiene un valor propio positivo y uno negativo, entonces el punto de equilibrio $(x_{0}, y_{0})$ es un punto silla.

Es importante mencionar que esta clasificación de los puntos de equilibrio para los sistemas no lineales no nos dice nada acerca del comportamiento de las soluciones con posiciones iniciales lejanas del punto de equilibrio $(x_{0}, y_{0})$.

Para concluir con esta entrada realicemos algunos ejemplos.

Ejemplo: Linealizar el siguiente sistema no lineal.

\begin{align*}
x^{\prime} &= x(2 -x -y) \\
y^{\prime} &= -x + 3y -2xy
\end{align*}

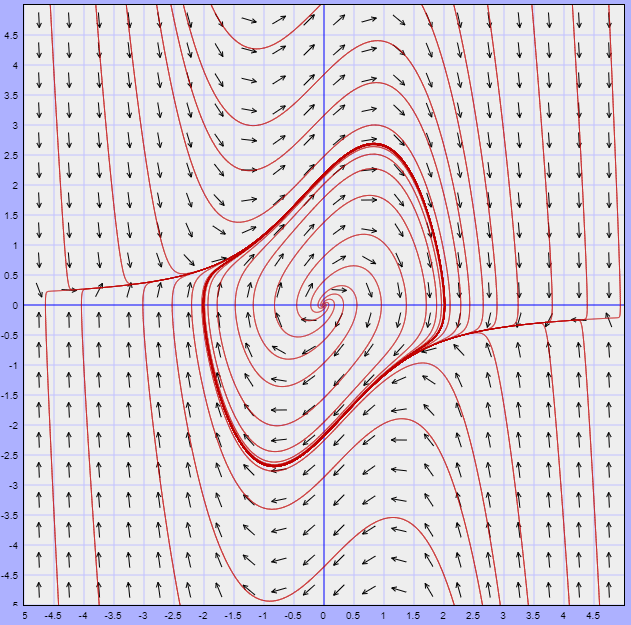
Solución: Comencemos por observar el plano fase de este sistema no lineal.

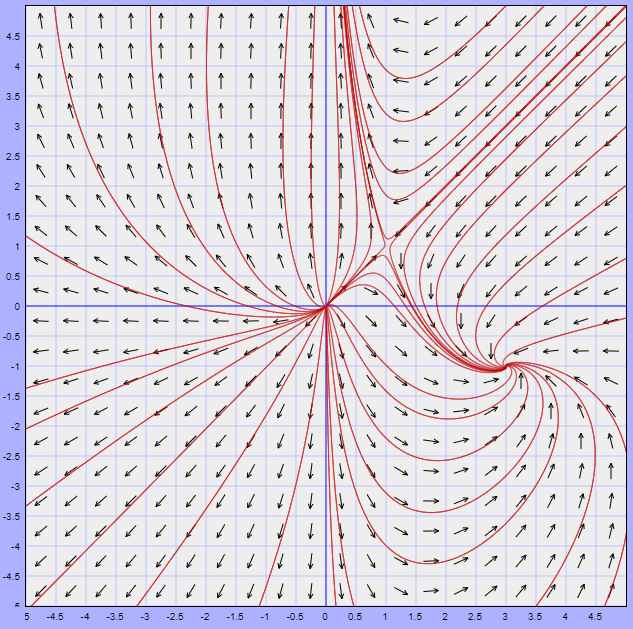
Nota: Cuando estudiamos las propiedades cualitativas de las trayectorias vimos que es posible esbozar el plano fase de un sistema no lineal si resolvemos la ecuación diferencial

$$\dfrac{dy}{dx} = \dfrac{F_{2}(x, y)}{F_{1}(x, y)} \label{16} \tag{16}$$

pero no siempre obtendremos una ecuación sencilla de resolver. En general, aún no sabemos cómo esbozar el plano fase de un sistema no lineal, lo ideal es que nosotros lo pudiéramos hacer a mano. Por ahora sólo nos estaremos apoyando de un programa que nos permite obtenerlo, más adelante veremos cómo esbozarlo no sólo cerca de los puntos de equilibrio.

Continuemos con el ejemplo. Del plano fase podemos observar que los puntos de equilibrio son

$$Y_{0} = (0, 0), \hspace{1cm} Y_{1} = (1, 1) \hspace{1cm} y \hspace{1cm} Y_{2} = (3, -1)$$

Veamos que es así analíticamente y linealicemos cada uno de ellos.

La función vectorial $F(x, y)$ que define al campo vectorial es

$$F(x, y) = (x(2 -x -y), -x + 3y -2xy)$$

Vemos que las funciones $F_{1}(x, y)$ y $F_{2}(x, y)$ son

\begin{align*}
F_{1}(x, y) &= x(2 -x -y) \\
F_{2}(x, y) &= -x + 3y -2xy
\end{align*}

No es necesario hacer algún tipo de cambio de variable, directamente podemos determinar la matriz Jacobiana para obtener una expresión similar a (\ref{15}). Calculemos las derivadas parciales de $F_{1}(x, y)$ y $F_{2}(x, y)$.

$$\dfrac{\partial F_{1}}{\partial x} = 2 -2x -y, \hspace{1cm} \dfrac{\partial F_{1}}{\partial y} = -x, \hspace{1cm} \dfrac{\partial F_{2}}{\partial x} = -1 -2y, \hspace{1cm} \dfrac{\partial F_{2}}{\partial y} = 3 -2x$$

Por lo tanto, la matriz Jacobiana es

$$\mathbf{J}(x, y) = \begin{pmatrix}
2 -2x -y & -x \\ -1 -2y & 3 -2x
\end{pmatrix}$$

Por otro lado, determinemos los puntos de equilibrio. Buscamos los valores de $x$ y $y$, tal que

$$F_{1}(x, y) = 0 \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = 0$$

es decir,

\begin{align*}
x(2 -x -y) &= 0 \\
-x + 3y -2xy &= 0
\end{align*}

De la primer ecuación obtenemos que $x = 0$ y $2 -x -y = 0$, de este segundo resultado vemos que $x = 2 -y$, sustituyamos ambos valores en la segunda ecuación.

Para $x =0$ obtenemos $3y =0$, de donde $y =0$. Por lo tanto, el origen es un punto de equilibrio.

Para $x =2 -y$, tenemos

$$-(2 -y) + 3y -2(2 -y)y =y^{2} -1 = 0$$

De donde $y_{1} = 1$ y $y_{2} = -1$, sustituyendo ambas raíces en $x = 2 -y$, se tiene

\begin{align*}
x_{1} &= 2 -1 = 1 \\
x_{2} &= 2 -( -1) = 3
\end{align*}

Por lo tanto, los puntos de equilibrio son

$$Y_{0} = (0, 0), \hspace{1cm} Y_{1} = (1, 1) \hspace{1cm} y \hspace{1cm} Y_{2} = (3, -1)$$

tal como lo indica el plano fase.

Linealicemos el sistema, para ello evaluemos cada punto de equilibrio en la matriz Jacobiana.

$$\mathbf{J}(0, 0) = \begin{pmatrix}
2 & 0 \\ -1 & 3
\end{pmatrix}, \hspace{1cm} \mathbf{J}(1, 1) = \begin{pmatrix}
-1 & -1 \\ -3 & 1
\end{pmatrix}, \hspace{1cm} \mathbf{J}(3, -1) = \begin{pmatrix}
-3 & -3 \\ 1 & -3
\end{pmatrix}$$

Por lo tanto, alrededor del punto de equilibrio $Y_{0} = (0, 0)$ el sistema no lineal puede ser descrito por el sistema lineal

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 0 \\ -1 & 3
\end{pmatrix}\mathbf{Y}$$

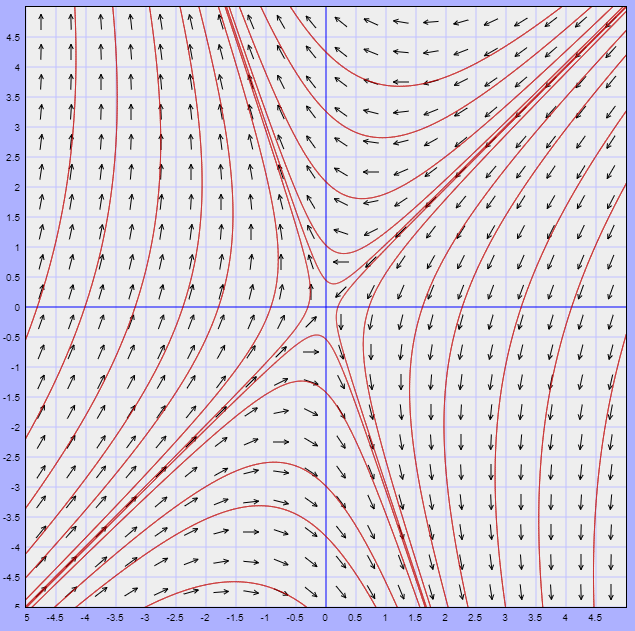
Plano fase del sistema linealizado en el punto de equilibrio $Y_{0} = (0, 0)$.

Alrededor del punto de equilibrio $Y_{0} = (1, 1)$ el sistema no lineal puede ser descrito por el sistema lineal

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & -1 \\ -3 & 1
\end{pmatrix} \mathbf{Y}$$

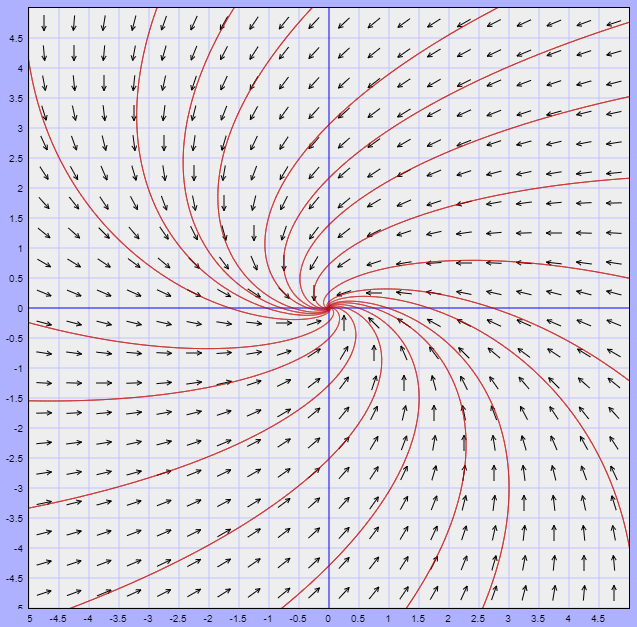
Plano fase del sistema linealizado en el punto de equilibrio $Y_{0} = (1, 1)$.

Y finalmente el sistema no lineal, alrededor del punto de equilibrio $Y_{0} = (3, -1)$, puede ser descrito por el sistema lineal

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-3 & -3 \\ 1 & -3
\end{pmatrix} \mathbf{Y}$$

Plano fase del sistema linealizado en el punto de equilibrio $Y_{0} = (3, -1)$.

Por su puesto que se puede aplicar todo lo que sabemos sobre sistemas lineales, podemos determinar los valores propios y los vectores propios para obtener las soluciones generales, podemos también determinar la traza, el determinante, el discriminante y determinar la estabilidad de los puntos de equilibrio, etcétera.

Lo que estamos obteniendo es una descripción local del comportamiento de las soluciones del sistema no lineal alrededor de los puntos de equilibrio.

Una aclaración importante es que los planos fase de los sistemas lineales obtenidos están siendo graficados en el plano $UV$, es por ello que cada uno se encuentra centrado en el origen, en el origen de dicho plano.

$\square$

Finalicemos esta entrada con un ejemplo de especies en competencia.

Un modelo de especies en competencia

El sistema Volterra – Lotka es un conocido sistema para especies en competencia y es de la forma

\begin{align*}
x^{\prime} &= x(-Ax -By + C) \\
y^{\prime} &= y(-Dx -Ey + F) \label{17} \tag{17}
\end{align*}

donde $x$ y $y$ son mayores o igual a cero y los parámetros $A -F$ son siempre positivos.

Consideremos un ejemplo particular del sistema Volterra – Lotka. Sean $x$ y $y$ las poblaciones de dos especies que compiten por recursos, un incremento en cualquier especie tiene un efecto adverso sobre la razón de crecimiento de la otra. El modelo es el siguiente.

\begin{align*}
x^{\prime} &= 2x \left( 1 -\dfrac{x}{2} \right) -xy \\
y^{\prime} &= 3y \left( 1 -\dfrac{y}{3} \right) -2xy
\end{align*}

Para un valor dado de $x$, si $y$ se incrementa entonces el término $-xy$ ocasiona que $x^{\prime}$ decrezca. De forma similar, para un valor dado de $y$, si $x$ crece entonces $-2xy$ provoca que $y^{\prime}$ disminuya. Un aumento en la población de cualquiera de las especies ocasiona una disminución en la razón de crecimiento de la otra.

El plano fase del sistema no lineal es

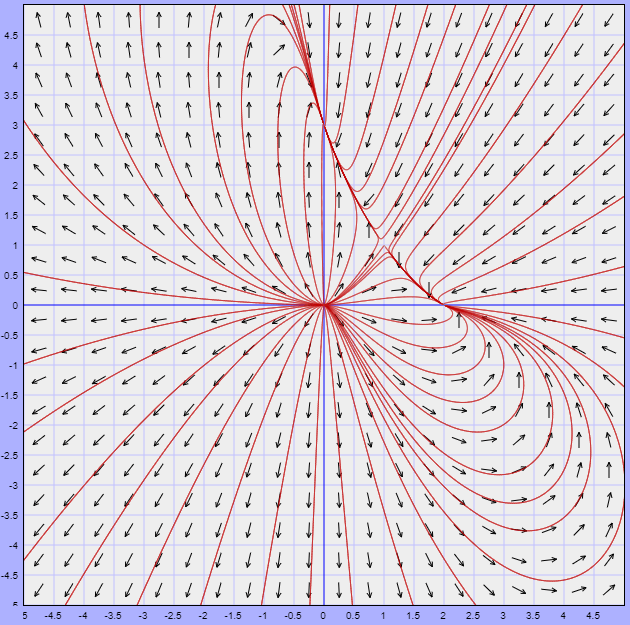
Plano fase del sistema de especies en competencia.

Nota: El plano fase se ilustra para $x$ y $y$ en $\mathbb{R}$, sin embargo, recordemos que el sistema Volterra – Lotka sólo esta definido en el primer cuadrante en el que $x, y \geq 0$, esto debido a que no existen poblaciones negativas. Se puede observar que los cuatro puntos de equilibrio del sistema si pertenecen al primer cuadrante. Sólo consideraremos esta zona.

La funciones $F_{1}(x, y)$ y $F_{2}(x, y)$ son

\begin{align*}
F_{1}(x, y) &= 2x \left( 1 -\dfrac{x}{2} \right) -xy \\
F_{2}(x, y) &= 3y \left( 1 -\dfrac{y}{3} \right) -2xy
\end{align*}

Calculemos las derivadas parciales.

$$\dfrac{\partial F_{1}}{\partial x} = 2 -2x -y, \hspace{1cm} \dfrac{\partial F_{1}}{\partial y} = -x, \hspace{1cm} \dfrac{\partial F_{2}}{\partial x} = -2y, \hspace{1cm} \dfrac{\partial F_{2}}{\partial y} = 3 -2y -2x$$

Por lo tanto, la matriz Jacobiana es

$$\mathbf{J}(x, y) = \begin{pmatrix}
2 -2x -y & -x \\ -2y & 3 -2y -2x
\end{pmatrix}$$

Determinemos los puntos de equilibrio.

\begin{align*}
x(2 -x -y) &= 0 \\
y(3 -y-2x) &= 0
\end{align*}

La primer ecuación se satisface si $x = 0$ o si $2 -x -y = 0$, y la segunda se cumple si $y = 0$ o si $3 -y -2x = 0$.

Supongamos primero que $x = 0$. Entonces la ecuación $y = 0$ da un punto de equilibrio en el origen y $3 -y -2x = 0$ lo proporciona en $(0, 3)$.

Digamos ahora que $2 -x -y = 0$. Entonces la ecuación $y = 0$ da un punto de equilibrio en $(2, 0)$ y $3 -y -2x = 0$ lo da en $(1, 1)$.

Por lo tanto, los puntos de equilibrio son

$$Y_{0} = (0, 0), \hspace{1cm} Y_{1} = (0, 3), \hspace{1cm} Y_{2} = (2, 0) \hspace{1cm} y \hspace{1cm} Y_{3} = (1, 1)$$

Consideremos el punto de equilibrio $Y_{3} = (1,1)$, el cual nos indica que es posible para las dos especies coexistir en equilibrio (como las flores y las abejas que se ayudan a sobrevivir y prosperar mutuamente).

Linealizamos el sistema alrededor del punto de equilibrio $Y_{3} = (1, 1)$, para ello evaluemos en la matriz Jacobiana.

$$\mathbf{J}(1,1) = \begin{pmatrix}
-1 & -1 \\ -2 & -1
\end{pmatrix}$$

Por lo tanto, el sistema lineal que describe al sistema no lineal alrededor del punto de equilibrio $Y_{3} = (1, 1)$, es

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & -1 \\ -2 & -1
\end{pmatrix}\mathbf{Y}$$

Los valores propios del sistema son

$$\lambda_{1} = -1 + \sqrt{2} \hspace{1cm} y \hspace{1cm} \lambda_{2} = -1 -\sqrt{2}$$

como uno es positivo y otro negativo concluimos que el punto de equilibrio es un punto silla. El plano fase del sistema lineal es

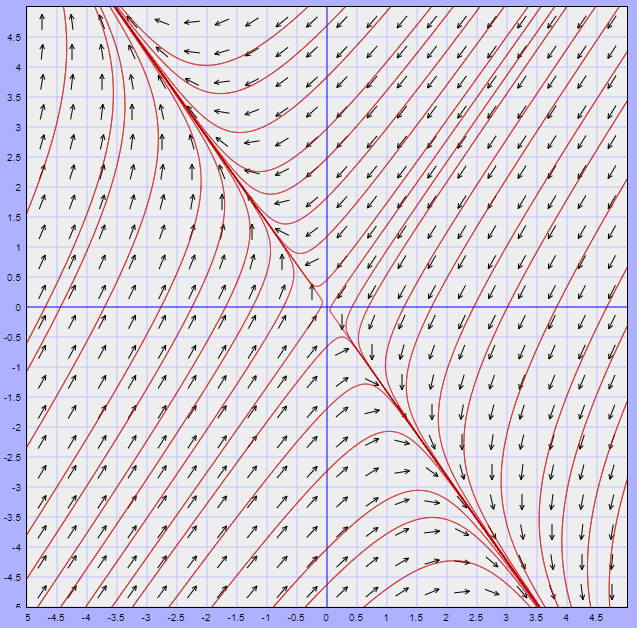
Plano fase linealizado alrededor del punto de equilibrio $Y_{3} = (1, 1)$.

Sólo hay dos trayectorias que tienden hacia el punto de equilibrio $Y_{3} = (1, 1)$ cuando $t$ crece, de modo que bajo cualquier perturbación en las condiciones iniciales provocará que una especie domine sobre la otra, sin embargo, este modelo de especies es muy simplificado que no esperamos ver soluciones que conduzcan al punto de equilibrio $(1, 1)$ en la naturaleza.

De tarea moral linealiza el sistema para el resto de puntos de equilibrio.

$\square$

Ahora sabemos como estudiar las soluciones de un sistema no lineal alrededor de sus puntos de equilibrio, esto sólo nos dará información local, de manera que no es suficiente si lo que queremos es describir las soluciones para tiempos grandes. En la siguiente entrada veremos una técnica que nos permite describir las soluciones lejos de los puntos de equilibrio.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Considerar los siguientes tres sistemas no lineales:

$x^{\prime} = 2x + y$
$y^{\prime} = -y + x^{2}$

$x^{\prime} = 2x + y$
$y^{\prime} = y + x^{2}$

$x^{\prime} = 2x + y$
$y^{\prime} = -y -x^{2}$

Los tres sistemas tienen un punto de equilibrio en $(0,0)$. ¿Cuáles dos sistemas tienen planos fase similares cerca de $(0,0)$?. Justificar la respuesta.

Considerar los siguientes tres sistemas no lineales:

$x^{\prime} = 3 \sin(x) + y$
$y^{\prime} = 4x + \cos(y) -1$

$x^{\prime} = -3 \sin(x) + y$
$y^{\prime} = 4x + \cos(y) -1$

$x^{\prime} = -3 \sin(x) + y$
$y^{\prime} = 4x + 3 \cos(y) -3$

Los tres sistemas tienen un punto de equilibrio en $(0,0)$. ¿Cuáles son los dos sistemas que tienen planos fase similares cerca de $(0,0)$?. Justificar la respuesta.

Dado el siguiente sistema no lineal:

$x^{\prime} = -2x + y$
$y^{\prime} = -y + x^{2}$

Encontrar el sistema linealizado para el punto de equilibrio $(0, 0)$.
Clasificar el punto de equilibrio.
Esbozar el plano fase para el sistema no lineal cerca del origen $(0, 0)$.
Repetir los puntos anteriores para el punto de equilibrio $(2, 4)$.

Para el modelo de población de especies en competencia

$x^{\prime} = 2x \left( 1 -\dfrac{x}{2} \right) -xy$
$y^{\prime} = 3y \left( 1 -\dfrac{y}{3} \right) -2xy$

mostramos que el punto de equilibrio $(1, 1)$ es un punto silla.

Encontrar el sistema linealizado cerca de cada uno de los otros puntos de equilibrio.
Clasificar cada punto de equilibrio.
Esbozar el plano fase de cada sistema linealizado.
Dar una breve descripción del plano fase cerca de cada punto de equilibrio del sistema no lineal.

Considerar el siguiente sistema no lineal:

$x^{\prime} = y -(x^{2} + y^{2})x$
$y^{\prime} = -x-(x^{2} + y^{2})y$

Visualizar el plano fase del sistema.
Determinar los puntos de equilibrio.
Linealizar el sistema con respecto al punto de equilibrio $(0, 0)$.
Visualizar el plano fase del sistema linealizado.

¿Los planos fase de ambos sistemas alrededor del punto de equilibrio $(0, 0)$ son similares?.
¿Qué puede estar sucediendo?.

Más adelante…

Una propiedad interesante del campo vectorial

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y))$$

es que en un punto el vector $F$ puede ser totalmente vertical si la componente $F_{1}$ es cero, o bien puede ser totalmente horizontal se la componente $F_{2}$ es cero. Esta propiedad resultará sumamente útil a la hora de estudiar las trayectorias de un sistema no lineal lejos de un punto de equilibrio.

Al conjunto de puntos en los que alguna de las componentes de la función vectorial $F$ es cero se les denomina nulclinas.

Entradas relacionadas

Página principal del curso: Ecuaciones Diferenciales I
Entrada anterior del curso: El plano Traza – Determinante
Siguiente entrada del curso: Las nulclinas en el estudio cualitativo de los sistemas no lineales

Video relacionado al tema: Sistemas de ecuaciones no lineales. Linealización de puntos de equilibrio

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I: Valores y vectores propios para resolver sistemas lineales

Por Omar González Franco

Deja un comentario

En la vida real, te lo aseguro, no hay algo como el álgebra.
– Fran Lebowitz

Introducción

Ya hemos dado inicio con el desarrollo de métodos de resolución de sistemas lineales de primer orden. En la entrada anterior desarrollamos el método de eliminación de variables que, a pesar de ser muy limitado, es un método sencillo y práctico para resolver sistemas con dos ecuaciones diferenciales lineales de primer orden.

Debido a que un sistema lineal puede ser visto como una ecuación matricial los resultados de álgebra lineal sobre valores y vectores propios de matrices pueden ser aplicados aquí. En esta entrada daremos un breve repaso sobre estos conceptos y veremos cómo es que estos resultados nos pueden ayudar a determinar la solución general de algunos sistemas de ecuaciones diferenciales.

La teoría que desarrollaremos a continuación es aplicable a sistemas lineales homogéneos con coeficientes constantes.

Sistemas lineales homogéneos

Un sistema lineal homogéneo con coeficientes constantes es de la forma

\begin{align*}
y_{1}^{\prime}(t) &= a_{11}y_{1} + a_{12}y_{2} + \cdots + a_{1n}y_{n} \\
y_{2}^{\prime}(t) &= a_{21}y_{1} + a_{22}y_{2} + \cdots + a_{2n}y_{n} \\
&\vdots \\
y_{n}^{\prime}(t) &= a_{n1}y_{1} + a_{n2}y_{2} + \cdots + a_{nn}y_{n} \label{1} \tag{1}
\end{align*}

Si $\mathbf{A}$ es la matriz de $n \times n$ con componentes constantes

$$\mathbf{A} = \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix} \label{2} \tag{2}$$

entonces el sistema lineal a resolver es

$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{3} \tag{3}$$

En la segunda entrada de esta unidad vimos que la solución general del sistema lineal homogéneo

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 3
\end{pmatrix} \mathbf{Y}$$

$$\mathbf{Y}(t) = c_{1} \begin{pmatrix}
1 \\ -1 \\ 0
\end{pmatrix}e^{0t} + c_{2} \begin{pmatrix}
1 \\ 1 \\ 0
\end{pmatrix}e^{2t} + c_{3} \begin{pmatrix}
0 \\ 0 \\ 1
\end{pmatrix}e^{3t}$$

Y en la entrada anterior vimos que la solución del sistema lineal homogéneo

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
4 & -1 \\ 2 & 1
\end{pmatrix} \mathbf{Y}$$

$$\mathbf{Y}(t) = c_{1} \begin{pmatrix}
1 \\ 2
\end{pmatrix} e^{2t} + c_{2} \begin{pmatrix}
1 \\ 1
\end{pmatrix}e^{3t}$$

Aunque para el primer caso aún no sabemos cómo obtener esa solución lo que sabemos es que efectivamente corresponde a la solución general del sistema homogéneo. Notemos que cada vector solución es de la forma

$$\mathbf{Y}_{i} = \begin{pmatrix}
k_{1} \\ k_{2} \\ k_{3}
\end{pmatrix}e^{\lambda_{i}t}, \hspace{1cm} i = 1, 2 ,3$$

donde $k_{i}$ y $\lambda_{i}$, $i = 1, 2, 3$, son constantes. Lo mismo para el segundo caso, con $k_{i}$, $\lambda_{i}$, $i = 1, 2$, constantes. Esta particularidad nos hace preguntarnos si siempre es posible hallar una solución de la forma

$$\mathbf{Y}(t) = \begin{pmatrix}
k_{1} \\ k_{2} \\ \vdots \\ k_{n}
\end{pmatrix}e^{\lambda t} = \mathbf{K}e^{\lambda t} \label{4} \tag{4}$$

como solución general del sistema lineal (\ref{3}).

La respuesta es que sí, pero antes de continuar con nuestro desarrollo nos parece pertinente repasar brevemente algunos conceptos de Álgebra Lineal, en particular el de valores y vectores propios.

Valores y vectores propios

Sea $T: V \rightarrow W$ una transformación lineal, en álgebra lineal muchas veces resulta útil encontrar un vector $v$ en el espacio vectorial $V$ tal que $T\mathbf{v}$ y $\mathbf{v}$ sean paralelos, es decir, se busca un vector $\mathbf{v}$ y un escalar $\lambda$, tal que

$$T\mathbf{v} = \lambda \mathbf{v} \label{5} \tag{5}$$

Recordemos que si $\mathbf{v} \neq \mathbf{0}$ y $\lambda$ satisfacen la ecuación (\ref{5}), entonces $\lambda$ se denomina un valor característico o valor propio de $T$ y $\mathbf{v}$ un vector característico o vector propio de $T$ correspondiente al valor propio $\lambda$.

También recordemos que si $V$ tiene dimensión finita, entonces la transformación $T$ se puede representar por una matriz $\mathbf{A}_{T}$, de manera que se pueden definir los valores y vectores propios de esta matriz.

Denotaremos con $M_{n \times n}$ al conjunto de todas las matrices cuadradas de $n \times n$ con componentes reales y constantes.

Definición: Sea $A \in M_{n \times n}$. El número $\lambda$ (real o complejo) se denomina valor propio de $A$ si existe un vector diferente de cero $\mathbf{v}$ en $V$, tal que
$$\mathbf{Av} = \lambda \mathbf{v} \label{6} \tag{6}$$ El vector $\mathbf{v} \neq \mathbf{0}$ se denomina vector propio de $\mathbf{A}$ correspondiente al valor propio $\lambda$.

Como nota interesante, los valores y vectores propios también son conocidos como valores y vectores característicos o eigenvalores y eigenvectores, donde el término eigen es un término alemán que significa propio. En este curso los llamaremos valores y vectores propios.

Recordemos nuevamente el concepto de matriz inversa.

Definición: Sean $\mathbf{A}$ y $\mathbf{B}$ dos matrices de $M_{n \times n}$. Suponiendo que
$$\mathbf{AB} = \mathbf{BA} = \mathbf{I}$$ Con $\mathbf{I}$ la matriz identidad. Entonces $\mathbf{B}$ se llama la matriz inversa de $\mathbf{A}$ y se denota por $\mathbf{A}^{-1}$.
$$\mathbf{AA}^{-1} = \mathbf{A}^{-1} \mathbf{A} = \mathbf{I} \label{7} \tag{7}$$

Definición: Si $\mathbf{A}$ tiene inversa, entonces se dice que $\mathbf{A}$ es invertible.

Definición: Una matriz cuadrada que no es invertible se le denomina singular y una matriz invertible se llama no singular.

Para el caso especial $\mathbf{A} = \mathbf{I}$, con $\mathbf{I}$ la matriz identidad, se tiene que para cualquier vector $\mathbf{v} \in V$

$$\mathbf{Av} = \mathbf{Iv} = \mathbf{v} \label{8} \tag{8}$$

Así, el único valor propio de $\mathbf{A}$ es $1$ y todo $\mathbf{v} \neq \mathbf{0} \in V$ es un vector propio de $\mathbf{I}$.

Otra observación interesante es que cualquier múltiplo de un vector propio de $\mathbf{A}$ es también un vector propio de $\mathbf{A}$, con el mismo valor propio.

$$\mathbf{A}(c \mathbf{v}) = c \mathbf{Av} = c \lambda \mathbf{v} = \lambda (c \mathbf{v}) \label{9} \tag{9}$$

Ecuación característica

Supongamos que $\lambda $ es un valor propio de $A$, entonces existe un vector diferente de cero

$$\mathbf{v} = \begin{pmatrix}
v_{1} \\ v_{2} \\ \vdots \\ v_{n}
\end{pmatrix} \neq \mathbf{0}$$

tal que

$$\mathbf{Av} = \lambda \mathbf{v} = \lambda \mathbf{Iv} \label{10} \tag{10}$$

Reescribiendo esto, se tiene

$$(\mathbf{A} -\lambda \mathbf{I}) \mathbf{v} = \mathbf{0} \label{11} \tag{11}$$

Si $A$ es una matriz de $n \times n$, la ecuación anterior corresponde a un sistema homogéneo de $n$ ecuaciones con las incógnitas $v_{1}, v_{2}, \cdots, v_{n}$. Como se ha supuesto que $ \mathbf{v} \neq \mathbf{0}$, entonces el sistema no tiene solución trivial y por tanto el determinante de (\ref{11}) debe ser cero.

$$|\mathbf{A} -\lambda \mathbf{I}| = 0 \label{12} \tag{12}$$

De manera equivalente, si ocurre que $|\mathbf{A} -\lambda \mathbf{I}| \neq 0$, entonces la única solución a (\ref{11}) es la trivial $\mathbf{v} = \mathbf{0}$, lo que significa que $\lambda$ no es un valor propio de $A$.

Estos resultados quedan establecidos en el siguiente teorema.

Teorema: Sea $A \in M_{n \times n}$, entonces $\lambda$ es un valor propio de $A$ si y sólo si
$$P(\lambda) = |\mathbf{A} -\lambda \mathbf{I}| = 0 \label{13} \tag{13}$$

La relación (\ref{13}) es muy importante, tanto que merece nombres particulares.

Definición: La relación (\ref{13}) se denomina ecuación característica de $\mathbf{A}$

Definición: El polinomio $P(\lambda)$ dado por (\ref{13}) se denomina polinomio característico de $\mathbf{A}$.

El polinomio $P(\lambda )$ es del mismo grado que el número de filas y columnas de la matriz $\mathbf{A}$. Si $\mathbf{A} \in M_{n \times n}$, entonces $P(\lambda)$ es un polinomio de grado $n$ en $\lambda$. Por ejemplo, si

$$\mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \label{14} \tag{14}$$

entonces,

$$\mathbf{A} -\lambda \mathbf{I} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} -\begin{pmatrix}
\lambda & 0 \\ 0 & \lambda
\end{pmatrix} = \begin{pmatrix}
a -\lambda & b \\ c & d -\lambda
\end{pmatrix} \label{15} \tag{15}$$

\begin{align*}
P(\lambda ) &= |\mathbf{A} -\lambda \mathbf{I}| \\
&= (a -\lambda)(d -\lambda) -bc \\
&= \lambda^{2} -(a + d) \lambda + (ad -bc) \label{16} \tag{16}
\end{align*}

La matriz es de $2 \times 2$ y el polinomio característico es un polinomio de grado $2$.

El teorema fundamental del álgebra nos dice que cualquier polinomio de grado $n$ con coeficientes reales o complejos tiene exactamente $n$ raíces contando multiplicidades y dado que cualquier valor propio de $\mathbf{A}$ es una raíz de la ecuación característica de $\mathbf{A}$, se concluye que, contando multiplicidades, toda matriz $\mathbf{A} \in M_{n \times n}$ tiene exactamente $n$ valores propios.

Realicemos dos ejemplos sencillos en donde determinemos los valores y vectores propios de una matriz. Uno en donde los valores propios sean distintos (con multiplicidad $1$) y uno en donde los valores propios sean números complejos.

Ejemplo: Determinar los valores y vectores propios de la siguiente matriz.

$$\mathbf{A} = \begin{pmatrix}
-81 & 16 \\ -420 & 83
\end{pmatrix}$$

Solución: De acuerdo a (\ref{13}), determinemos la ecuación característica.

$$\begin{vmatrix}
-81 -\lambda & 16 \\ -420 & 83 -\lambda
\end{vmatrix} = (-81 -\lambda)(83 -\lambda) -16(-420) = 0$$

Reordenando obtenemos que la ecuación característica es

$$\lambda^{2} -2 \lambda -3 = 0$$

y el polinomio característico es

$$P(\lambda) = \lambda^{2} -2 \lambda -3$$

Resolviendo para $\lambda$ se obtienen las raíces $\lambda_{1} = -1$ y $\lambda_{2} = 3$. Para obtener los vectores propios buscamos un vector $\mathbf{v} \neq 0$, tal que se cumpla (\ref{11}) para cada valor propio $\lambda$. Comencemos con $\lambda_{1}$.

Caso 1: $\lambda_{1} = -1$.

$$\begin{pmatrix}
-81 -(-1) & 16 \\ -420 & 83 -(-1)
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
-80 & 16 \\ -420 & 84
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

Este resultado lo podemos escribir como las siguientes dos ecuaciones.

\begin{align*}
-80 v_{1} + 16 v_{2} &= 0 \\
-420 v_{1} + 84 v_{2} &= 0
\end{align*}

Que en realidad corresponden a una sola.

\begin{align*}
-5v_{1} + v_{2} &= 0 \\
v_{2} &= 5v_{1}
\end{align*}

Si elegimos $v_{1} = 1$, entonces $v_{2} = 5$, así el primer vector propio es

$$\mathbf{v}_{1} = \begin{pmatrix}
1 \\ 5
\end{pmatrix}$$

Caso 2: $\lambda_{2} = 3$.

$$\begin{pmatrix}
-81 -3 & 16 \\ -420 & 83-3
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
-84 & 16 \\ -420 & 80
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

La ecuación que se obtiene es

\begin{align*}
-21v_{1} + 4v_{2} &= 0 \\
v_{2} &= \dfrac{21}{4}v_{1}
\end{align*}

Por conveniencia elegimos $v_{1} = 4$, entonces $v_{2} = 21$, así

$$\mathbf{v}_{2} = \begin{pmatrix}
4 \\ 21
\end{pmatrix}$$

En conclusión, los valores y vectores propios de la matriz $\mathbf{A}$ son $\lambda_{1} = -1$, $\lambda_{2} = 3$, $\mathbf{v}_{1} = \begin{pmatrix} 1 \\ 5 \end{pmatrix}$ y $\mathbf{v}_{2} = \begin{pmatrix} 4 \\ 21 \end{pmatrix}$, respectivamente.

$\square$

Realicemos el segundo ejemplo.

Ejemplo: Determinar los valores y vectores propios de la siguiente matriz.

$$\mathbf{A} = \begin{pmatrix}
2 & -1 \\ 5 & -2
\end{pmatrix}$$

Solución: Determinemos la ecuación característica.

$$\begin{vmatrix}
2 -\lambda & -1 \\ 5 & -2 -\lambda
\end{vmatrix} = (2 -\lambda)(-2 -\lambda) + 5 = 0$$

La ecuación característica es

$$\lambda^{2} + 1 = 0$$

De donde $\lambda_{1} = i$ y $\lambda_{2} = -i$. Determinemos los vectores propios.

Caso 1: $\lambda_{1} = i$.

$$\begin{pmatrix}
2 -i & -1 \\ 5 & -2 -i
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

Las ecuaciones que se obtienen son

\begin{align*}
(2 -i)v_{1} -v_{2} &= 0 \\
5v_{1} -(2 + i)v_{2} &= 0
\end{align*}

Resolviendo el sistema se obtiene que $v_{1} = 2 + i$ y $v_{2} = 5$, así

$$\mathbf{v}_{1} = \begin{pmatrix}
2 + i \\ 5
\end{pmatrix}$$

Caso 2: $\lambda_{2} = -i$

$$\begin{pmatrix}
2 + i & -1 \\ 5 & -2 + i
\end{pmatrix} \begin{pmatrix}
v_{1} \\ v_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

Las ecuaciones que se obtienen son

\begin{align*}
(2 + i) v_{1} -v_{2} &= 0 \\
5v_{1} + (-2 + i)v_{2} &= 0
\end{align*}

Resolviendo el sistema se obtiene que $v_{1} = 2 -i$ y $v_{2} = 5$, así

$$\mathbf{v}_{2} = \begin{pmatrix}
2 -i \\ 5
\end{pmatrix}$$

$\square$

En caso de requerir conocer más a fondo sobre el algoritmo que llevamos a cabo para obtener los valores y vectores propios de una matriz se recomienda revisar directamente en el curso de Álgebra Lineal I. Recordemos que aquí sólo estamos haciendo un breve repaso.

Para concluir con nuestro repaso, enunciemos un teorema de suma importancia que nos será de utilidad mas adelante. Haremos la demostración por inducción.

Teorema: Sea $\mathbf{A} \in M_{n \times n}$ y sean $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{m}$ valores propios distintos de $\mathbf{A}$ ($\lambda_{i} \neq \lambda_{j}$, $i \neq j$) con vectores propios correspondientes $\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{m}$, entonces los vectores $\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{m}$ son linealmente independientes.

Demostración: Como el caso $m = 1$ se trata de un solo vector es evidente que se satisface el teorema, hagamos el caso $m = 2$, para ello consideremos la combinación lineal

$$c_{1} \mathbf{v}_{1} + c_{2} \mathbf{v}_{2} = \mathbf{0} \label{17} \tag{17}$$

Multipliquemos ambos lados de la ecuación por la matriz $\mathbf{A}$.

$$c_{1} \mathbf{Av}_{1} + c_{2} \mathbf{Av}_{2} = \mathbf{0} \label{18} \tag{18}$$

Como $\mathbf{Av}_{i} = \lambda_{i}\mathbf{v}_{i}$, para $i = 1, 2$, entonces

$$c_{1} \lambda_{1} \mathbf{v}_{1} + c_{2} \lambda_{2} \mathbf{v}_{2} = \mathbf{0} \label{19} \tag{19}$$

A la ecuación (\ref{17}) la multiplicamos por $\lambda_{1}$ y la restamos de la ecuación (\ref{19}).

$$(c_{1} \lambda_{1} \mathbf{v}_{1} + c_{2} \lambda_{2} \mathbf{v}_{2}) -(c_{1} \lambda_{1} \mathbf{v}_{1} -c_{2} \lambda_{1} \mathbf{v}_{2}) = \mathbf{0}$$

que se reduce a

$$c_{2}(\lambda_{2} -\lambda_{1}) \mathbf{v}_{2} = \mathbf{0} \label{20} \tag{20}$$

Como $\mathbf{v}_{2} \neq \mathbf{0}$ por definición de vector característico y por hipótesis $\lambda_{1} \neq \lambda_{2}$, entonces se concluye que $c_{2} = 0$, sustituyendo en (\ref{17}) se ve que $c_{1} = 0$, por tanto se cumple el teorema para $m = 2$, es decir, $\mathbf{v}_{1}$ y $\mathbf{v}_{2}$ son linealmente independientes.

Ahora supongamos que el teorema es cierto para $m = n$, es decir, cualquier conjunto de $n$ vectores propios de $\mathbf{A}$ con valores propios diferentes es linealmente independiente. Hay que demostrar que cualquier conjunto de $n + 1$ vectores propios de $\mathbf{A}$ con valores propios diferentes es también linealmente independiente. La demostración sigue el mismo procedimiento que como lo hicimos para $m = 2$, consideremos la siguiente combinación lineal.

$$c_{1} \mathbf{v}_{1} + c_{2} \mathbf{v}_{2} + \cdots + c_{n + 1} \mathbf{v}_{n + 1} = \mathbf{0} \label{21} \tag{21}$$

Multipliquemos por $\mathbf{A}$ en ambos lados.

$$c_{1} \mathbf{Av}_{1} + c_{2} \mathbf{Av}_{2} + \cdots + c_{n + 1} \mathbf{Av}_{n + 1} = \mathbf{0} \label{22} \tag{22}$$

Aplicando $\mathbf{Av}_{i} = \lambda_{i} \mathbf{v}_{1}$ para $i = 1, 2, 3, \cdots, n + 1$, se tiene

$$c_{1} \lambda_{1} \mathbf{v}_{1} + c_{2} \lambda_{2} \mathbf{v}_{2} + \cdots + c_{n + 1} \lambda_{n + 1} \mathbf{v}_{n + 1} = \mathbf{0} \label{23} \tag{23}$$

Si se multiplica ambos lados de la ecuación (\ref{21}) por $\lambda_{1}$ y se resta de (\ref{23}), se obtiene

$$c_{2}(\lambda_{2} -\lambda_{1}) \mathbf{v}_{2} + c_{3}(\lambda_{3} -\lambda_{1}) \mathbf{v}_{3} + \cdots + c_{n + 1}(\lambda_{n + 1} -\lambda_{1})\mathbf{v}_{n + 1} = \mathbf{0} \label{24} \tag{24}$$

Pero $\mathbf{v}_{2}, \mathbf{v}_{3}, \cdots, \mathbf{v}_{n + 1}$ son vectores propios de $\mathbf{A}$ con valores propios distintos $\lambda_{2}, \lambda_{3}, \cdots, \lambda_{n + 1}$, respectivamente. Por hipótesis de inducción, los vectores son linealmente independientes, así que

$$c_{2}(\lambda_{2} -\lambda_{1}) = 0, \hspace{1cm} c_{3}(\lambda_{3} -\lambda_{1}) = 0, \hspace{1cm} \cdots, \hspace{1cm} c_{n + 1}(\lambda_{n + 1} -\lambda_{1}) = 0$$

Como los valores propios son distintos entre sí, entonces necesariamente

$$c_{2} = c_{3} = \cdots = c_{n + 1} = 0$$

Con este resultado la ecuación (\ref{21}) obliga a que $c_{1}$ sea cero. Por lo tanto, $\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}, \cdots, \mathbf{v}_{n + 1}$ son linealmente independientes. De esta manera queda demostrado el teorema.

$\square$

En conclusión, vectores propios correspondientes a valores propios distintos son linealmente independientes.

Con este breve repaso en mente regresemos a los sistemas de ecuaciones diferenciales.

Valores y vectores propios en sistemas de ecuaciones diferenciales

Ahora que hemos recordado las definiciones de valores y vectores propios y algunas propiedades veamos cómo es que estos conceptos son útiles para resolver sistemas lineales de primer orden homogéneos.

Al inicio de la entrada decíamos que es posible encontrar soluciones de la forma (\ref{4}).

$$\mathbf{Y}(t) = \begin{pmatrix}
k_{1} \\ k_{2} \\ \vdots \\ k_{n}
\end{pmatrix}e^{\lambda t} = \mathbf{K}e^{\lambda t}$$

Si derivamos este vector, se obtiene

$$\mathbf{Y}^{\prime} = \mathbf{K} \lambda e^{\lambda t} \label{25} \tag{25}$$

Sustituyamos en el sistema homogéneo $\mathbf{Y}^{\prime} = \mathbf{AY}$.

$$\mathbf{K} \lambda e^{\lambda t} = \mathbf{AK}e^{\lambda t} \label{26} \tag{26}$$

Si dividimos entre $e^{\lambda t}$ y reordenamos, se tiene

$$\mathbf{AK} = \lambda \mathbf{K}$$

o bien,

$$\mathbf{AK} -\lambda \mathbf{K} = \mathbf{0}$$

Debido a que $\mathbf{K} = \mathbf{IK}$, con $\mathbf{I}$ la matriz identidad, la última expresión se puede escribir como

$$(\mathbf{A} -\lambda \mathbf{I}) \mathbf{K} = \mathbf{0}\label{27} \tag{27}$$

Si $\mathbf{A}$ es la matriz dada en (\ref{2}), entonces la ecuación matricial (\ref{27}) es equivalente a las $n$ ecuaciones algebraicas simultáneas

\begin{align*}
(a_{11} -\lambda)k_{1} + \hspace{1.2cm} a_{12}k_{2} + \cdots + \hspace{1.2cm} a_{1n}k_{n} &= 0 \\
a_{21}k_{1} + (a_{22} -\lambda)k_{2} + \cdots + \hspace{1.2cm} a_{2n}k_{n} &= 0 \\
\vdots \\
a_{n1}k_{1} + \hspace{1.2cm} a_{n2}k_{2} + \cdots + (a_{nn} -\lambda)k_{n} &= 0 \label{28} \tag{28}
\end{align*}

Si queremos encontrar soluciones $\mathbf{Y}(t)$ como (\ref{4}), necesitamos primero encontrar una solución no trivial del sistema (\ref{28}), de lo visto en nuestro repaso de valores y vectores propios, si la solución debe ser la no trivial, entonces se requiere que el determinante sea igual a cero, esto es

$$|\mathbf{A} -\lambda \mathbf{I}| = 0 \label{29} \tag{29}$$

Esta ecuación polinomial corresponde a la ecuación característica de la matriz $\mathbf{A}$. Sus soluciones son los valores propios de $\mathbf{A}$. Una solución $\mathbf{K} \neq 0$ de (\ref{27}) correspondiente a un valor propio $\lambda$ es el vector propio de $\mathbf{A}$.

La ecuación (\ref{29}) al tratarse de una ecuación polinomial existen tres casos posibles, cuando los valores propios son reales y distintos, cuando son repetidos y cuando son complejos. Para cada caso existe una forma particular de la solución de (\ref{3}).

Para concluir con esta entrada demostremos un resultado que establece la forma de la solución general del sistema lineal (\ref{3}).

Teorema: Sea $\mathbf{A} \in M_{n \times n}$ como (\ref{2}) y sean $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ valores propios de $\mathbf{A}$ que corresponden a vectores propios linealmente independientes $\mathbf{K}_{1}, \mathbf{K}_{2}, \cdots, \mathbf{K}_{n}$, respectivamente. Entonces,
$$S = \{e^{\lambda_{1}t} \mathbf{K}_{1}, e^{\lambda_{2}t} \mathbf{K}_{2}, \cdots, e^{\lambda_{n}t} \mathbf{K}_{n}\} \label{30} \tag{30}$$ es un conjunto fundamental de soluciones del sistema lineal homogéneo $\mathbf{Y}^{\prime} = \mathbf{AY}$ en el intervalo $(-\infty, \infty)$. La solución general de dicho sistema es
$$\mathbf{Y}(t) = c_{1} e^{\lambda_{1}t} \mathbf{K}_{1} + c_{2} e^{\lambda_{2}t} \mathbf{K}_{2} + \cdots + c_{n} e^{\lambda_{n}t} \mathbf{K}_{n} \label{31} \tag{31}$$ donde $c_{1}, c_{2}, \cdots, c_{n}$ son constantes arbitrarias.

Demostración: Definamos las funciones

$$\mathbf{Y}_{1}(t) = e^{\lambda_{1}t}\mathbf{K}_{1}, \hspace{1cm} \mathbf{Y}_{2}(t) = e^{\lambda_{2}t}\mathbf{K}_{2}, \hspace{1cm} \cdots, \hspace{1cm} \mathbf{Y}_{n}(t) = e^{\lambda_{n}t} \mathbf{K}_{n}$$

Notemos que para la $i$-ésima función $\mathbf{Y}_{i}(t) = e^{\lambda_{i}t} \mathbf{K}_{i}$ se cumple lo siguiente.

$$\mathbf{Y}^{\prime}_{i} = e^{\lambda_{i}t} (\lambda_{i} \mathbf{K}_{i}) = e^{\lambda_{i}t} (\mathbf{AK}_{i}) = \mathbf{AY}_{i} \label{32} \tag{32}$$

En donde se hecho uso de la relación (\ref{6}). Esto nos muestra que $\mathbf{Y}_{i}(t)$ es solución del sistema $\mathbf{Y}^{\prime} = \mathbf{AY}$ para cada $i = 1, 2, \cdots, n$. Basta mostrar que el Wronskiano es distinto de cero para probar que las funciones definidas forman un conjunto fundamental de soluciones. El Wronskiano está dado por

\begin{align*}
W(\mathbf{Y}_{1}, \mathbf{Y}_{2}, \cdots,\mathbf{Y}_{n}) &= \begin{vmatrix} e^{\lambda_{1}t} \mathbf{K}_{1} & e^{\lambda_{2}t} \mathbf{K}_{2} & \cdots & e^{\lambda_{n}t} \mathbf{K}_{n} \end{vmatrix} \\
&= e^{(\lambda_{1} + \lambda_{2} + \cdots + \lambda_{n})t} \begin{vmatrix} \mathbf{K}_{1} & \mathbf{K}_{2} & \cdots & \mathbf{K}_{n} \end{vmatrix} \label{33} \tag{33}
\end{align*}

Como la exponencial nunca se hace cero y por hipótesis los vectores $\mathbf{K}_{1}, \mathbf{K}_{2}, \cdots, \mathbf{K}_{n}$ son linealmente independientes, es decir, el determinante nunca es cero

$$\begin{vmatrix} \mathbf{K}_{1} & \mathbf{K}_{2} & \cdots & \mathbf{K}_{n} \end{vmatrix} \neq 0 \label{34} \tag{34}$$

entonces el Wronskiano es distinto de cero. Por el teorema de solución general de un sistema homogéneo concluimos que el conjunto

$$S = \{e^{\lambda_{1}t} \mathbf{K}_{1}, e^{\lambda_{2}t} \mathbf{K}_{2}, \cdots, e^{\lambda_{n}t} \mathbf{K}_{n}\}$$

es un conjunto fundamental de soluciones del sistema $\mathbf{Y}^{\prime} = \mathbf{AY}$ y la solución general es

$$\mathbf{Y}(t) = c_{1} e^{\lambda_{1}t} \mathbf{K}_{1} + c_{2} e^{\lambda_{2}t} \mathbf{K}_{2} + \cdots + c_{n} e^{\lambda_{n}t} \mathbf{K}_{n}$$

con $c_{1}, c_{2}, \cdots, c_{n}$ constantes arbitrarias.

$\square$

En la siguiente entrada aplicaremos todo esto en el desarrollo de un nuevo método de resolución de sistemas lineales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Obtener los valores y vectores propios de las siguientes matrices.

$\mathbf{A} = \begin{pmatrix}
-62 & -20 \\ 192 & 62
\end{pmatrix}$

$\mathbf{A} = \begin{pmatrix}
-2 & 5 & 0 \\ 5 & -2 & 0 \\ 0 & 0 & 1
\end{pmatrix}$

Demostrar que para cualesquiera números reales $\alpha$ y $\beta$, la matriz $$\mathbf{A} = \begin{pmatrix} \alpha & \beta \\ -\beta & \alpha \end{pmatrix}$$ tiene valores propios $\alpha \pm i\beta$.

Suponer que la matriz $\mathbf{A}$ tiene valores propios $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$. Demostrar lo siguiente:

Demostrar que $\mathbf{A}^{-1}$ (la matriz inversa de $\mathbf{A}$) existe si y sólo si $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$ son todos distintos de cero.

Si $\mathbf{A}^{-1}$ existe, demostrar que los valores propios de $\mathbf{A}^{-1}$ son $\dfrac{1}{\lambda_{1}}, \dfrac{1}{\lambda_{2}}, \cdots, \dfrac{1}{\lambda_{n}}$.

Suponer que la matriz $\mathbf{A}$ tiene valores propios $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$. Demostrar que la matriz $\mathbf{A} -\alpha \mathbf{I}$ tiene valores propios $\lambda_{1} -\alpha, \lambda_{2} -\alpha, \cdots, \lambda_{n} -\alpha$.

Suponer que la matriz $\mathbf{A}$ tiene valores propios $\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}$. Demostrar que los valores propios de $\mathbf{A}^{m}$ son $\lambda^{m}_{1}, \lambda^{m}_{2}, \cdots, \lambda^{m}_{n}$ para $m = 1, 2, 3, \cdots$.

Recuerda que para calcular la potencia de una matriz, debemos multiplicar la matriz por ella misma tantas veces como indique el exponente, por ejemplo
$$\mathbf{A}^{5} = \mathbf{A} \cdot \mathbf{A} \cdot \mathbf{A} \cdot \mathbf{A} \cdot \mathbf{A}$$

Más adelante…

Un nuevo método para resolver sistemas de ecuaciones diferenciales lineales de primer orden homogéneas con coeficientes constantes es el que estamos por desarrollar. Dicho método involucra obtener los valores y vectores propios de la matriz que conforma al sistema lineal, es por ello que hemos dedicado esta entrada en hacer un breve repaso sobre estos conceptos y hemos visto cómo es que se ven involucrados en la resolución de estos sistemas.

Como vimos, los valores propios se obtienen de encontrar las raíces del polinomio característico lo que significa que se pueden tener raíces reales y distintas, raíces con multiplicidad mayor a uno, es decir, que se repiten o raíces complejas, para cada caso existe una forma distinta de obtener la solución de los sistemas lineales homogéneos $\mathbf{Y}^{\prime} = \mathbf{AY}$.

En las próximas tres entradas estudiaremos cada caso. Comenzaremos con el caso en el que los valores propios del sistema son todos reales y distintos entre sí.

Entradas relacionadas

Página principal del curso: Ecuaciones Diferenciales I
Entrada anterior del curso: Método de eliminación de variables
Siguiente entrada del curso: Sistemas lineales homogéneos con coeficientes constantes – Valores propios distintos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Propiedades del conjunto de soluciones a un sistema lineal de ecuaciones de primer orden

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos el estudio de los sistemas de ecuaciones diferenciales de primer orden $$\begin{alignedat}{4} \dot{x}_{1} &= F_{1}(t,x_{1},x_{2},…,x_{n}) \\ \dot{x}_{2} &= F_{2}(t,x_{1},x_{2},…,x_{n}) \\ & \; \; \vdots \notag \\ \dot{x}_{n} &= F_{n}(t,x_{1},x_{2},…,x_{n}) \end{alignedat}$$ donde revisamos las principales definiciones y enunciamos el teorema de existencia y unicidad correspondiente a sistemas de primer orden y sus problemas de condición inicial. Es momento ahora de estudiar las principales propiedades que cumple el conjunto de soluciones a un sistema lineal de ecuaciones de primer orden, las cuales se comportan de una manera bastante similar al conjunto de soluciones a una ecuación de segundo orden lineal que revisamos en la unidad anterior.

Iniciaremos revisando al conjunto de soluciones al sistema lineal homogéneo $$\dot{\textbf{X}}={\textbf{A}}{\textbf{X}}$$ el cual cumple el principio de superposición, es decir, si tenemos $n$ soluciones, digamos ${\textbf{X}_{1}}(t), {\textbf{X}_{2}}(t),…,{\textbf{X}_{n}}(t)$, entonces cualquier combinación lineal de estas también lo será. Si recuerdas tus cursos de Álgebra Lineal, esta última propiedad nos dice que el conjunto de soluciones es cerrado bajo la suma y producto por escalar usuales definidos para matrices. Con estas operaciones, veremos que el conjunto de soluciones al sistema lineal homogéneo forma un espacio vectorial.

Posteriormente definiremos el Wronskiano de un subconjunto de soluciones al sistema lineal homogéneo, el cual es similar más no igual al Wronskiano que definimos para ecuaciones lineales de segundo orden. En la tarea moral demostrarás la relación que tienen estos dos Wronskianos.

Si hablamos del Wronskiano y del conjunto de soluciones como un espacio vectorial, debemos hablar también de dependencia e independencia lineal entre las soluciones al sistema. Además, demostraremos que si el Wronskiano no se anula entonces el subconjunto de soluciones es linealmente independiente. Además si lo último ocurre podremos expresar cualquier solución como una combinación lineal de las soluciones linealmente independientes. Con estos conceptos podremos definir a la matriz fundamental de soluciones del sistema, la cual revisaremos más a detalle en entradas posteriores.

Terminaremos revisando el caso no homogéneo $$\dot{\textbf{X}}={\textbf{A}}{\textbf{X}}+ {\textbf{Q}}$$ demostrando que su solución general será la suma de la solución general al sistema homogéneo y una solución particular al sistema no homogéneo.

El espacio vectorial del conjunto de soluciones a un sistema lineal homogéneo

En el primer video probamos el principio de superposición de soluciones al sistema lineal homogéneo. Además, vemos que el conjunto de soluciones al sistema forma un espacio vectorial con la suma y producto por escalar usuales para matrices.

El Wronskiano de un subconjunto de soluciones e independencia lineal

Definimos el Wronskiano de un subconjunto de soluciones al sistema lineal homogéneo, así como los conceptos de dependencia e independencia lineal de soluciones. Probamos un importante teorema que relaciona estos dos conceptos y nos dice cómo se ve la solución general al sistema. Finalizamos definiendo la matriz fundamental de soluciones del sistema.

Solución general al sistema lineal no homogéneo

Finalizamos la entrada demostrando que la solución general al sistema lineal no homogéneo es la suma de la solución general al sistema homogéneo y una solución particular al sistema no homogéneo.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

¿El conjunto de soluciones a un sistema lineal no homogéneo forma un espacio vectorial con las operaciones usuales de matrices?

Prueba que $$\textbf{X}_{1}(t)=\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} ; \, \textbf{X}_{2}(t)=\begin{pmatrix} t \\ 2 \\ 0 \end{pmatrix} ; \, \textbf{X}_{3}(t)=\begin{pmatrix} t^{2} \\ t \\ 0 \end{pmatrix}$$ son linealmente independientes en $\mathbb{R}.$

Sean ${\textbf{X}_{1}}(t), {\textbf{X}_{2}}(t),…,{\textbf{X}_{n}}(t)$ soluciones al sistema $$\dot{\textbf{X}}={\textbf{A}}{\textbf{X}}$$ en el intervalo $[a,b]$. Demuestra que $W[{\textbf{X}_{1}}, {\textbf{X}_{2}},…,{\textbf{X}_{n}}](t)=0 \, \, \forall t \in [a,b]$, ó $W[{\textbf{X}_{1}}, {\textbf{X}_{2}},…,{\textbf{X}_{n}}](t) \neq 0 \, \, \forall t \in [a,b]$.

Considera el sistema lineal $$\dot{\textbf{X}}=\begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} \textbf{X}.$$ Prueba que $$\textbf{X}_{1}(t)=\begin{pmatrix} e^{t} \\ -e^{t} \end{pmatrix} ; \, \textbf{X}_{2}(t)=\begin{pmatrix} e^{-t} \\ e^{-t} \end{pmatrix}$$ son soluciones al sistema. Además prueba que son linealmente independientes en $\mathbb{R}$ y por lo tanto forma una matriz fundamental de soluciones al sistema.

Considera la ecuación $$\ddot{y}+p(t)\dot{y}+q(t)y=0$$ y su sistema de ecuaciones correspondiente $$\dot{\textbf{X}}=\begin{pmatrix} 0 & 1 \\ -q(t) & -p(t) \end{pmatrix} \textbf{X}.$$ Prueba que si $\textbf{X}_{1}(t)$, $\textbf{X}_{2}(t)$ son soluciones linealmente independientes al sistema de ecuaciones, y si $y_{1}(t)$, $y_{2}(t)$ forman un conjunto fundamental de soluciones a la ecuación de segundo orden, entonces se satisface la identidad $$W[y_{1}, y_{2}](t)=cW[\textbf{X}_{1}, \textbf{X}_{2}](t)$$ para alguna constante $c \neq 0$.

Más adelante

En la siguiente entrada comenzaremos a resolver algunos sistemas lineales bastante sencillos. El método que estudiaremos será el de eliminación de variables, el cual consiste en eliminar variables dependientes hasta quedarnos con una ecuación diferencial de orden superior. Resolviendo esta última ecuación podremos encontrar la solución general al sistema original. Este método funciona para sistemas lineales con coeficientes constantes.

¡Hasta la próxima!

Entradas relacionadas

Ir a Ecuaciones Diferenciales I
Entrada anterior del curso: Introducción a sistemas de ecuaciones de primer orden
Siguiente entrada del curso: Método de eliminación de variables

Notas escritas relacionadas con el tema: Soluciones a sistemas de ecuaciones diferenciales

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Sistemas de ecuaciones lineales y sistemas homogéneos asociados

Por Julio Sampietro

2 respuestas

Introducción

En esta sección damos un primer acercamiento al concepto de sistemas de ecuaciones lineales. Este es un concepto de fundamental importancia en muchas áreas de las matemáticas, como las ecuaciones diferenciales o incluso la geometría algebraica.

Los sistemas de ecuaciones lineales nos son familiares. Desde la educación secundaria se aprende a resolver ecuaciones «de $2\times 2$», y más adelante «de $3\times 3$». Estos sistemas también aparecen en cursos de la licenciatura, como geometría analítica. Sin embargo, es en un curso de álgebra lineal que se estudian con toda generalidad. Las herramientas de esta área de las matemáticas permiten determinar si un sistema de ecuaciones lineales tiene solución y, en caso de que sí, ver cómo se ven todas las soluciones.

Como veremos a continuación, un sistema de ecuaciones lineales se puede ver en términos de matrices. Esta conexión es fundamental. La información acerca de una matriz nos permite obtener información acerca del sistema de ecuaciones lineales asociado. A la vez, la información sobre un espacio o matriz se puede determinar a partir de la resolución de sistemas de ecuaciones lineales.

Sistemas de ecuaciones lineales

Una ecuación lineal en variables $x_1, \dots, x_n$ es una ecuación de la forma

\begin{align*}
a_1 x_1 + \dots +a_n x_n =b,
\end{align*}

donde $a_1, \dots, a_n, b\in F$ son escalares dados y $n$ es un entero positivo. Las incógnitas $x_1,\dots, x_n$ suponen ser elementos de $F$.

Un sistema de ecuaciones lineales en las variables $x_1, \dots, x_n$ es una familia de ecuaciones lineales, usualmente escrito como

\begin{align*}
\begin{cases}
a_{11}x_1+a_{12} x_2+\dots +a_{1n} x_n = b_1\\
a_{21} x_1 +a_{22} x_2 + \dots + a_{2n} x_n = b_2\\
\quad \vdots\\
a_{m1} x_1+a_{m2} x_2+\dots + a_{mn}x_n = b_m
\end{cases}.
\end{align*}

Aquí de nuevo los $a_{ij}$ y los $b_i$ son escalares dados. Resolver un sistema de ecuaciones lineales consiste en describir todos los posibles valores que pueden tener $x_1,\ldots,x_n$ de modo que todas las ecuaciones anteriores se satisfagan simultáneamente.

La notación que usamos no es mera coincidencia y nos permite describir de manera mucho más concisa el sistema: Si $X$ es un vector columna con entradas $x_1, \dots, x_n$, $A$ es la matriz en $M_{m,n}(F)$ con entradas $[a_{ij}]$ y $b$ es un vector columna en $F^m$ con entradas $b_1, \dots, b_m$ entonces el sistema se reescribe como

\begin{align*}
AX=b.
\end{align*}

Puedes verificar esto usando la definición de $A$ como transformación lineal y comparando los vectores en ambos lados de la igualdad entrada a entrada. Resolver el sistema se traduce entonces a responder cómo son todos los vectores $X$ en $F^n$ que satisfacen la igualdad anterior.

Ejemplo. A continuación tenemos un sistema de ecuaciones en tres variables (o incógnitas) $x_1$, $x_2$ y $x_3$:

\begin{align*}
\begin{cases}
3x_1-2x_2+7x_3&=5\\
4x_1+3x_3&=7\\
2x_1+x_2-7x_3&=-1\\
-x_1+3x_2&=8
\end{cases}.
\end{align*}

Si tomamos al vector $b=\begin{pmatrix} 5 \\ 7 \\ -1 \\8 \end{pmatrix}$ en $\mathbb{R}^4$, al vector de incógnitas $X=\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ y a la matriz $$A=\begin{pmatrix} 3 & -2 & 7\\ 4 & 0 & 3 \\ 2 & 1 & -7 \\ -1 & 3 & 0\end{pmatrix},$$ entonces el sistema de ecuaciones lineales consiste exactamente en determinar aquellos vectores $X$ en $\mathbb{R}^3$ tales que $$AX=b.$$

$\triangle$

También podríamos describir nuestro sistema en términos solo de vectores. Recordando un resultado visto en la entrada de producto de matrices, si $C_1, \dots, C_n$ son las columnas de $A$, vistos como vectores columna en $F^{m}$, el sistema es equivalente a

\begin{align*}
x_1 C_1+x_2 C_2 +\dots +x_n C_n=b.
\end{align*}

Sistemas de ecuaciones lineales homogéneos

Hay un tipo de sistemas de ecuaciones lineales muy especiales: aquellos en los que $b=0$. Son tan importantes, que tienen un nombre especial.

Definición.

El sistema de ecuaciones lineales $AX=b$ se dice homogéneo si $b=0$ (es decir si $b_1= b_2=\dots= b_m=0$).
Dado un sistema $AX=b$, el sistema lineal homogéneo asociado es el sistema $AX=0$.

Así, un sistema es homogéneo si es de la forma $AX=0$ para alguna matriz $A$.

Ejemplo. Considera el siguiente sistema de ecuaciones lineales:

\begin{align*}
\begin{cases}
2x+3y-z&=-1\\
5x+8z&=0\\
-x+y&=1.
\end{cases}
\end{align*}

Este es un sistema de ecuaciones que en representación matricial se ve así:

\begin{align*}
\begin{pmatrix} 2 & 3 & -1 \\ 5 & 0 & 8 \\ -1 & 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} -1 \\ 0 \\ 1\end{pmatrix}.
\end{align*}

Como el vector en el lado derecho de la igualdad no es el vector cero, entonces este no es un sistema homogéneo. Sin embargo, tiene asociado el siguiente sistema lineal homogéneo:

\begin{align*}
\begin{pmatrix} 2 & 3 & -1 \\ 5 & 0 & 8 \\ -1 & 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix}=
\begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix}.
\end{align*}

$\triangle$

Para la resolución de sistemas lineales en general, el sistema homogéneo asociado juega un papel crucial gracias al siguiente resultado, que nos dice esencialmente que para resolver un sistema $AX=b$ basta con encontrar un vector solución $X_0$ y resolver el sistema homogéneo asociado.

Proposición. (Principio de superposición) Sea $A\in M_{m,n}(F)$ y $b\in F^{m}$. Sea $\mathcal{S}\subset F^{n}$ el conjunto de soluciones del sistema homogéneo asociado $AX=0$. Si el sistema $AX=b$ tiene una solución $X_0$, entonces el conjunto de soluciones del sistema $AX=b$ no es más que

\begin{align*}
X_0+\mathcal{S}= \lbrace X_0 +s\mid s\in \mathcal{S} \rbrace.
\end{align*}

Demostración: Por hipótesis, $AX_0=b$. Ahora al sustituir, $AX=b$ si y sólo si $AX=A X_0$, o bien $A(X-X_0)=0$. Es decir, un vector $X$ es solución de $AX=b$ si y sólo si $X-X_0$ es solución de $AY=0$, de otra manera, si y sólo si $X-X_0\in \mathcal{S}$. Pero esto último es equivalente a decir que existe $s\in \mathcal{S}$ tal que $X-X_0=s$, luego $X= X_0 +s\in X_0 +\mathcal{S}$. Esto prueba el resultado.

$\square$

Consistencia de sistemas lineales

Definición. Un sistema lineal es dicho consistente si tiene al menos una solución. Se le llama inconsistente si no es consistente (es decir, si no existe una solución).

Presentamos una última definición para esta entrada.

Definición.

Dos sistemas lineales se dicen equivalentes si tienen el mismo conjunto de soluciones
Sean $A$ y $B$ dos matrices del mismo tamaño. Si los sistemas $AX=0$ y $BX=0$ son equivalentes, escribiremos $A\sim B$.

Ejemplo. Un ejemplo clásico de un sistema inconsistente es

\begin{align*}
\begin{cases}
x_1=0\\
x_1=1
\end{cases}
\end{align*}

o bien

\begin{align*}
\begin{cases}
x_1 -2x_2=1\\
2 x_2-x_1=0
\end{cases}.
\end{align*}

$\triangle$

Observación. Observamos que todo sistema homogéneo siempre es consistente, ya que el vector cero (cuyas coordenadas son todas cero) satisface el sistema. A esta solución la conocemos como solución trivial. Se sigue de la proposición que un sistema consistente $AX=b$ tiene una única solución si y sólo si el sistema homogéneo asociado tiene como única solución la solución trival.

Más adelante

El principio de superposición dice que para entender las soluciones de los sistemas lineales de la forma $AX=b$, basta con entender a los homogéneos, es decir, los de la forma $AX=0$.

Nuestro siguiente paso será ver cómo podemos entender las soluciones de los sistemas lineales homogéneos. Para ello, tenemos que hablar de los sistemas que corresponden a matrices en forma escalonada reducida. La ventaja de estos sistemas es que sus soluciones son muy fáciles de entender, y para cualquier sistema de ecuaciones $AX=0$, hay uno de la forma $A_{red}X=0$, con $A_{red}$ una matriz escalonada reducida, y equivalente a $A$.

Más adelante, ya que tengamos a nuestra disposición herramientas de determinantes, hablaremos de otra forma en la que se pueden resolver sistemas de ecuaciones lineales usando la regla de Cramer.

Tarea moral

Muestra que el sistema \begin{align*}
\begin{cases}
x_1 -2x_2=1\\
2 x_2-x_1=0
\end{cases}.
\end{align*}
es inconsistente. Para ello, puedes proceder por contradicción, suponiendo que existe una solución.
Rescribe el primer ejemplo de sistemas de ecuaciones lineales en términos de vectores.
Sea $b$ un vector en $F^n$ y $I_n$ la matriz identidad en $M_n(F)$. ¿Cómo se ve de manera explícita el sistema de ecuaciones $(2I_n)X=b$? ¿Cuáles son todas sus soluciones?
Sean $A,B$ matrices de tamaño $n\times n$ tales que el sistema $ABX=0$ solo tiene como solución la solución trivial. Demuestre que el sistema $BX=0$ también tiene como única solución a la solución trivial.
Sea $A\in M_2(\mathbb{C})$ y considere el sistema homogéneo $AX=0$. Demuestre que son equivalentes:
1. El sistema tiene una única solución, la solución trivial.
2. $A$ es invertible.

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Problemas de transpuesta de matriz y matrices de bloque
Siguiente entrada del curso: Forma escalonada reducida

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Problemas de determinantes y ecuaciones lineales

Por Blanca Radillo

2 respuestas

Introducción

En esta entrada, realizaremos problemas que nos ayudarán a repasar el tema visto el pasado lunes, sobre soluciones de sistemas lineales, Teorema de Rouché-Capelli y la regla de Cramer.

Problemas de ecuaciones lineales

Una de las maneras más usuales para demostrar que un conjunto de vectores es linealmente independientes es probar que tomamos una combinación lineal de éstos tal que es igual a 0, sólo es posible si todos los coeficientes son igual a cero. Pero como ya lo hemos visto anteriormente en diversos problemas, algunas veces ésto nos genera un sistema de ecuaciones que puede ser difícil y/o tardado resolver.

Por ello, otra manera de demostrar independencia lineal es ilustrada con el siguiente problema.

Problema 1. Considera los vectores

$v_1=(1,x,0,1), \quad v_2=(0,1,2,1), \quad v_3=(1,1,1,1)$

en $\mathbb{R}^4$. Prueba que para cualquier elección de $x\in\mathbb{R}$, los vectores $v_1,v_2,v_3$ son linealmente independientes.

Solución. Sea $A$ la matriz cuyas columnas son $v_1,v_2,v_3$, es decir,

$A=\begin{pmatrix} 1 & 0 & 1 \\ x & 1 & 1 \\ 0 & 2 & 1 \\ 1 & 1 & 1 \end{pmatrix}.$

Sabemos que $v_1,v_2,v_3$ son linealmente independiente si y sólo si $\text{dim(span}(v_1,v_2,v_3))=3$, ya que $\text{rank}(A)=3$, y eso es equivalente (por la clase del lunes) a demostrar que $A$ tiene una submatriz de $3\times 3$ invertible.

Notemos que si borramos el segundo renglón, obtenemos la submatriz cuyo determinante es

$\begin{vmatrix} 1 & 0 & 1 \\ 0 & 2 & 1 \\ 1 & 1 & 1 \end{vmatrix}=-1,$

lo que implica que es invertible, y por lo tanto $v_1,v_2, v_3$ son vectores linealmente independientes.

$\square$

En este curso, los ejemplos usualmente utilizan espacios vectoriales sobre $\mathbb{R}$ o sobre $\mathbb{C}$. Como $\mathbb{R}\subset \mathbb{C}$, es natural preguntarnos si los resultados obtenidos en los problemas trabajados en $\mathbb{R}$ se cumplen en $\mathbb{C}$. En este caso particular, si las soluciones de una matriz en $M_{m,n}(\mathbb{R})$ son soluciones de la misma matriz pero vista como elemento en $M_{m,n}(\mathbb{C})$. El siguiente teorema nos da el resultado a esta pregunta.

Teorema. Sea $A\in M_{m,n}(F)$ y sea $F_1$ un campo contenido en $F$. Consideremos el sistema lineal $AX=0$. Si el sistema tiene una solución no trivial en $F_1^n$, entonces tiene una solución no trivial en $F^n$.

Demostración. Dado que el sistema tiene una solución no trivial en $F_1^n$, $r:=\text{rank}(A) < n$ vista como elemento en $M_{m,n}(F_1)$. Por el primer teorema visto en la clase del lunes, el rango es el tamaño de la submatriz cuadrada más grande que sea invertible, y eso es independiente si se ve a $A$ como elemento de $M_{m,n}(F_1)$ o de $M_{m,n}(F)$. Y por el teorema de Rouché-Capelli, el conjunto de soluciones al sistema es un subespacio de $F^n$ de dimensión $n-r>0$. Por lo tanto, el sistema $AX=0$ tiene una solución no trivial en $F^n$.

$\square$

A continuación, se mostrarán dos ejemplos de la búsqueda de soluciones a sistemas lineales donde usaremos todas las técnicas aprendidas a lo largo de esta semana.

Problema. 2 Sea $S_a$ el siguiente sistema lineal:

$\begin{matrix} x-2y+z=1 \\ 3x+2y-2z=2 \\ 2x-y+az=3 \end{matrix}.$

Encuentra los valores de $a$ para los cuales el sistema no tiene solución, tiene exactamente una solución y tiene un número infinito de soluciones.

Solución. El sistema lo podemos escribir como $AX=b$ donde

$A=\begin{pmatrix} 1 & -2 & 1 \\ 3 & 2 & -2 \\ 2 & -1 & a \end{pmatrix} \quad \text{y} \quad b=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}.$

Notemos que

$\begin{vmatrix} 1 & -2 & 1 \\ 3 & 2 & -2 \\ 2 & -1 & a \end{vmatrix}=8a-1,$

entonces si $a\neq 1/8$, $A$ es invertible, y por lo tanto $\text{rank}(A)=3$, mientras que si $a=1/8$, $A$ no es invertible y $\text{rank}(A)=2$ ya que la submatriz es invertible

$\begin{vmatrix} 1 & -2 \\ 3 & 2 \end{vmatrix}=8.$

Además, si la matriz $(A,b)$ es igual a

$\begin{pmatrix} 1 & -2 & 1 & 1 \\ 3 & 2 & -2 & 2 \\ 2 & -1 & a & 3 \end{pmatrix},$

quitando la tercera columna, obtenemos una submatriz invertible (ejercicio). Por lo tanto, $\text{rank}(A,b)=3$.

Aplicando el Teorema de Rouché-Capelli, para $a=1/8$, el sistema $AX=b$ no tiene soluciones. También podemos concluir que como $\text{rank}(A)=3$ para todo $a\neq 1/8$, el sistema tiene exactamente una solución. (Y $AX=b$ nunca tiene infinitas soluciones).

$\triangle$

Problema 3. Sean $a,b,c$ números reales dados. Resuelve el sistema lineal

$\begin{matrix} (b+c)x+by+cz=1 \\ ax+ (a+c)y+cz=1 \\ ax+by+(a+b)z=1 \end{matrix}.$

Solución. La matriz del sistema es

$A=\begin{pmatrix} b+c & b & c \\ a & a+c & c \\ a & b & a+b \end{pmatrix}.$

No es difícil ver que $\text{det}(A)=4abc$. Si $abc\neq 0$, usando la regla de Cramer, la única solución al sistema está dada por

$x=\frac{\begin{vmatrix} 1 & b & c \\ 1 & a+c & c \\ 1 & b & a+b \end{vmatrix}}{4abc}, \quad y=\frac{\begin{vmatrix} b+c & 1 & c \\ a & 1 & c \\ a & 1 & a+b \end{vmatrix}}{4abc}$

$y=\frac{\begin{vmatrix} b+c & b & 1 \\ a & a+c & 1 \\ a & b & 1 \end{vmatrix}}{4abc},$

resolviendo los determinantes obtenemos que

$x=\frac{a^2 -(b-c)^2}{4abc}, \quad y=\frac{b^2 -(a-c)^2}{4abc}, \quad z=\frac{c^2-(a-b)^2}{4abc}.$

Ahora, si $abc=0$, entonces $A$ no es invertible ($\text{rank}(A)<3$). El sistema es consistente si y sólo si $\text{rank}(A)=\text{rank}(A,b)$.

Sin pérdida de generalidad, decimos que $a=0$ (pues $abc=0$). Esto reduce el sistema a

$\begin{matrix} (b+c)x+by+cz=1 \\ c(y+z)=1 \\ b(y+z)=1 \end{matrix}.$

El sistema es consistente si $b=c$ y distintos de cero. En este caso, tenemos que $b(2x+y+z)=1$ y $b(y+z)=1$, implicando $x=0$, $y+z=1/b$. De manera similar, obtenemos las posibles soluciones si $b=0$ o si $c=0$.

Resumiendo:

Si $abc\neq 0$, el sistema tiene una solución única dada por la regla de Cramer.
Si tenemos alguno de los siguientes tres casos: caso 1) $a=0$ y $b=c \neq 0$; caso 2) $b=0$ y $a=c\neq 0$; caso 3) $c=0$ y $a=b\neq 0$, tenemos infinitas soluciones descritas como, para todo $w\in \mathbb{R}$: caso 1) $(0,w,1/b-w)$; caso 2) $(w,0,1/a-w)$; caso 3) $(w,1/a-w,0)$.
Si no se cumplen ninguno de las cuatro condiciones anteriores para $a,b,c$, el sistema no es consistente.

$\triangle$

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Determinantes en sistemas de ecuaciones lineales y regla de Cramer
Siguiente entrada del curso: Eigenvectores y eigenvalores de transformaciones y matrices

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»