Archivo de la etiqueta: pitágoras

Geometría Moderna II: Potencia de un punto

Por Armando Arzola Pérez

Deja un comentario

Introducción

En esta primera unidad abordaremos varios los temas relacionados con las circunferencias coaxiales. Para ello, iniciaremos hablando de la potencia de un punto con respecto a una circunferencia. A grandes rasgos, esto trata de lo siguiente.

Tomemos una circunferencia $\mathcal{C}$. Tomemos $P$ un punto cualquiera. Tomemos una recta $l$ por $P$ y llamemos $A$ y $B$ los puntos de intersección de $l$ con $\mathcal{C}$. Bajo estas elecciones, la potencia de $P$ será $PA\cdot PB$. Lo que veremos en esta entrada es que dicho producto es constante sin importar la elección de $l$. Para mostrar esto, introduciremos algunas definiciones y posteriormente haremos una demostración por casos.

Definición de potencia de un punto

Comenzaremos dando una primer definición de potencia, que dependerá de cierto punto, circunferencia y recta que elijamos.

Definición. Sea $\mathcal{C}$ una circunferencia, $P$ un punto y $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ en la recta $l$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C},l):=PA\cdot PB.$$

En esta definición y de aquí en adelante, a menos que se diga lo contrario, se estará trabajando con segmentos dirigidos. Es decir, estamos pensando que cada segmento tiene una dirección del primer punto al segundo. Así, por ejemplo, el valor de $PA$ dependerá de la longitud del segmento y su signo dependerá de una dirección (usualmente implícita) que se le asigne a la recta por $A$ y $P$. De este modo, tendremos, por ejemplo, que $PA=-AP$.

La definición de potencia de un punto puede simplificarse notablemente en vista de la siguiente proposición.

Proposición. La potencia de un punto con respecto a una circunferencia no depende de la recta elegida. Es decir, tomemos $\mathcal{C}$ una circunferencia, $P$ un punto y $l,m$ rectas. Supongamos que los puntos de intersección de $l$ con $\mathcal{C}$ son $A$ y $B$; y que los puntos de intersección de $m$ con $\mathcal{C}$ son $C$ y $D$ (en caso de tangencias, repetimos los puntos). Entonces: $$PA\cdot PB = PC\cdot PD.$$

Demostración. Haremos la demostración por casos de acuerdo a cuando $P$ está dentro o fuera de la circunferencia, o sobre ella.

Dentro de la circunferencia:

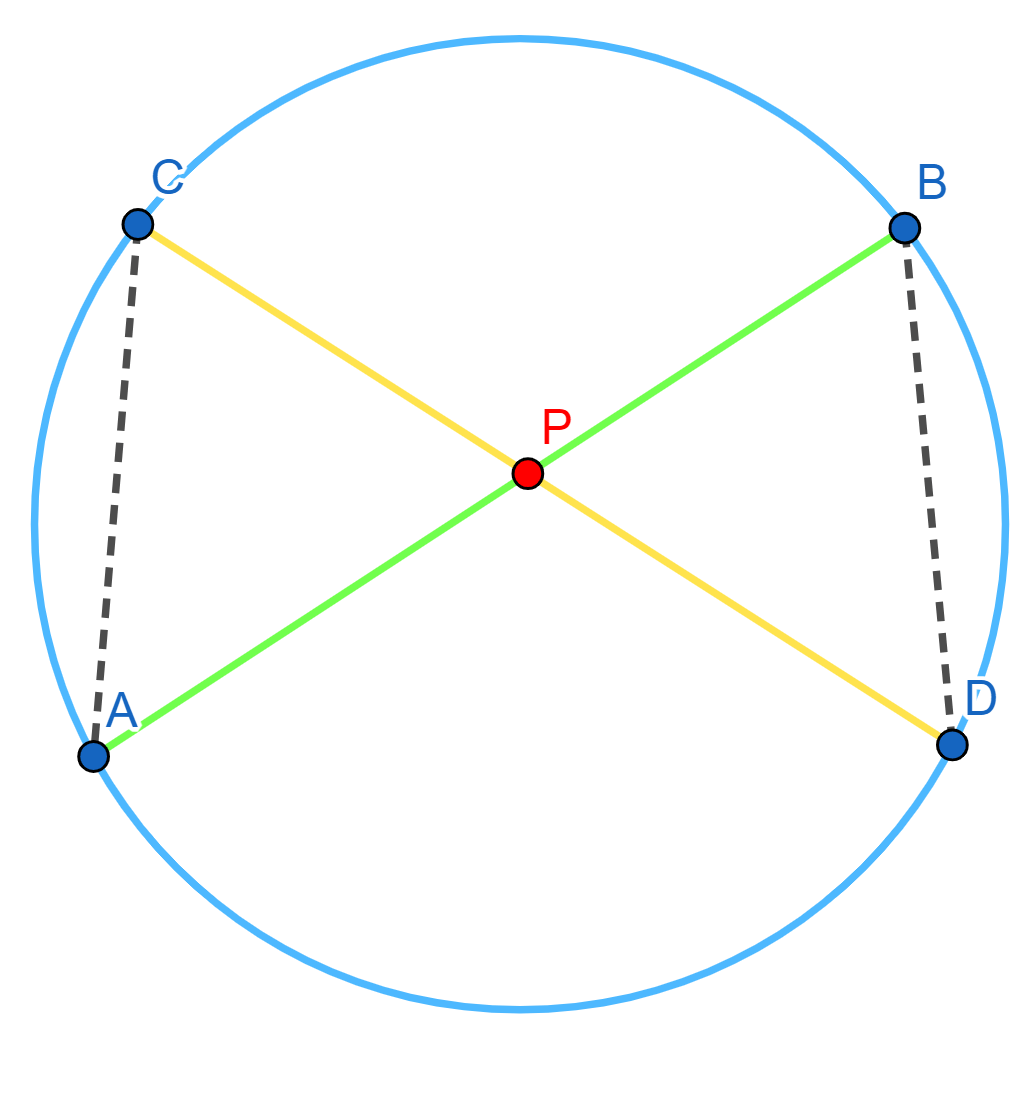
Tomemos las cuerdas $AB$ y $CD$ en la circunferencia, las cuales se cortan en $P$. Los triángulos $\triangle APC$ y $\triangle DPB$ son semejantes ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está dentro de la circunferencia.
  1. $\angle PAC = \angle PDB $ por abrir el mismo arco $\overline{BC}$.
  2. $\angle APC = \angle BPD $ por ser opuestos al vértice.
  3. $\angle PCA = \angle PBD $ por abrir mismo arco $\overline{AD}$.

Entonces de la semejanza $\triangle APC \cong \triangle DPB $ tenemos que

$\frac{PA}{PD}=\frac{PC}{PB},$

de donde obtenemos la igualdad $PA\cdot PB =PC \cdot PD$ deseada.

Fuera de la circunferencia:

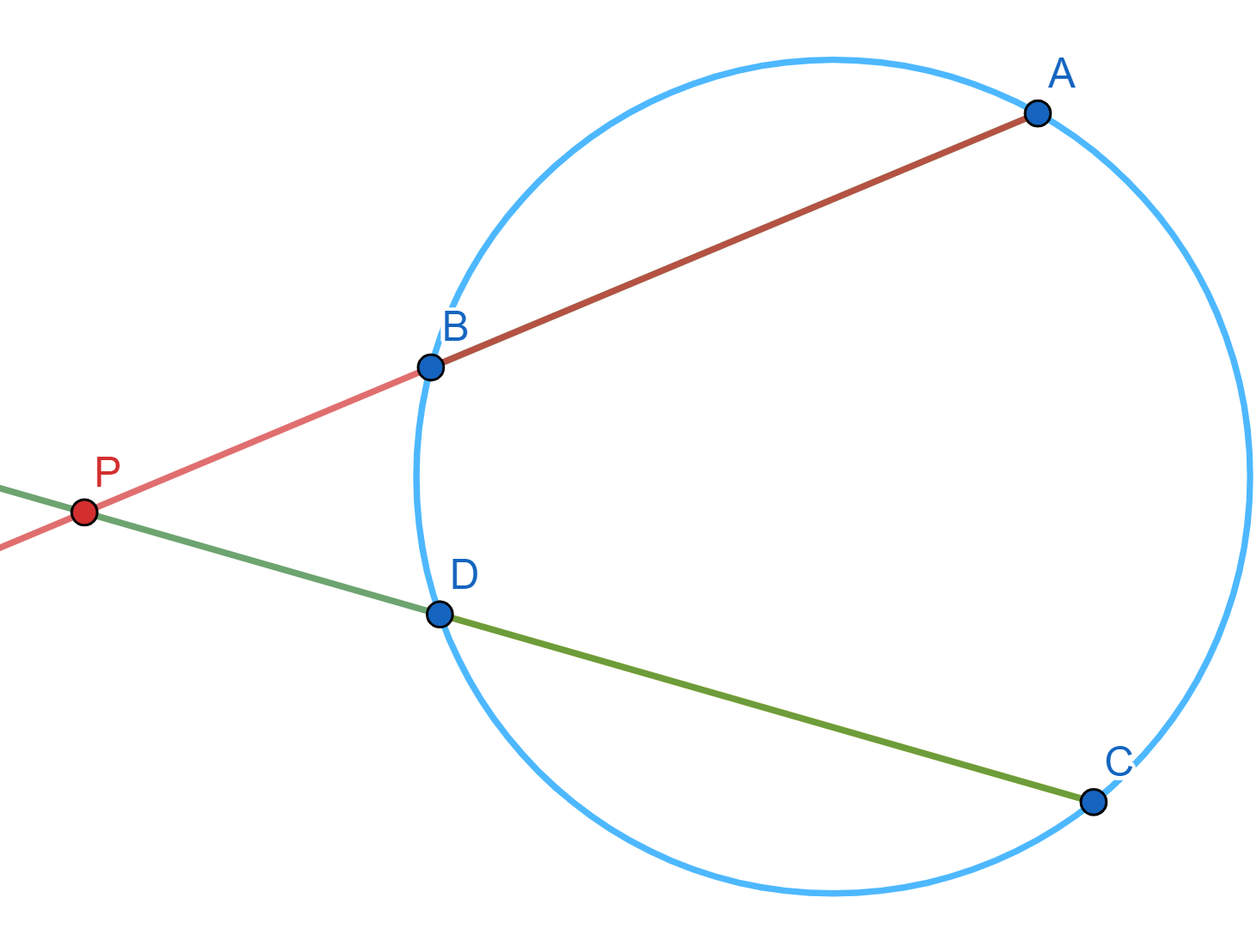
Ahora, $AB$ y $CD$ son dos secantes que se intersecan en $P$, pero con $P$ exterior a $\mathcal{C}$. Tenemos que $\triangle APC $ y $\triangle DPB $ son semejantes, ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está fuera de la circunferencia.
  1. El cuadrilátero $\square ABDC$ es cíclico, entonces: $\angle ACD + \angle ABD = 180^\circ$ y $\angle ABD + \angle DBP = 180^\circ $, de donde $\angle DBP = \angle ACD$.
  2. $\angle BPD$ y $\angle CPA$ son los mismos ángulos.

Entonces $\frac{PA}{PC}=\frac{PD}{PB},$ de donde se obtiene la igualdad buscada $PA\cdot PB=PC\cdot PD.$

Sobre la circunferencia:

Este caso es sencillo pues sin importar las secantes tomadas, en cada una hay un punto igual a $P$ y por lo tanto una distancia igual a cero. De este modo, $PA\cdot PB=0=PC\cdot PD$.

$\square$

Nota que las demostraciones anteriores sirven aunque $l$ ó $m$ sean tangentes, sólo que hay que hacer ligeras adaptaciones sobre los ángulos usados y los motivos por los que son iguales. Enunciaremos el caso de la tangencia un poco más abajo.

En vista de la proposición anterior, podemos simplificar nuestra definición notablemente.

Definición. Sea $\mathcal{C}$ una circunferencia y $P$ un punto. Tomemos $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C}):=PA\cdot PB.$$

La potencia queda bien definida sin importar la recta $l$, debido a la proposición anterior.

El signo de la potencia

En esta definición estamos usando segmentos dirigidos, y eso nos lleva a que la potencia de un punto puede tener distintos signos. El comportamiento queda determinado por el siguiente resultado.

Proposición. La potencia de un punto $P$ con respecto a una circunferencia $\mathcal{C}$ es positiva, negativa o cero, de acuerdo a si el punto $P$ está fuera de $\mathcal{C}$, dentro de ella, o sobre ella, respectivamente.

Demostración. Veamos esto caso por caso.

  • Sea $P$ un punto externo a $\mathcal{C}$. Entonces $PA$ y $PB$ tienen la misma orientación y por lo tanto el mismo signo. Además, como $P$ no está sobre $\mathcal{C}$, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})> 0$.
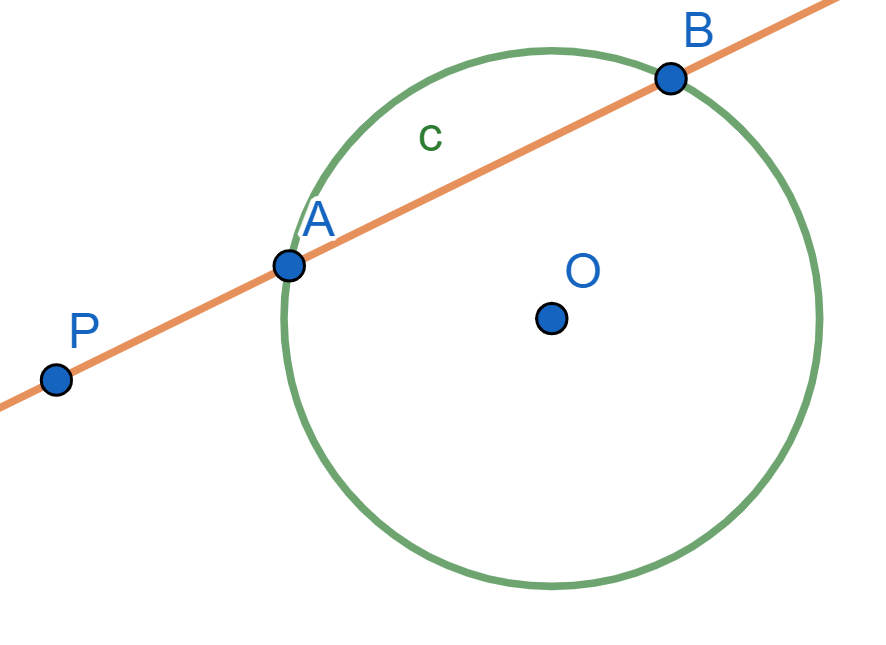
Geometría Moderna II: Potencia de un punto respecto a un punto externo.
  • Sea $P$ un punto interno a $\mathcal{C}$. Entonces $PA$ está dirigido hacia un lado y $PB$ está dirigido hacia el otro, de modo que tienen signo contrario. Además, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})<0$.
Geometría Moderna II: Potencia de un punto respecto a un punto interno de la circunferencia.
  • Finalmente, sea $P$ un punto sobre $\mathcal{C}$. Esto quiere decir que alguno de los puntos $A$ o $B$ es $P$ (quizás ambos, si $l$ es tangente). Así, $PA=0$ ó $PB=0$. De este modo $\text{Pot}(P,\mathcal{C})=0$.
Geometría Moderna II: Potencia de un punto que está sobre la circunferencia.

$\square$

Otras fórmulas para la potencia

La potencia es invariante sin importar la recta elegida. De este modo, podemos elegir a una recta tangente y obtener una fórmula para la potencia en términos de la longitud de dicha tangente.

Proposición. Sea $\mathcal{C}$ una circunferencia. Para un punto $P$ fuera de $\mathcal{C}$, su potencia es igual al cuadrado de la longitud de una tangente de él a la circunferencia.

Es decir, sea $T$ un punto sobre la circunferencia tal que $PT$ sea tangente a $\mathcal{C}$. Entonces, $\text{Pot}(P,\mathcal{C})=PT^2$.

Imagen representativa de la Proposición 2.

El resultado se sigue de llevar al límite lo que ya probamos en la proposición de invarianza de la potencia. Pero a continuación damos un argumento alternativo.

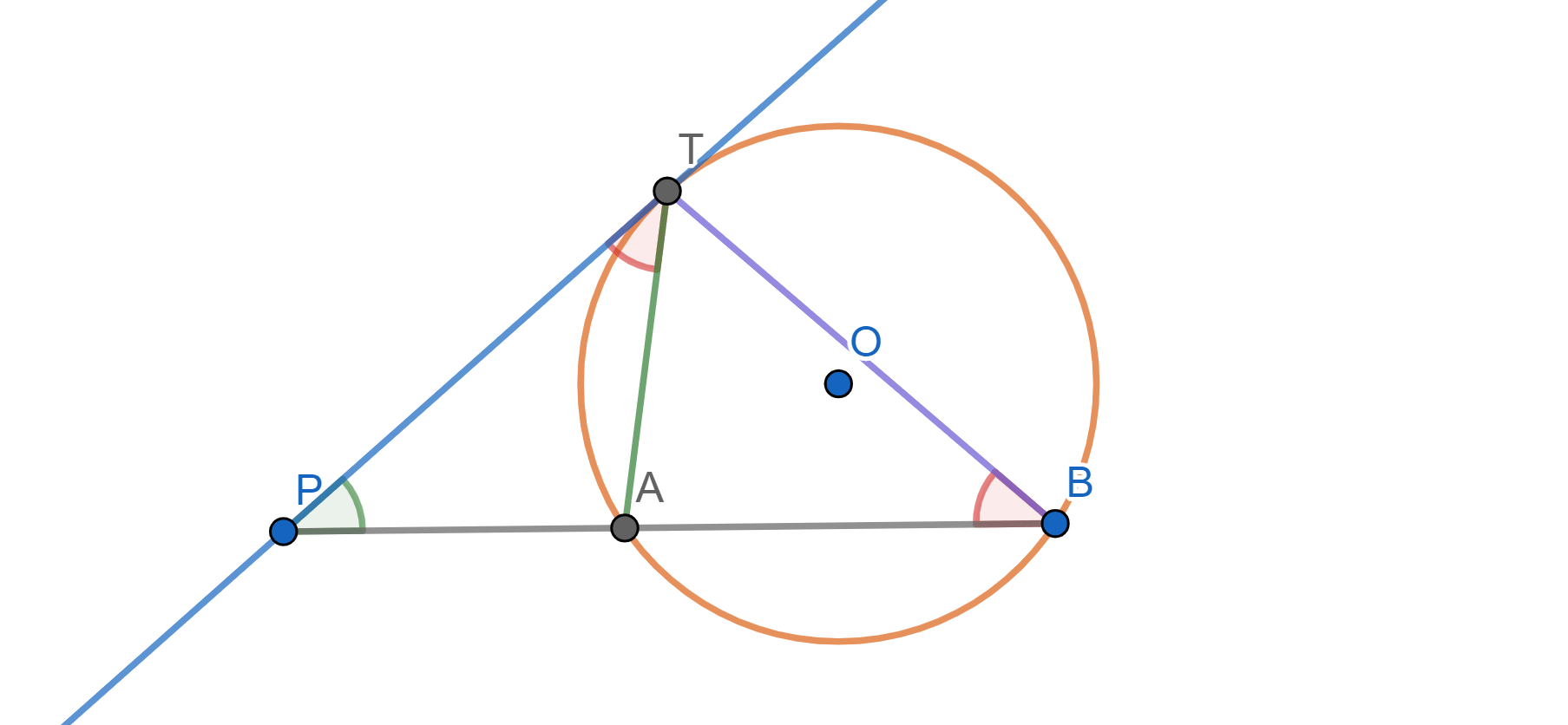
Demostración. Tracemos otra recta por $P$ que no sea tangente a $\mathcal{C}$ y cuyos puntos de intersección con $\mathcal{C}$ son $A$ y $B$ como en la figura. Tenemos que mostrar que $PA\cdot PB =PT^2$.

El ángulo $\angle PTA$ es semi-inscrito y es igual al ángulo inscrito $ \angle TBA$, pues ambos tienen el mismo arco $\overline{AT}$.

Entonces los triángulos $\triangle APT$ y $\triangle TPB$ comparten el ángulo con vértice en $P$ y $\angle PTA=\angle TBA$. Por ello, se tiene que $\triangle APT \cong \triangle TPB $ son semejantes y sus lados son proporcionales: $\frac{PA}{PT} = \frac{PT}{PB}$. De aquí, $$PT^2=PT\cdot PT=PA\cdot PB=\text{Pot}(P,\mathcal{C}).$$

$\square$

También es posible conocer la potencia de un punto hacia una circunferencia si conocemos el radio de la circunferencia y la distancia del punto al centro.

Proposición. Sea $\mathcal{C}$ una circunferencia de centro $O$ y radio $r$. Sea $P$ un punto en cualquier posición. La potencia de $P$ con respecto a $\mathcal{C}$ es $$\text{Pot}(P,\mathcal{C}) = OP^2 – r^2.$$

Demostración. Haremos la demostración por casos

Dentro de la circunferencia:

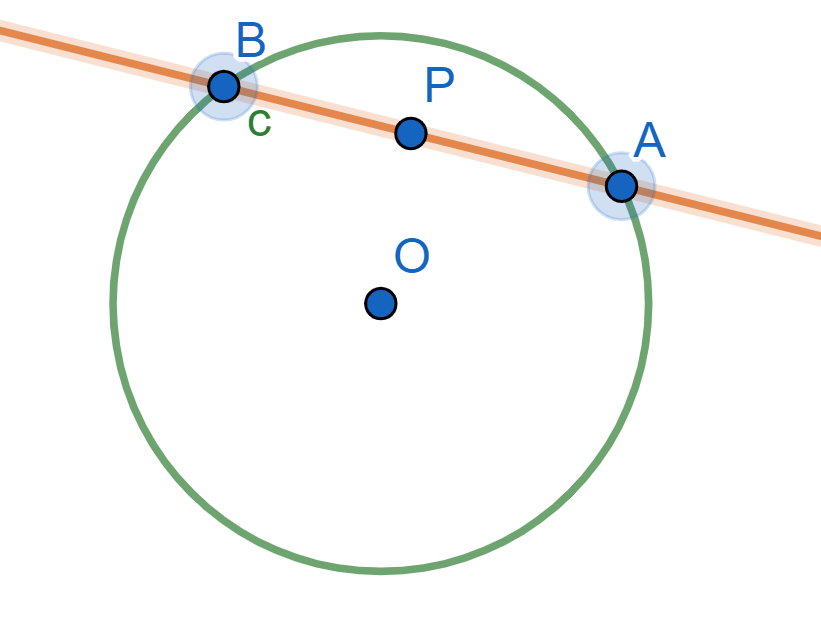
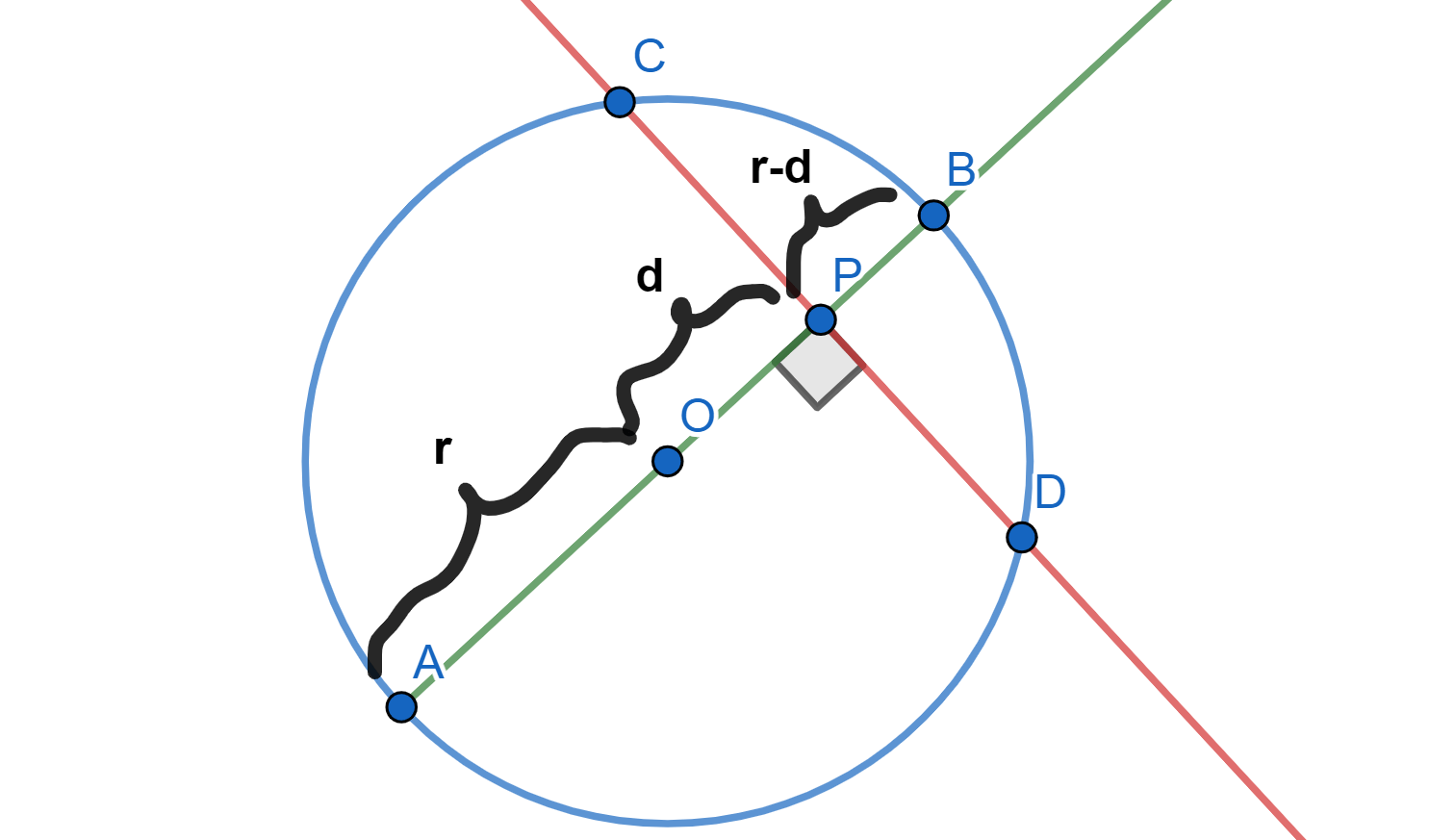
Sea $AB$ la cuerda que pasa por el centro $O$ y $P$ (si $O=P$, tomamos cualquier cuerda $AB$ por el centro). Supongamos sin pérdida de generalidad que la recta está dirigida de $A$ a $B$. Tenemos que $AO=r>0$ y llamemos $d=OP>0$. De aquí, $PB=r-d>0$. La siguiente figura resume estas igualdades.

Potencia de un punto imagen de Proposición 3 cuando un punto está dentro de la circunferencia.

La potencia desde $P$ sería entonces, cuidando los signos:

\begin{align*}
PA\cdot PB &= (PO+OA)(PB)\\
&=(-d-r)(r-d)\\
&=-(d+r)(r-d)\\
&=-(r^2-d^2)\\
&=d^2-r^2\\
&=OP^2-r^2.
\end{align*}

Así, $\text{Pot}(P,\mathcal{C})=OP^2-r^2$.

Fuera de la circunferencia:

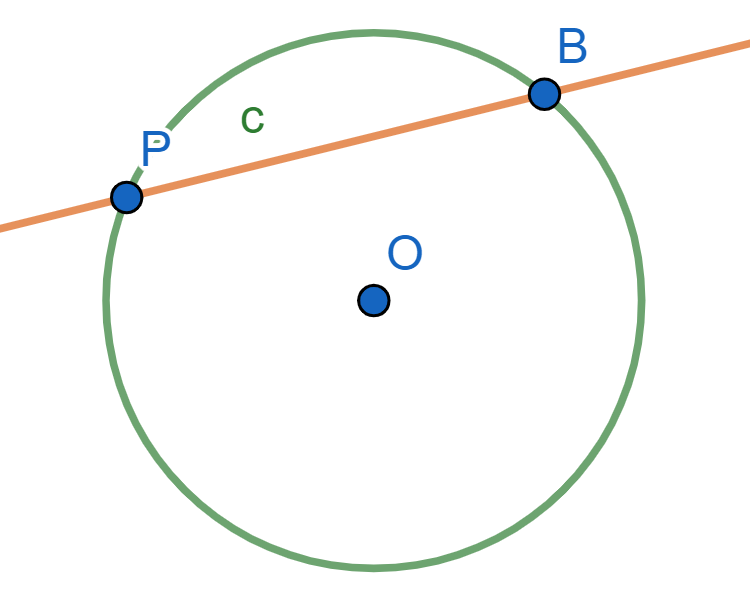
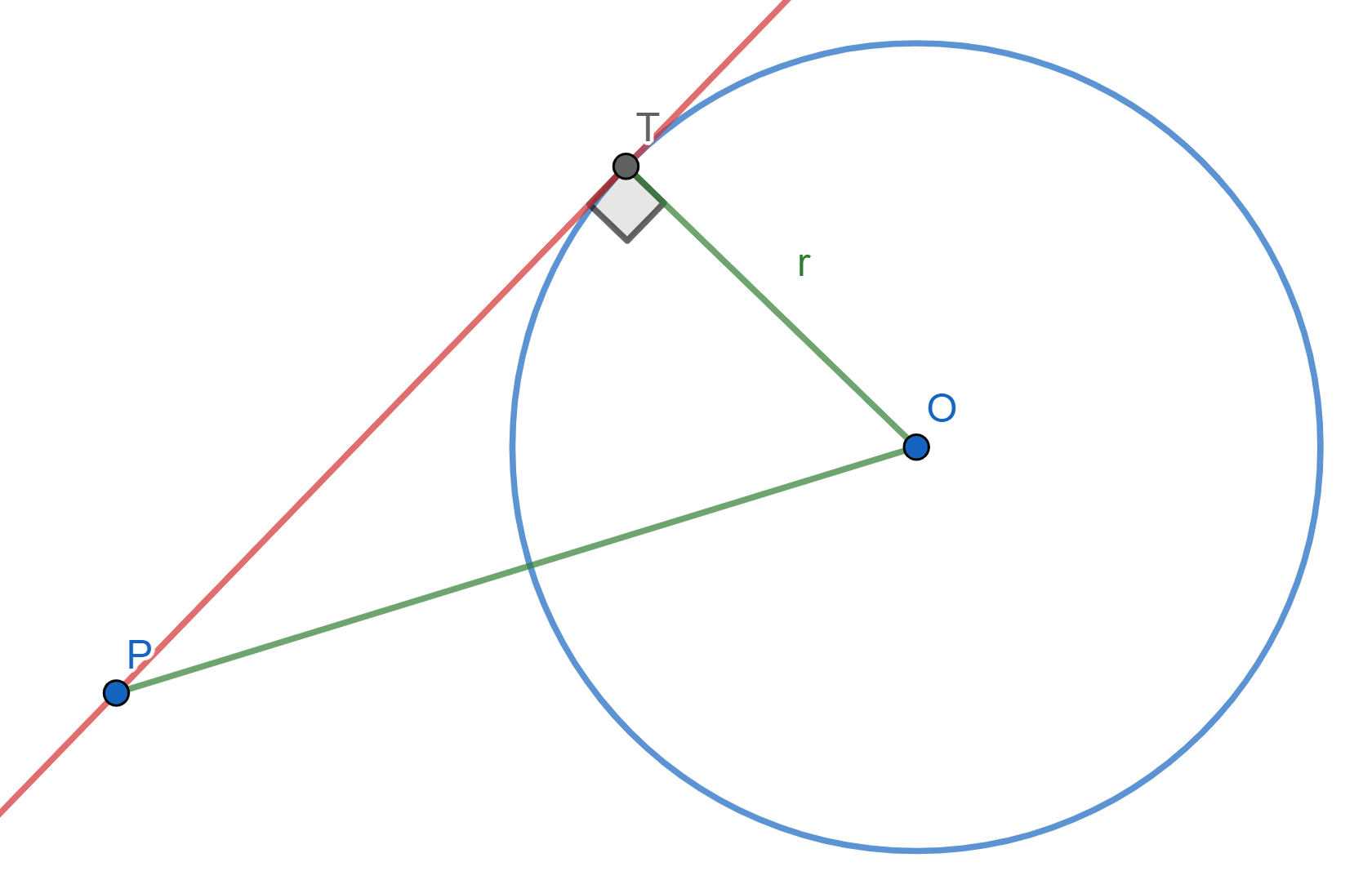
Ahora desde $P$ tracemos una tangente $PT$ a $\mathcal{C}$ con $T$ sobre $\mathcal{C}$. Como $\angle PTO =90^o$, entonces $\triangle POT$ es un triángulo rectángulo.

Potencia de un punto imagen de Proposición 3 cuando un punto está fuera de la circunferencia.

Por el teorema de Pitágoras y la expresión de potencia en términos de la tangente: $$OP^2=r^2+PT^2=r^2+\text{Pot}(P,\mathcal{C}).$$ Despejando, obtenemos la expresión deseada: $$\text{Pot}(P,\mathcal{C})=OP^2-r^2.$$

Sobre la circunferencia:

Este caso es sencillo, pues sabemos que la potencia de $P$ debe ser cero. Pero además, como $P$ está en la circunferencia, entonces $OP=r$, de modo que $OP^2-r^2=0$, y entonces la expresión también es lo que queremos.

$\square$

Más adelante…

Seguiremos abordando el tema de potencia de un punto y veremos cómo a partir de él se define el eje radical de dos circunferencias.

Entradas relacionadas

Álgebra Lineal I: Formas cuadráticas, propiedades, polarización y Gauss

Por Leonardo Ignacio Martínez Sandoval

8 respuestas

Introducción

En la entrada anterior hablamos acerca de formas bilineales y comenzamos a hablar de formas cuadráticas. Discutimos cómo a partir de estas nociones a la larga podremos hablar de geometría y cálculo en espacios vectoriales. El objetivo de esta entrada es entender mejor a las formas cuadráticas y su relación con formas bilineales.

Lo primero que haremos es demostrar la identidad de polarización, que a grandes rasgos dice que hay una biyección entre las formas bilineales simétricas y las formas cuadráticas. Veremos algunos ejemplos concretos de esta biyección. A partir de ella demostraremos algunas propiedades de formas cuadráticas. Finalmente, hablaremos brevemente de un bello resultado de Gauss que caracteriza las formas cuadráticas en $\mathbb{R}^n$ en términos de formas lineales, de las cuales discutimos mucho cuando hablamos de espacio dual.

Como pequeño recordatorio de la entrada anterior, una forma bilineal de un espacio vectorial $V$ es una transformación $b:V\times V \to \mathbb{R}$ tal que cada que fijamos una coordenada, es lineal en la otra. Esta forma es simétrica si $b(x,y)=b(y,x)$ para cada par de vectores $x,y$ en $V$. Una forma cuadrática de $V$ es una transformación $q:V\to \mathbb{R}$ tal que $q(x)=b(x,x)$ para alguna forma bilineal $b$.

Formas cuadráticas y polarización

En la entrada anterior enunciamos el siguiente teorema, que mostraremos ahora.

Teorema (identidad de polarización). Sea $q:V\to \mathbb{R}$ una forma cuadrática. Existe una única forma bilineal simétrica $b:V\times V \to \mathbb{R}$ tal que $q(x)=b(x,x)$ para todo vector $x$. Esta forma bilineal está determinada mediante la identidad de polarización $$b(x,y)=\frac{q(x+y)-q(x)-q(y)}{2}.$$

Demostración. Tomemos una forma cuadrática $q$ de $V$. Por definición, está inducida por una forma bilineal $B$ de $V$, es decir, $q(x)=B(x,x)$. Definamos la transformación $b$ mediante $$b(x,y)=\frac{q(x+y)-q(x)-q(y)}{2}.$$ Comencemos probando que $b$ es una transformación bilineal simétrica. Notemos que:
\begin{align*}
b(x,y)&=\frac{q(x+y)-q(x)-q(y)}{2}\\
&=\frac{B(x+y,x+y)-B(x,x)-B(y,y)}{2}\\
&=\frac{B(x,x)+B(x,y)+B(y,x)+B(y,y)-B(x,x)-B(y,y)}{2}\\
&=\frac{B(x,y)+B(y,x)}{2}.
\end{align*}

De aquí es muy claro que $b$ es forma bilineal, pues fijando $x$, set tiene que $b(x,y)$ es combinación lineal de dos formas lineales en $y$; y fijando $y$, se tiene que $b(x,y)$ es combinación lineal de dos formas lineales en $x$. Además, de esta igualdad (o directo de la definición de $b$) es claro que $b(x,y)=b(y,x)$.

También de esta igualdad obtenemos que $$b(x,x)=B(x,x)=q(x).$$

Para mostrar la unicidad, notemos que cualquier forma bilineal simétrica $b’$ tal que $b'(x,x)=q(x)$ debe satisfacer, como en las cuentas que hicimos arriba, que
\begin{align*}
q(x+y)&=b'(x+y,x+y)\\
&=q(x)+q(y)+b'(x,y)+b'(y,x)\\
&=q(x)+q(y)+2b'(x,y).
\end{align*}

De aquí, despejando $b’$, se obtiene que debe tener la forma de $b$.

$\square$

El teorema anterior justifica la siguiente definición.

Definición. Dada una forma cuadrática $q$ de $V$, a la única forma bilineal simétrica $b$ de $V$ tal que $q(x)=b(x,x)$ le llamamos la forma polar de $q$.

Ejemplo 1. En el espacio vectorial $\mathbb{R}^n$, la transformación $q:\mathbb{R}^n\to \mathbb{R}$ dada por $$q(x_1,\ldots,x_n)=x_1^2+\ldots+x_n^2.$$ es una forma cuadrática. Su forma polar es la forma bilineal producto punto que manda a $x=(x_1,\ldots,x_n)$ y $y=(y_1,\ldots,y_n)$ a $$b(x,y)=x_1y_1+\ldots+x_ny_n.$$

Esto coincide con la construcción dada por la identidad de polarización, ya que \begin{align*}q(x+y)-q(x)-q(y)&=\sum_{i=1}^n (x_i+y_i)^2-x_i^2-y_i^2 \\&= \sum_{i=1}^n x_iy_i\end{align*}

$\triangle$

Ejemplo 2. En el espacio vectorial $\mathbb{R}[x]$ de polinomios con coeficientes reales, la transformación $Q$ dada por $$Q(p)=p(0)p(1)+p(2)^2$$ es una forma cuadrática. Para encontrar a su forma bilineal polar, usamos la identidad de polarización
\begin{align*}
B(p,q)&=\frac{Q(p+q)-Q(p)-Q(q)}{2}\\
&=\frac{(p+q)(0)(p+q)(1)+(p+q)(2)^2-p(0)p(1)-p(2)^2-q(0)q(1)-q(2)^2}{2}\\
&=\frac{p(0)q(1)+q(0)p(1)+2p(2)q(2)}{2}\\
&=\frac{p(0)q(1)}{2}+\frac{p(1)q(0)}{2}+p(2)q(2).
\end{align*}

$\triangle$

Propiedades de formas cuadráticas

Si $q$ es una forma cuadrática, $x$ es un vector y $c$ es un real, tenemos que $q(cx)=c^2q(x)$, pues sale una $c$ por cada una de las coordenadas de la forma bilineal asociada. En particular, $q(-x)=q(x)$.

La identidad de polarización nos permite probar otras propiedades de formas bilineales y formas cuadráticas.

Proposición. Sea $q$ una forma cuadrática en $V$ con forma polar $b$. Entonces:

  • Para todo par de vectores $x$ y $y$ en $V$, se tiene que $$b(x,y)=\frac{q(x+y)-q(x-y)}{4}.$$
  • (Ley del paralelogramo) Para todo par de vectores $x$ y $y$ en $V$, se tiene que $$q(x+y)+q(x-y)=2(q(x)+q(y)).$$
  • (Teorema de Pitágoras) Para vectores $x$ y $y$ tales que $b(x,y)=0$, se tiene que $$q(x+y)=q(x)+q(y).$$
  • (Diferencia de cuadrados) Para todo par de vectores $x$ y $y$ en $V$, se tiene que $b(x+y,x-y)=q(x)-q(y).$

Demostración. Por la identidad de polarización tenemos que $$b(x,y)=\frac{q(x+y)-q(x)-q(y)}{2},$$ y como $q(y)=q(-y)$, tenemos también por la identidad de polarización que \begin{align*}-b(x,y)&=b(x,-y)\\&=\frac{q(x-y)-q(x)-q(y)}{2}.\end{align*}

Restando la segunda ecuación de la primera, obtenemos la primer propiedad. Sumando ambas obtenemos la ley del paralelogramo.

El teorema de Pitágoras es una consecuencia directa de la identidad de polarización.

La identidad de diferencia de cuadrados es una consecuencia de la primer propiedad aplicada a los vectores $x+y$ y $x-y$, y de usar que $q(2x)=4q(x)$ y que $q(2y)=4q(y)$.

$\square$

Forma de las formas cuadráticas

Otra consecuencia de la identidad de polarización es que establece una biyección entre las formas cuadráticas y las formas simétricas bilineales. Esta asociación nos permite decir cómo se ven exactamente las formas cuadráticas en espacios vectoriales de dimensión finita.

Toda forma cuadrática viene de una forma bilineal simétrica. En la entrada anterior, mencionamos que para definir una forma bilineal simétrica en un espacio vectorial $V$ de dimensión $n$, basta tomar una base $\{e_1,\ldots,e_n\}$ de $V$ y decidir los valores $b_{ij}$ de $b(e_i,e_j)$ para $1\leq i \leq j \leq n$. Como $b$ es simétrica, para $j<i$ se tendría que $b(e_i,e_j)=b(e_j,e_i)$, es decir, que $b_{ji}=b_{ij}$.

De esta forma, para todo vector $v$ en $V$ podemos encontrar el valor de $q(v)$ expresando $v$ en la base $\{e_1,\ldots,e_n\}$, digamos, $$v=a_1e_1+\ldots+a_ne_n,$$ de donde $$q(v)=\sum_{i=1}^n b_{ii} a_i^2 + 2 \sum_{1\leq i < j \leq n} b_{ij} a_i a_j.$$

Ejemplo. Toda forma cuadrática en $\mathbb{R}^3$ se obtiene de elegir reales $a,b,c,d,e,f$ y definir $$q(x,y,z)=ax^2+by^2+cz^2+2dxy+2eyz+2fzx.$$ La forma polar de $q$ es la forma bilineal $B$ tal que para la base canónica $e_1,e_2,e_3$ de $\mathbb{R}^3$ hace lo siguiente

\begin{align*}
B(e_1,e_1)&=a\\
B(e_2,e_2)&=b\\
B(e_3,e_3)&=c\\
B(e_1,e_2)&=B(e_2,e_1)=d\\
B(e_2,e_3)&=B(e_3,e_2)=e\\
B(e_3,e_1)&=B(e_1,e_3)=f.
\end{align*}

$\triangle$

Teorema de Gauss de formas cuadráticas (opcional)

Para esta sección, fijemos al espacio vectorial como $\mathbb{R}^n$. Hay una forma muy natural de construir formas cuadráticas a partir de formas lineales. Tomemos números reales $\alpha_1,\ldots, \alpha_r$ y formas lineales $l_1,\ldots,l_r$. Consideremos $$q(x)=\alpha_1l_1(x)^2+\ldots+\alpha_r l_r(x)^2.$$ Se tiene que $q$ es una forma cuadrática. La demostración de ello es sencillo y se queda como tarea moral.

Lo que descubrió Gauss es que todas las formas cuadráticas se pueden expresar de esta forma, y de hecho, es posible hacerlo usando únicamente formas lineales que sean linealmente independientes y coeficientes $1$ y $-1$.

Teorema (clasificación de Gauss de formas cuadráticas). Sea $q$ una forma cuadrática en $\mathbb{R}^n$. Entonces, existen enteros no negativos $r$ y $s$, y formas lineares $l_1,\ldots,l_r,m_1,\ldots,m_s$ en $(\mathbb{R}^n)^\ast$, todas ellas linealmente independientes, tales que $$q=l_1^2+\ldots+l_r^2-m_1^2-\ldots-m_s^2.$$

Hay un pequeño refinamiento de este teorema, demostrado por Sylvester.

Teorema (teorema de la inercia de Sylverster). Los números $r$ y $s$ en el teorema de clasificación de Gauss de formas cuadráticas son únicos.

Ejemplo. Tomemos la forma cuadrática en $\mathbb{R}^3$ dada por $q(x,y,z)=xy+yz+zx$. Por el teorema de Gauss, esta forma se debe de poder poner como combinación lineal de cuadrados de formas lineales independientes. En efecto, tenemos que: $$xy+yz+zx=\left(\frac{2x+y+z}{2}\right)^2-\left(\frac{y-z}{2}\right)^2-x^2,$$ en donde
\begin{align*}
(x,y,z)&\mapsto \frac{2x+y+z}{2},\\
(x,y,z) &\mapsto \frac{y-z}{2}\quad \text{ y }\\
(x,y,z)&\mapsto x
\end{align*}
son formas lineales linealmente independientes.

$\triangle$

Más adelante…

En esta entrada estudiamos a fondo la identidad de polarización; esto nos permitió concluir que existe una biyección entre las funciones bilineales simétricas y las formas cuadráticas. También, pusimos mucho énfasis en ejemplos concretos de esta biyección.

Con esto estamos listos para empezar a pensar en cómo haríamos geometría o cálculo en espacios vectoriales. Abordaremos estos temas al final de esta unidad. En la siguiente entrada hablaremos del producto interior.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Verifica que las formas cuadráticas de los ejemplos del teorema de polarización en efecto son formas cuadráticas.
  • Muestra que $q(x,y)=3x^2-y^2+7y$ no es una forma cuadrática.
  • Muestra que si $\alpha_1,\ldots, \alpha_r$ son reales y tomamos formas lineales $l_1,\ldots,l_r$ en $\mathbb{R}^n$, entonces $$q(x)=a_1l_1(x)^2+\ldots+\alpha_r l_r(x)^2$$ es una forma cuadrática.
  • ¿Quién es la forma polar de la forma cuadrática $Q(f)=\int_{0}^1 f^2(x)\, dx$ en el espacio vectorial de funciones continuas en el intervalo $[0,1]$?

Una demostración algorítmica del teorema de Gauss se puede encontrar en la Sección 10.1 del libro de Álgebra Lineal de Titu Andreescu.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Seminario de Resolución de Problemas: El teorema fundamental del cálculo

Por Fabian Ferrari

Deja un comentario

Introducción

Ya platicamos de continuidad, diferenciabilidad e integrales, así como de otros temas de cálculo. En esta sección reuniremos varias de estas ideas a través de uno de los resultados más importantes: el teorema fundamental del cálculo. Este teorema nos exhibe la relación que hay entre la derivada y la integral, distinguiéndolas como procedimientos inversos el uno del otro.

El teorema nos dice que si tenemos una función $F(x)$ derivable sobre un intervalo $[a, b]$, entonces

\begin{equation*}
\int_{a}^{b} \! F^\prime(t) \, dt = F(b)-F(a).
\end{equation*}

Ahora bien, si nuestra función $F(t)$ es derivable en $[0,x]$, tenemos que

\begin{equation*}
\int_{0}^{x} \! F^\prime(t) \, dt = F(x)-F(0),
\end{equation*}

a lo que le sigue que

\begin{equation*}
F(x)=\int_{0}^{x} \! F^\prime(t) \, dt + F(0).
\end{equation*}

Esto nos recuerda a la constante de integración

\begin{equation*}
F(x)=\int_{0}^{x} \! F^\prime(t) \, dt + C.
\end{equation*}

Es decir, tenemos que $C=F(0)$.

Aquí en el blog, en la entrada «Teoremas fundamentales de los cuadraditos» damos la intuición acerca de este teorema, comenzando con el caso discreto. Puedes leerlo antes de continuar.

Usar el teorema fundamental del cálculo para obtener una identidad trigonométrica

Veamos un ejemplo. Tenemos que la derivada de la función $F(t)=\sin^2 t$ es $F^\prime (t)=2\cos t\sin t$. Por el teorema fundamental del cálculo, la integral de $F'(t)$ en el intervalo $[0,x]$ está dada por

\begin{equation*}
\int_{0}^{x}\! 2 \sin t \cos t \, dt=\sin^2x,
\end{equation*}

en donde usamos que $F(0)=\sin^2(0)=0$.

Por otro lado, resolviendo la integral utilizando el cambio de variable $u=\cos t$, tenemos que $$\int_{0}^{x}\! 2 \sin t \cos t \, dt= \left. -\cos^2t \right |_0^x= -\cos^2x+1.
$$

Igualando ambos valores de la integral, tenemos que $\sin^2x=-\cos^2 x+1$. De aquí obtenemos la identidad trigonométrica pitagórica $\sin^2 x+\cos^2x=1$ para toda $x$.

Veamos ahora un problema en el que, mediante el problema fundamental del cálculo,

Problema. Aplicando el teorema fundamental del calculo halla $$\int_{a}^{b}\! \sec x\, dx.$$

Sugerencia pre-solución. Formula un problema equivalente multiplicando y dividiendo la expresión por $\sec x + \tan x$. Intenta identificar la expresión resultante como la derivada de otra función.

Solución. Para resolver este problema tenemos que hallar una función $F(x)$ de tal forma que $F^\prime (x)= \sec x$.

Para ello, tenemos que notar que

\begin{align*}
\sec x &=\sec x \left(\frac{ \sec x + \tan x}{\sec x+ \tan x}\right)\\ &=\frac{\sec^2x+\sec x \tan x}{\sec x+\tan x}.
\end{align*}

Y entonces la derivada de $\ln (\sec x + \tan x)$ es igual a

\begin{align*}
\left(\frac{1}{\sec x + \tan x}\right)&(\sec^2x+\sec x \tan x)\\
&=\frac{\sec^2x+\sec x \tan x}{\sec x+\tan x}\\&=\sec x.
\end{align*}

Proponemos a la función

\begin{equation*}
F(x)=\ln (\sec x + \tan x)
\end{equation*}

dado que

\begin{equation*}
F^\prime (x)=\sec x.
\end{equation*}

Ahora, aplicando el teorema fundamental del cálculo tenemos que

\begin{align*}
\int_{a}^{b}\! \sec x\, dx&=F(b)-F(a)\\&=\ln (\sec b + \tan b)-\ln (\sec a + \tan a)
\end{align*}

$\square$

Segundo teorema fundamental del cálculo

Veamos una implicación del teorema fundamental del cálculo, que también se le conoce como el «segundo teorema fundamental del cálculo».

Para una función $f: [a,b] \to \mathbb{R}$ continua en el intervalo $[a,b]$ se tiene que:

\begin{equation*}
\frac{d}{dx}\left(\int_{a}^{x}\! f(t)\, dt\right)=f(x)
\end{equation*}

Problema. Determina $$\frac{d}{dx}\left(\int_{3x-1}^{0} \! \frac{1}{t+4}\, dt\right).$$

Sugerencia pre-solución. Usa el segundo teorema fundamental del cálculo y la regla de la cadena.

Solución. Como $$\int_{3x-1}^{0} \! \frac{1}{t+4}\, dt=-\int_{0}^{3x-1} \! \frac{1}{t+4}\, dt,$$ tenemos entonces que

$$\frac{d}{dx}\left(\int_{3x-1}^0 \frac{1}{t+4} \, dt\right)= – \frac{d}{dx}\left(\int_{0}^{3x-1} \frac{1}{t+4} \, dt\right).$$

Por otro lado, consideremos las funciones

\begin{align*}
f(x)&=\int_{0}^{x} \! \frac{1}{t+4}\, dt \quad \text{y}\\
g(x)&=3x-1.
\end{align*}

Aplicando el teorema fundamental del cálculo y derivando tenemos que

\begin{align*}
f^\prime (x)&=\frac{1}{x+4} \quad \text{y}\\
g^\prime (x)&=3.
\end{align*}

Notemos que

\begin{align*}
(f \circ g)(x)&=f( g(x) )\\&=f(3x-1)\\&=\int_{0}^{3x-1}\! \frac{1}{t+4}\, dt.
\end{align*}

Así, aplicando la regla de la cadena, tenemos que

\begin{align*}
-\frac{d}{dx}\left(\int_{0}^{3x-1} \! \frac{1}{t+4}\, dt\right)&=-\frac{d}{dx}(f(g(x))\\&=-f^\prime (g(x)) g^\prime(x)\\
&=-\frac{1}{(3x-1)+4}\cdot 3\\
&=-\frac{1}{x+1}.
\end{align*}

$\square$

Veamos un último problema en el que se usa la segunda forma del teorema fundamental del cálculo.

Problema: Supongamos que $f$ es una función continua para toda $x$, la cual satisface la ecuación

\begin{equation}
\int_{0}^{x} \! f(t)\, dt= \int_{x}^{1} \! t^2f(t) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C,
\end{equation}

donde $C$ es una constante. Encuentra la forma explícita de la función $f(x)$ y determina el valor de la constante $C$.

Sugerencia pre-solución.

Solución. De la ecuación, tenemos lo siguiente

\begin{equation*}
\frac{d}{dx}\left(\int_{0}^{x} \! f(t)\, dt\right)= \frac{d}{dx}\left(\int_{x}^{1} \! t^2f(t) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C \right)
\end{equation*}

Como $f$ es continua para toda $x$, por el teorema fundamental del cálculo en su segunda forma tenemos que

\begin{equation*}
\frac{d}{dx} \left( \int_{0}^{x} \! f(t)\, dt \right)= f(x)
\end{equation*}

y

\begin{align*}
\frac{d}{dx} \left( \int_{x}^{1} \! t^2f(t)\, dt \right)&= – \frac{d}{dx} \left( \int_{1}^{x} \! t^2f(t)\, dt \right)\\&= -x^2f(x).
\end{align*}

Entonces, derivando ambos lados de la expresión original nos resulta la ecuación

\begin{equation*}
f(x)=-x^2f(x)+2x^{15}+2x^{17},
\end{equation*}

de la cual se obtiene

\begin{align*}
f(x) (x^2+1)&=2x^{15}+2x^{17}\\
&=2x^{15}(x^2+1)
\end{align*}

Así, tenemos que

\begin{equation*}
f(x)=2x^{15}.
\end{equation*}

Sustituyendo $f(t)=2t^{15}$ en la ecuación (1), tenemos que

\begin{equation*}
\int_{0}^{x} \! 2t^{15}\, dt= \int_{x}^{1} \! t^2(2t^{15}) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C
\end{equation*}

Así,

\begin{align*}
\int_{0}^{x} \! 2t^{15}\, dt&= \int_{x}^{1} \! t^2(2t^{15}) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\int_{0}^{x} \! 2t^{15}\, dt &= -\int_{1}^{x} \! 2t^{17} \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\left. \frac{2t^{16}}{16} \right|_{0}^{x} &= – \left. \left(\frac{2t^{18}}{18} \right) \right|_{1}^{x}+\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\frac{x^{16}}{8} &= – \left( \frac{x^{18}}{9}-\frac{1}{9}\right)+\frac{x^{16}}{8}+\frac{x^{18}}{19}+C\\
\end{align*}

Con ello, tenemos que

\begin{equation*}
C+\frac{1}{9}=0.
\end{equation*}

Por lo tanto la función que satisface la ecuación es $f(x)=2x^{15}$ y el valor de la constante es $C= – \frac{1}{9}$.

$\square$

Más problemas

Hay más ejemplos de problemas relacionados con la aplicación del teorema fundamental del cálculo en la Sección 6.9 del libro Problem Solving through Problems de Loren Larson.

Trabajar hacia atrás

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasHay algunos laberintos en los cuales es más fácil empezar por la salida que por la entrada. Como que empezar al final nos da más información. De modo similar, hay algunos problemas que nos dan más información si empezamos por las conclusiones que por las hipótesis.

Así mismo, en algunos problemas se tiene que seguir un cierto proceso y la pregunta es acerca de algunos estados alcanzables. En vez de empezar con un estado y ver a dónde llega, es mejor preguntarse cómo pudimos llegar al estado buscado.

Estas ideas también sirven para saber «en donde estás» mientras resuelves un problema: ¿Qué es lo que quieres y qué es lo que sabes?

Ir a los videos…

Elegir notación efectiva

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasPara que las matemáticas realmente simplifiquen las cosas y no las compliquen más, una de las cosas que se necesita es tener una notación adecuada.

En esta serie de videos veremos algunos ejemplos en los cuales elegir variables adecuadas o una representación adecuada del problema puede ayudar en la solución del problema o bien simplifica algunas cuentas.

Ir a los videos…