Introducción
Estamos a punto de entrar a discutir dos de los resultados principales de nuestro curso: el teorema de la función inversa y el teorema de la función implícita. Repasemos un poco qué hemos hecho hasta ahora. En las dos entradas anteriores introdujimos la noción de diferenciabilidad, la cual cuando sucede para una función $f:\mathbb{R}^n\to \mathbb{R}^m$, nos dice que $f$ se parece mucho a una función lineal en un punto dado. Vimos que esta noción implica continuidad y que tiene una regla de la cadena relacionada con el producto de matrices. También, hemos discutido cómo esta noción se relaciona con la existencia de espacios tangentes a gráficas multidimensionales.
Ahora queremos entender todavía mejor a las funciones diferenciables. Hay dos teoremas que nos permiten hacer eso. Uno es el teorema de la función inversa y el otro es el teorema de la función implícita. En esta entrada hablaremos del primero, y en un par de entradas más introduciremos el segundo resultado. El propósito del teorema de la función inversa es dar una condición bajo la cual una función es invertible, por lo menos localmente. De hecho, la mayoría de las veces sólo se puede garantizar la invertibilidad localmente, pues las funciones usualmente no son inyectivas y esto da comportamientos globales más difíciles de manejar.
Enunciar el teorema y entenderlo requiere de cierto esfuerzo. Y demostrarlo todavía más. Por esta razón, en esta entrada nos enfocaremos sólo en dar el teorema y presentar herramientas preliminares que necesitaremos para hacer su demostración.
Enunciado del teorema de la función inversa
Supongamos que tenemos $f:\mathbb{R}^n\to \mathbb{R}^n$ y que es diferenciable en el punto $\bar{a}$. Entonces, $f$ se parece mucho a una función lineal en $\bar{a}$, más o menos $f(\bar{x})\approx f(\bar{a}) + T_{\bar{a}}(\bar{x}-\bar{a})$. Así, si $T_{\bar{a}}$ es invertible, suena a que «cerquita de $\bar{a}$» la función $f(\bar{x})$ debe de ser invertible. El teorema de la función inversa pone estas ideas de manera formal.
Teorema (de la función inversa). Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el abierto $S$. Si la matriz $Df(\bar{a})$ es invertible, entonces, existe $\delta >0$ tal que:
- $B_{\delta}(\bar{a})\subseteq S$ y $f$ es inyectiva en $B_{\delta}(\bar{a})$.
- $f^{-1}:f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es continua en $f(B_{\delta}(\bar{a}))$.
- $f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}$ es un conjunto abierto.
- $f^{-1}$ es de clase $C^{1}$ en $f(B_{\delta}(\bar{a}))$ y además, si $\bar{x}=f(\bar{v})\in f(B_{\delta}(\bar{a}))$, entonces, $Df^{-1}(\bar{x})=Df^{-1}(f(\bar{v}))=(Df(\bar{v}))^{-1}$.
Veamos qué nos dice de manera intuitiva cada una de las conclusiones del teorema.
- Tendremos una bola $B_\delta(\bar{a})$ dentro de la cual $f$ será inyectiva, y por lo tanto será biyectiva hacia su imagen. Así, $f$ restringida a esta bola será invertible. Es importante que sea una bola abierta, porque entonces sí tenemos toda una región «gordita» en donde pasa la invertibilidad (piensa que si fuera un cerrado, a lo mejor sólo es el punto $\bar{a}$ y esto no tiene chiste).
- La inversa $f^{-1}$ que existirá para $f$ será continua. Esto es lo mínimo que podríamos esperar, aunque de hecho el punto $4$ garantiza algo mucho mejor.
- La imagen de $f$ en la bola $B_\delta(\bar{a})$ será un conjunto abierto.
- Más aún, se tendrá que $f^{-1}$ será de clase $C^1$ y se podrá dar de manera explícita a su derivada en términos de la derivada de $f$ con una regla muy sencilla: simplemente la matriz que funciona para derivar $f$ le sacamos su inversa como matriz y esa funciona al evaluarla en el punto apropiado.
El teorema de la función inversa es profundo pues tanto su enunciado como su demostración combina ideas de topología, álgebra y cálculo. Por esta razón, para su demostración necesitaremos recopilar varias de las herramientas de álgebra lineal que hemos repasado en la Unidad 2 y la Unidad 5. Así mismo, necesitaremos ideas topológicas de las que hemos visto en la Unidad 3. Con ellas desarrollaremos algunos resultados auxiliares que en la siguiente entrada nos permitirán concluir la demostración.
Un criterio para campos vectoriales $C^1$
El teorema de la función inversa es para funciones de clase $C^1$. Nos conviene entender esta noción mejor. Cuando una función $f$ es de clase $C^1$, entonces es diferenciable. Pero el regreso no es cierto y hay contraejemplos. ¿Qué le falta a una función diferenciable para ser de clase $C^1$? A grandes rasgos, que las funciones derivadas $T_\bar{a}$ y $T_\bar{b}$ hagan casi lo mismo cuando $\bar{a}$ y $\bar{b}$ son cercanos. En términos de matrices, necesitaremos que la expresión $||(Df(\bar{a})-Df(\bar{b}))(\bar{x})||$ sea pequeña cuando $\bar{a}$ y $\bar{b}$ son cercanos entre sí.
El siguiente teorema será importante en nuestro camino hacia el teorema de la función inversa. Intuitivamente, para lo que lo usaremos es para aproximar una función $f$ localmente, con «cuadritos» que corresponden a los planos tangentes, porque «muy cerquita» estos planos varían muy poco si pedimos que $f$ sea de clase $C^1$. Es decir si $\bar{a}$ y $\bar{b}$ son dos puntos en el dominio de una función diferenciable, y estos están muy cerca uno del otro, sus planos tangentes serán casi el mismo. Esto nos invita a cambiar localmente a una superficie por cuadritos como más adelante se explicará con detalle.
El teorema concreto que nos interesa demostrar es la siguiente equivalencia para que una función sea de clase $C^1$.
Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ una función diferenciable en $S$. Se tiene que $f$ es de clase $C^{1}$ en $S$ si y sólo si para todo $\bar{a}\in S$ y para cada $\varepsilon >0$ existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y si $\bar{b}\in B_{\delta}(\bar{a})$ se tiene $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq \varepsilon ||\bar{x}||$ para todo $\bar{x}\in \mathbb{R}^{n}$.
Demostración. $\Rightarrow).$ Supongamos que $f$ es de clase $C^1$ en $S$, es decir, todas sus funciones componentes tienen derivadas parciales en $S$ y son continuas. Sea $\varepsilon>0$. Veremos que se puede encontrar una $\delta$ como en el enunciado.
Tomemos $\bar{a}$ y $\bar{b}$ en $S$. Expresamos a $(Df(\bar{b})-Df(\bar{a}))(\bar{x})$ como
\begin{align*}
\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \dots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} x_{1} \\ \vdots \\ x_{n}\end{pmatrix}
\end{align*}
o equivalentemente como
\begin{align*}
\begin{pmatrix} \left( \triangledown f_{1}(\bar{b})-\triangledown f_{1}(\bar{a})\right) \cdot \bar{x} \\ \vdots \\ \left( \triangledown f_{m}(\bar{b})-\triangledown f_{m}(\bar{a})\right) \cdot \bar{x} \end{pmatrix}.
\end{align*}
De tal manera que por Cauchy-Schwarz:
\begin{align*}
||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2&=\sum_{i=1}^m (\left( \triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})\right)\cdot \bar{x})^2\\
&\leq \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2||\bar{x}||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m \sum_{j=1}^{n}\left( \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a})\right) ^{2}
\end{align*}
En este punto se ve la importancia de que las parciales sean continuas. Podemos encontrar una $\delta$ que nos garantice que $B_\delta\subseteq S$ y que si $||\bar{b}-\bar{a}||<\delta$, entonces $$\left| \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a}) \right| < \frac{\varepsilon}{\sqrt{mn}}.$$ En esta situación, podemos seguir acotando $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2$ como sigue:
\begin{align*}
&\leq ||\bar{x}|| \sum_{i=1}^m \sum_{j=1}^{n}\frac{\varepsilon^2}{mn}\\
&=\varepsilon^2||\bar{x}||^2.
\end{align*}
Al sacar raiz cuadrada, obtenemos la desigualdad $$||(Df(\bar{b})-Df(\bar{a}))(x)||\leq \varepsilon||\bar{x}||$$ buscada.
$\Leftarrow).$ Supongamos ahora que para cada $\varepsilon$ existe una $\delta$ como en el enunciado del teorema. Debemos ver que todas las derivadas parciales de todas las componentes son continuas. Podemos aplicar la desigualdad $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq ||\bar{x}||\varepsilon$ tomando como $\bar{x}$ cada vector $\hat{e}_i$ de la base canónica. Esto nos dice que
\[ ||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||< \varepsilon||\hat{e}_i|| =\varepsilon.\]
Por nuestro desarrollo anterior, para cada $i$ tenemos
\begin{align*}
\varepsilon&>||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||\\
&=||\left( \triangledown f_{1}(\bar{b})\cdot \hat{e}_i-\triangledown f_{1}(\bar{a})\cdot \hat{e}_i,\dots ,\triangledown f_{m}(\bar{b})\cdot \hat{e}_i-\triangledown f_{m}(\bar{a})\cdot \hat{e}_i\right)||\\
&=\left| \left|\left( \frac{\partial f_{1}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{i}}(\bar{a}),\dots ,\frac{\partial f_{m}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{i}}(\bar{a})\right) \right| \right|\\
&= \sqrt{\sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right)^{2}}.
\end{align*}
Elevando al cuadrado,
\[ \sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(b)-\frac{\partial f_{j}}{\partial x_{i}}(a)\right)^{2}<\varepsilon ^{2}.\]
Como todos los términos son no negativos, cada uno es menor a $\epsilon^2$. Así, para cada $i,j$ tenemos
\[ \left|\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right|<\varepsilon.\]
Esto es precisamente lo que estábamos buscando: si $\bar{b}$ está lo suficientemente cerca de $\bar{a}$, cada derivada parcial en $\bar{b}$ está cerca de su correspondiente en $\bar{a}$.
$\square$
Invertibilidad de $Df(\bar{a})$ en todo un abierto
En esta sección demostraremos lo siguiente. Si $f:\mathbb{R}^n\to \mathbb{R}^n$ es un campo vectorial diferenciable en $\bar{a}$ y $Df(\bar{a})$ es invertible, entonces $Df(\bar{x})$ será invertible para cualquier $\bar{x}$ alrededor de cierta bola abierta alrededor de $\bar{a}$. Los argumentos en esta ocasión están un poco más relacionados con el álgebra lineal.
Será útil que recuerdes que una transformación lineal $T:\mathbb{R}^n \to \mathbb{R}^n$ es invertible si el único $\bar{x}\in \mathbb{R}^n$ tal que $T(\bar{x})=\bar{0}$ es $\bar{x}=\bar{0}$. El siguiente criterio es otra caracterización de invertibilidad en términos de lo que le hace $T$ a la norma de los vectores.
Teorema. Sea $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una transformación lineal. La transformación $T$ es invertible si y sólo si existe $\varepsilon >0$ tal que $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.
Demostración. $\left. \Rightarrow \right)$ Como $T$ es invertible, para todo $\bar{x}\neq \bar{0}$ sucede que $T(\bar{x})\neq \bar{0}$. En particular, esto sucede para todos los vectores en $S^{n-1}$ (recuerda que es la esfera de radio $1$ y dimensión $n-1$ centrada en $\bar{0}$). Esta esfera es compacta y consiste exactamente de los $\bar{x}\in \mathbb{R}^n$ de norma $1$.
Sabemos que las transformaciones lineales y la función norma son continuas. Por la compacidad de $S^{n-1}$, la expresión $||T(\bar{x})||$ tiene un mínimo digamos $\varepsilon$, que alcanza en $S^{n-1}$. Por el argumento del párrafo anterior, $\varepsilon>0$.
Tomemos ahora cualquier vector $\bar{x}\in \mathbb{R}^n$. Si $\bar{x}=\bar{0}$, entonces $$||T(\bar{0})||=||\bar{0}||=0\geq \varepsilon ||\bar{0}||.$$ Si $\bar{x}\neq \bar{0}$, el vector $\frac{\bar{x}}{||\bar{x}||}$ está en $S^{n-1}$, de modo que $$\left|\left|T\left(\frac{\bar{x}}{||\bar{x}||}\right)\right|\right| \geq \varepsilon.$$ Usando linealidad para sacar el factor $||\bar{x}||$ y despejando obtenemos $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||,$$ como estábamos buscando.
$\left. \Leftarrow \right)$ Este lado es más sencillo. Si existe dicha $\varepsilon >0$, entonces sucede que para $\bar{x}$ en $\mathbb{R}^n$, con $\bar{x}\neq \bar{0}$ tenemos $$||T(\bar{x})||\geq \varepsilon||\bar{x}||>0.$$ Por lo tanto, $T(\bar{x})\neq \bar{0}$ y así $T$ es invertible.
$\square$
Obtengamos una consecuencia del teorema de clasificación de la sección anterior que está muy relacionada con este resultado que acabamos de demostrar.
Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el conjunto abierto $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces existen $\delta >0$ y $m>0$ tales que $B_{\delta}(\bar{a})\subseteq S$ y $||Df(\bar{b})(\bar{x})||\geq m||\bar{x}||$, para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.
Demostración. Como $Df(\bar{a})$ es invertible, por el teorema que acabamos de demostrar existe $\varepsilon’>0$ tal que $$||Df(\bar{a})(\bar{x})||\geq \varepsilon’||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.
Por nuestra caracterización de funciones $C^1$, Ahora como $f\in C^{1}$ en $S$ (abierto) para $\varepsilon =\frac{\varepsilon’}{2}>0$, existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y $||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\leq \frac{\varepsilon’}{2}||\bar{x}||$ para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.
Por la desigualdad del triángulo, \[ ||Df(\bar{a})(\bar{x})-Df(\bar{b})(\bar{x})||+||Df(\bar{b})(\bar{x})||\geq ||Df(\bar{a})(\bar{x})||,\]
de donde
\begin{align*}
||Df(\bar{b})(\bar{x})||&\geq ||Df(\bar{a})(\bar{x})||-||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\\
&\geq \varepsilon’||\bar{x}||-\frac{\varepsilon’}{2}||\bar{x}||\\
&= \frac{\varepsilon’}{2} ||\bar{x}||.
\end{align*}
De esta manera, el resultado es cierto para la $\delta$ que dimos y para $m=\frac{\varepsilon’}{2}$.
$\square$
El siguiente corolario es consecuencia inmediata de lo discutido en esta sección y está escrito de acuerdo a la aplicación que haremos más adelante en la demostración del teorema de la función inversa.
Corolario. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una función de clase $C^{1}$ en $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces, existe $\delta > 0$ tal que $B_{\delta}(\bar{a})\subseteq S$ y $Df(\bar{b})$ es invertible para todo $\bar{b}\in B_{\delta}(\bar{a})$.
Queda como tarea moral responder por qué este corolario es consecuencia inmediata del teorema anterior.
Un poco de intuición geométrica
Dejamos esta entrada hasta aquí, la naturaleza densamente teórica de lo que estamos haciendo puede hacer pesadas las exposiciones. Lo que hasta aquí demostramos es que para un campo vectorial $C^1$ si su derivada en $\bar{a}$ es invertible, entonces lo es en toda una vecindad que tiene a $\bar{a}$. Imaginemos al pedacito de superficie $f(B_{\delta}(\bar{a}))$ cubierto con pequeños rectángulos. En cada punto, las imágenes de estos rectángulos están muy cerquita, casi pegados a la superficie. Esto nos garantizaría la invertibilidad de $f$ en esta vecindad.
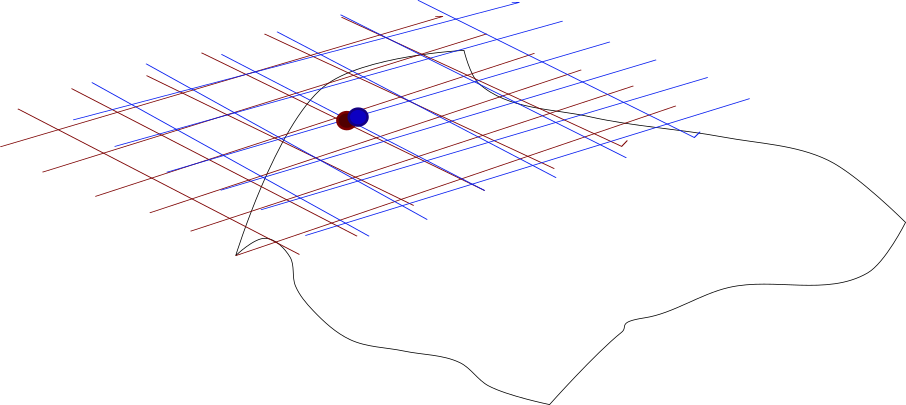
En la Figura 2 vemos ilustrado esto. El círculo inferior corresponde a la vecindad $B_{\delta}(\bar{a})$ en el dominio de $f$. La función $f$ levanta una porción del plano en la sabana delineada con negro arriba del círculo. En el círculo tenemos al punto $\bar{a}$ en verde agua. Sobre la sábana de arriba tenemos con el mismo color a $f(\bar{a})$. Los puntos negros pequeños dentro de la vecindad alrededor de $\bar{a}$ son alzados por $f$ a puntos negros sobre la sabana. Sobre de cada punto negro en la sabana tenemos un cuadrito rojo que representa al cachito de plano tangente cerca de la imagen de cada punto. La imagen esta llena de estos pequeños cuadritos, todos ellos representan diferenciales invertibles, esto nos permitirá asegurar la invertibilidad de $f$ en al menos una vecindad.
Más adelante…
En la siguiente entrada demostraremos el teorema de la función inversa, inciso por inciso. Es importante que estes familiarizado con los resultados de esta entrada, pues serán parte importante de la demostración.
Tarea moral
- ¿Qué diría el teorema de la función inversa para campos vectoriales $f:\mathbb{R}^2\to \mathbb{R}^2$? ¿Se puede usar para $$f(r,\theta)=(r\cos(\theta),r\sin(\theta))?$$ Si es así, ¿para qué valores de $r$ y $\theta$? ¿Qué diría en este caso explícitamente?
- Explica por qué el corolario que enunciamos en efecto se deduce de manera inmediata de lo discutido en la sección correspondiente.
- Revisa todas las desigualdades que usamos en esta entrada. ¿Qué resultado estamos usando? ¿Cuándo se darían estas igualdades?
- Demuestra que el determinante de una matriz es una función continua en términos de las entradas de la matriz. Usa esto para demostrar que si $A\in M_n(\mathbb{R})$ es una matriz y $B$ es una matriz muy cercana a $A$, entonces $B$ también es invertible.
- Demuestra que si una transformación $T$ es diagonalizable, entonces en el teorema de caracterización de invertibilidad se puede usar como $\epsilon$ al mínimo de la expresión $|\lambda|$ variando sobre todos los eigenvalores $\lambda$ de $T$.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral III
- Entrada anterior del curso: Regla de la cadena para campos vectoriales
- Entrada siguiente del curso: Demostración del teorema de la función inversa

