Archivo de la etiqueta: combinación lineal

Álgebra Lineal II: Existencia de la forma canónica de Jordan

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En las entradas anteriores demostramos que para cualquier matriz nilpotente existe (y es única) una matriz similar muy sencilla, hecha por lo que llamamos bloques de Jordan de eigenvalor cero. Lo que haremos ahora es mostrar una versión análoga de este resultado para una familia mucho más grande de matrices. De hecho, en cierto sentido tendremos un resultado análogo para todas las matrices.

Pensando en ello, lo que haremos en esta entrada es lo siguiente. Primero, generalizaremos nuestra noción de bloques de Jordan para contemplar cualquier eigenvalor. Estudiaremos un poco de los bloques de Jordan. Luego, enunciaremos el teorema que esperamos probar. Finalmente, daremos el primer paso hacia su demostración. En la siguiente entrada terminaremos la demostración y hablaremos de aspectos prácticos para encontrar formas canónicas de Jordan.

Enunciado del teorema de la forma canónica de Jordan

A continuación definimos a los bloques de Jordan para cualquier eigenvalor y tamaño.

Definición. Sea $F$ un campo. El bloque de Jordan de eigenvalor $\lambda$ y tamaño $k$ es la matriz $J_{\lambda,k}$ en $M_k(F)$ cuyas entradas son todas $\lambda$, a excepción de las que están inmediatamente arriba de la diagonal superior, las cuales son unos. En símbolos, $J_{\lambda,k}=[a_{ij}]$ con $$a_{ij}=\begin{cases} 1 & \text{si $j=i+1$}\\ \lambda & \text{si $i=j$} \\ 0 & \text{en otro caso.} \end{cases}$$

También podemos expresarlo de la siguiente manera:

$$J_{\lambda,k}=\begin{pmatrix} \lambda & 1 & 0 & \cdots & 0 & 0 \\ 0 & \lambda & 1 & \cdots & 0 & 0 \\ 0 & 0 & \lambda & \cdots & 0 & 0 \\ & \vdots & & \ddots & & \vdots \\ 0 & 0 & 0 & \cdots & \lambda & 1 \\ 0 & 0 & 0 & \cdots & 0 & \lambda \end{pmatrix},$$ en donde estamos pensando que la matriz es de $k\times k$.

Una última manera en la que nos convendrá pensar a $J_{\lambda,k}$ es en términos de los bloques de Jordan de eigenvalor cero: $J_{\lambda,k}=\lambda I_k + J_{0,k}$.

Definición. Una matriz de bloques de Jordan en $M_n(F)$ es una matriz diagonal por bloques en la que cada bloque en la diagonal es un bloque de Jordan.

Lo que nos gustaría demostrar es el siguiente resultado. En él, piensa en $\leq$ como algún orden total fijo de $F$ (para $\mathbb{R}$ es el orden usual, pero otros campos no necesariamente tienen un orden natural asociado).

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$ sobre el campo $F$ y $T:V\to V$ una transformación lineal tal que $\chi_T(X)$ se divide sobre $F$. Entonces, existen únicos valores $\lambda_1\leq \ldots \leq \lambda_n$ en $F$ y únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} para los cuales existe una base de $V$ en la cual $T$ tiene como forma matricial a la siguiente matriz de bloques de Jordan:

$$\begin{pmatrix} J_{\lambda_1,k_1} & 0 & \cdots & 0 \\ 0 & J_{\lambda_2,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{\lambda_d,k_d}\end{pmatrix}.$$

Por supuesto, este teorema también tiene una versión matricial, la cuál tendrás que pensar cómo escribir.

Un teorema de descomposición de kernels

Ya tenemos uno de los ingredientes que necesitamos para dar la demostración de la existencia de la forma canónica de Jordan: su existencia para las transformaciones nilpotentes. Otro de los ingredientes que usaremos es el teorema de Cayley-Hamilton. El tercer ingrediente es un resultado de descoposición de kernels de transformaciones evaluadas en polinomios.

Proposición. Sea $V$ un espacio vectorial sobre $F$. Sea $T:V\to V$ una transformación lineal. Y sean $P_1(X),\ldots,P_r(X)$ polinomios en $F[x]$ cuyo máximo común divisor de cualesquiera dos de ellos es el polinomio $1$. Entonces, $$\ker((P_1P_2\cdots P_r)(T))=\bigoplus_{i=1}^r \ker(P_i(T)).$$

Demostración. Para cada $i\in \{1,2,\ldots,r\}$ consideraremos a $Q_i(X)$ como el polinomio que se obtiene de multiplicar a todos los polinomios dados, excepto $P_i(X)$. Y por comodidad, escribiremos $P(X)=(P_1\cdots P_r)(X)$. Notemos que entonces $P(X)=(Q_iP_i)(X)$ para cualquier $i\in\{1,2,\ldots,r\}$.

Primero probaremos un resultado polinomial auxiliar. Veremos que $Q_1(X),\ldots,Q_r(X)$ tienen como máximo común divisor al polinomio $1$. En caso de no ser así, un polinomio $D(X)$ no constante dividiría a todos ellos. Sin pérdida de generalidad, $D$ es irreducible (tomando, por ejemplo $D(X)$ de grado mínimo con esta propiedad). Como $D(X)$ es irreducible y divide a $Q_r(X)$, entonces debe dividir a alguno de los factores de $Q_r(X)$, que sin pérdida de generalidad (por ejemplo, reetiquetando), es $P_1(X)$. Pero $D(X)$ también divide a $Q_1(X)$, así que debe dividir a alguno de sus factores $P_2(X),\ldots,P_r(X)$, sin pérdida de generalidad a $P_2(X)$. Pero entonces $D(X)$ divide a $P_1(X)$ y $P_2(X)$, lo cual contradice las hipótesis. Así, $Q_1(X),\ldots,Q_r(X)$ tienen como máximo común divisor al polinomio $1$. Por el lema de Bézout para polinomios (ver tarea moral), existen entonces polinomios $R_1(X),\ldots,R_r(X)$ tales que

\begin{equation}
\label{eq:bezout}(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(X)=1.
\end{equation}

Estamos listos para pasar a los argumentos de álgebra lineal. Veamos primero que cualquier elemento en la suma de la derecha está en el kernel de $P(T)$. Tomemos $v=v_1+\ldots+v_r$ con $v_i\in \ker(P_i(T))$. Al aplicar $P$ obtenemos

\begin{align*}
P(v)&=P(v_1)+\ldots+P(v_r)\\
&=Q_1(P_1(v_1))+\ldots+Q_r(P_r(v_r))\\
&=0+\ldots+0=0.
\end{align*}

Esto muestra que $v\in \ker(P(T))$, de donde se obtiene la primera contención que nos interesa.

Veamos ahora la segunda contención, que $\ker(P(T))=\bigoplus_{i=1}^r \ker(P_i(T))$. Tomemos $v\in \ker(P(T))$. Al aplicar \eqref{eq:bezout} en $T$ y evaluar en $v$ obtenemos que

\begin{align*}
v&=\text{Id}(v)=(1)(T)(v)\\
&=(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(T)(v)\\
&=(R_1Q_1)(T)(v)+\ldots+(R_rQ_r)(T)(v).
\end{align*}

Pero esto justo expresa a $v$ como elemento de $\ker(P_i(T))$ pues para cada $i$ tenemos

\begin{align*}
P_i(T)((R_iQ_i)(T)(v))&=(P_iR_i Q_i )(T)(v)\\
&=(R_i Q_i P_i)(T)(v)\\
&=R_i(T)P(T)(v)\\
&=R_i(0)=0,
\end{align*}

de modo que expresamos a $v$ como suma de vectores en $\ker(P_1(T)),\ldots,\ker(P_r(T))$.

Ya demostramos la igualdad de conjuntos, pero recordemos que en la igualdad de suma directa hay otra cosa que hay que probar: que el cero tiene una forma única de expresarse como suma de elementos de cada subespacio (aquella en donde cada elemento es cero). Supongamos entonces que $$0=v_1+\ldots+v_r$$ con $v_i\in \ker(P_i(T))$ para cada $i$. Si aplicamos $Q_i$ en esta igualdad, como tiene todos los factores $P_j$ con $j\neq i$ obtenemos $$0=Q_i(0)=Q_i(v_i).$$

Por otro lado, al aplicar nuevamente \eqref{eq:bezout} en $T$ y evaluar en $v_i$

\begin{align*}
v_i&=\text{Id}(v_i)=(1)(T)(v_i)\\
&=(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(T)(v_i)\\
&=(R_1Q_1)(T)(v_1)+\ldots+(R_rQ_r)(T)(v_i)\\
&=(R_iQ_i)(T)(v_i)\\
&=0.
\end{align*}

De esta forma, en efecto tenemos que los espacios están en posición de suma directa, que era lo último que nos faltaba verificar.

$\square$

Existencia de la forma canónica de Jordan

Estamos listos para demostrar la existencia de la forma canónica de Jordan. Supongamos que $V$ es un espacio vectorial de dimensión finita $n$ sobre $F$ y que $T:V\to V$ es una transformación lineal cuyo polinomio característico se divide en $F[x]$. Sabemos entonces que es de la siguiente forma:

$$\chi_T(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r},$$

donde $\lambda_1,\ldots,\lambda_r$ son eigenvalores distintos de $T$ y $m_1,\ldots,m_r$ son las multiplicidades algebraicas respectivas de estos eigenvalores como raíces de $\chi_T(X)$.

Por el teorema de Cayley-Hamilton, sabemos que $\chi_T(T)=0$, de modo que $\ker(\chi_T(T))=V$. Por la proposición de descomposición de la sección anterior aplicada a los polinomios $P_i(X)=(X-\lambda_i)^{m_i}$ (verifica que son primos relativos dos a dos) para $i\in\{1,\ldots,r\}$ tenemos entonces que $$V=\bigoplus_{i=1}^r \ker((T-\lambda_i \text{id})^{m_i}).$$

Pero, ¿cómo es la transformación $T-\lambda_i \text{id}$ restringida a cada $\ker((T-\lambda_i \text{id})^{m_i})$? ¡Es nilpotente! Precisamente por construcción, $(T-\lambda_i \text{id})^{m_i}$ se anula totalmente en este kernel. Así, por la existencia de la forma canónica de Jordan para matrices nilpotentes, hay una base $\beta_i$ para cada $\ker((T-\lambda_i \text{id})^{m_i})$ tal que $T-\lambda_i \text{id}$ restringida a ese kernel tiene como forma matricial una matriz $J_i$ de bloques de Jordan de eigenvalor cero. Pero entonces $T$ (restringida a dicho kernel) tiene como forma matricial a $J_i+\lambda_i I_{m_i}$, que es una matriz de bloques de Jordan de eigenvalor $\lambda$.

Con esto terminamos: como $V$ es la suma directa de todos esos kernel, la unión de bases $\beta_1,\ldots,\beta_r$ es una base para la cual $T$ tiene como forma matricial a una matriz de bloques de Jordan.

$\square$

Más adelante…

Hemos demostrado la existencia de la forma canónica de Jordan, pero aún nos falta demostrar su unicidad. Además de esto, también necesitaremos un mejor procedimiento para encontrarla. Haremos eso en la siguiente entrada.

Tarea moral

  1. Enuncia el teorema de la forma canónica de Jordan versión matrices.
  2. Investiga más sobre el lema de Bézout para polinomios y cómo se demuestra. Después de esto, expresa al polinomio $1$ como combinación lineal de los polinomios $x^2-1, x^3+1, x^2+5x+4$.
  3. Verifica que los polinomios $P_i(X)=(X-\lambda_i)^{k_i}$ de la demostración de la existencia de la forma canónica de Jordan cumplen las hipótesis de la proposición de descomposición de kernels.
  4. Sea $F$ un campo y $r,s$ elementos en $F$. Sea $n$ un entero. Demuestra que los bloques de Jordan $J_{r,n}$ y $J_{s,n}$ en $M_n(F)$ conmutan.
  5. Siguiendo las ideas de la demostración de existencia, encuentra la forma canónica de Jordan de la matriz $$\begin{pmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 2 \end{pmatrix}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Los espacios vectoriales $\mathbb{R}^2$ y $\mathbb{R}^3$

Por Eduardo García Caballero

Deja un comentario

Introducción

A lo largo de esta unidad nos hemos enfocado en estudiar los vectores, las operaciones entre estos y sus propiedades. Sin embargo, hasta ahora solo hemos ocupado una definición provisional de vectores —listas ordenadas con entradas reales—, pero no hemos dado una definición formal de estos. En esta entrada definiremos qué es un espacio vectorial y exploraremos algunas de las propiedades de dos ejemplos importantes de espacios vectoriales: $\mathbb{R}^2$ y $\mathbb{R}^3$-

Las propiedades de espacio vectorial

En entradas anteriores demostramos que los pares ordenados con entradas reales (es decir, los elementos de $\mathbb{R}^2$), en conjunto con la suma entrada a entrada y el producto escalar, cumplen las siguientes propiedades:

1. La suma es asociativa:
\begin{align*}
(u+v)+w &= ((u_1,u_2) + (v_1,v_2)) + (w_1,w_2) \\
&= (u_1,u_2) + ((v_1,v_2) + (w_1,w_2)) \\
&= u+(v+w).\end{align*}

2. La suma es conmutativa:
\begin{align*}u+v &= (u_1,u_2) + (v_1,v_2) \\&= (v_1,v_2) + (u_1,u_2) \\&= v+u.\end{align*}

3. Existe un elemento neutro para la suma:
\begin{align*}
u + 0 &= (u_1,u_2) + (0,0) \\&= (0,0) + (u_1,u_2) \\&= (u_1,u_2) \\&= u.
\end{align*}

4. Para cada par ordenado existe un elemento inverso:
\begin{align*}
u + (-u) &= (u_1,u_2) + (-u_1,-u_2) \\&= (-u_1,-u_2) + (u_1,u_2) \\&= (0,0) \\&= 0.
\end{align*}

5. La suma escalar se distribuye bajo el producto:
\begin{align*}
(r+s)u &= (r+s)(u_1,u_2) \\&= r(u_1,u_2) + s(u_1,u_2) \\&= ru + su.
\end{align*}

6. La suma de pares ordenados se distribuye bajo el producto escalar:
\begin{align*}
r(u + v) &= r((u_1,u_2) + (v_1,v_2)) \\&= r(u_1,u_2) + r(v_1,v_2) \\&= ru + rv.
\end{align*}

7. El producto escalar es compatible con el producto de reales:
\[
(rs)u = (rs)(u_1,u_2) = r(s(u_1,u_2)) = r(su).
\]

8. Existe un elemento neutro para el producto escalar, que justo es el neutro del producto de reales:
\[
1u = 1(u_1,u_2) = (u_1,u_2) = u.
\]

Cuando una colección de objetos matemáticos, en conjunto con una operación de suma y otra operación de producto, cumple las ocho propiedades anteriormente mencionadas, decimos que dicha colección forma un espacio vectorial. Teniendo esto en consideración, los objetos matemáticos que pertenecen a la colección que forma el espacio vectorial los llamaremos vectores.

Así, podemos ver que los pares ordenados con entradas reales, en conjunto con la suma entrada a entrada y el producto escalar, forman un espacio vectorial, al cual solemos denominar $\mathbb{R}^2$. De este modo, los vectores del espacio vectorial $\mathbb{R}^2$ son exactamente los pares ordenados con entradas reales.

Como recordarás, anteriormente también demostramos que las ternas ordenadas con entradas reales, en conjunto con su respectiva suma entrada a entrada y producto escalar, cumplen las ocho propiedades antes mencionadas (¿puedes verificarlo?). Esto nos indica que $\mathbb{R}^3$ también es un espacio vectorial, y sus vectores son las ternas ordenadas con entradas reales. En general, el que un objeto matemático se pueda considerar o no como vector dependerá de si este es elemento de un espacio vectorial.

Como seguramente sospecharás, para valores de $n$ distintos de 2 y de 3 también se cumple que $\mathbb{R}^n$ forma un espacio vectorial. Sin embargo los espacios $\mathbb{R}^2$ y $\mathbb{R}^3$ son muy importantes pues podemos visualizarlos como el plano y el espacio, logrando así describir muchas de sus propiedades. Por esta razón, en esta entrada exploraremos algunas de las principales propiedades de $\mathbb{R}^2$ y $\mathbb{R}^3$.

Observación. Basándonos en la definición, el hecho de que una colección de elementos se pueda considerar o no como espacio vectorial depende también a las operaciones de suma y producto. Por esta razón, es común (y probablemente más conveniente) encontrar denotado el espacio vectorial $\mathbb{R}^2$ como $(\mathbb{R}^2,+,\cdot)$. Más aún, a veces será importante destacar a los elementos escalares y neutros, encontrando el mismo espacio denotado como $(\mathbb{R}^2, \mathbb{R}, +, \cdot, 0, 1)$. Esto lo veremos de manera más frecuente cuando trabajamos con más de un espacio vectorial, sin embargo, cuando el contexto nos permite saber con qué operaciones (y elementos) se está trabajando, podemos omitir ser explícitos y denotar el espacio vectorial simplemente como $\mathbb{R}^2$ o $\mathbb{R}^3$.

Combinaciones lineales

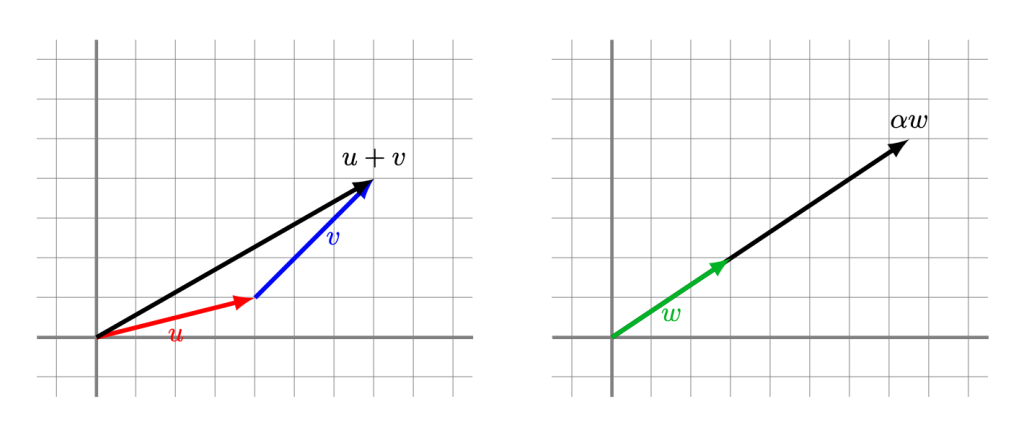
Como vimos en entradas anteriores, la suma de vectores en $\mathbb{R}^2$ la podemos visualizar en el plano como el resultado de poner una flecha seguida de otra, mientras que el producto escalar lo podemos ver como redimensionar y/o cambiar de dirección una flecha.

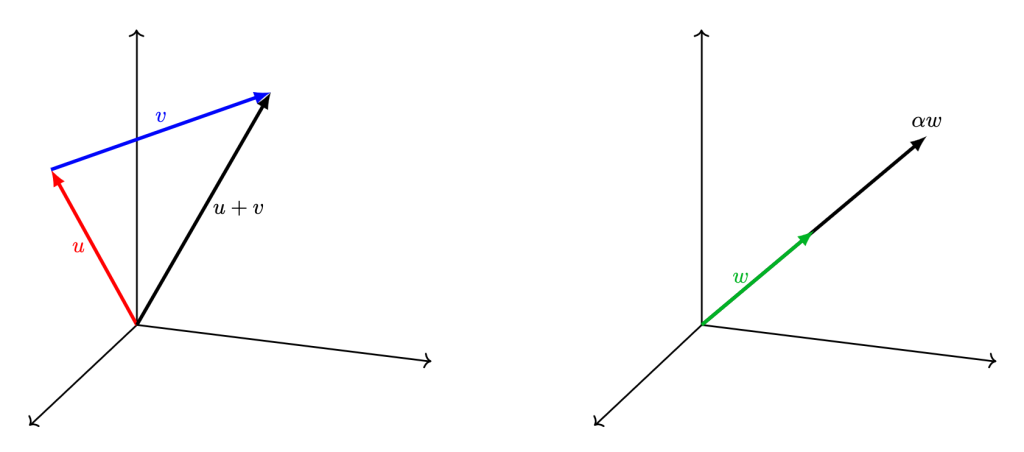
En el caso de $\mathbb{R}^3$, la intuición es la misma, pero esta vez en el espacio.

Si tenemos varios vectores, podemos sumar múltiplos escalares de ellos para obtener otros vectores. Esto nos lleva a la siguiente definición.

Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), definimos una combinación lineal de estos vectores como el resultado de la operación
\[
r_1v_1 + r_2v_2 + \cdots + r_nv_n,
\]
donde $r_1, \ldots, r_n$ son escalares.

Ejemplo. En $\mathbb{R}^2$, las siguientes son combinaciones lineales:
\begin{align*}
4(9,-5) + 7(-1,0) + 3(-4,2) &= (17,-14), \\[10pt]
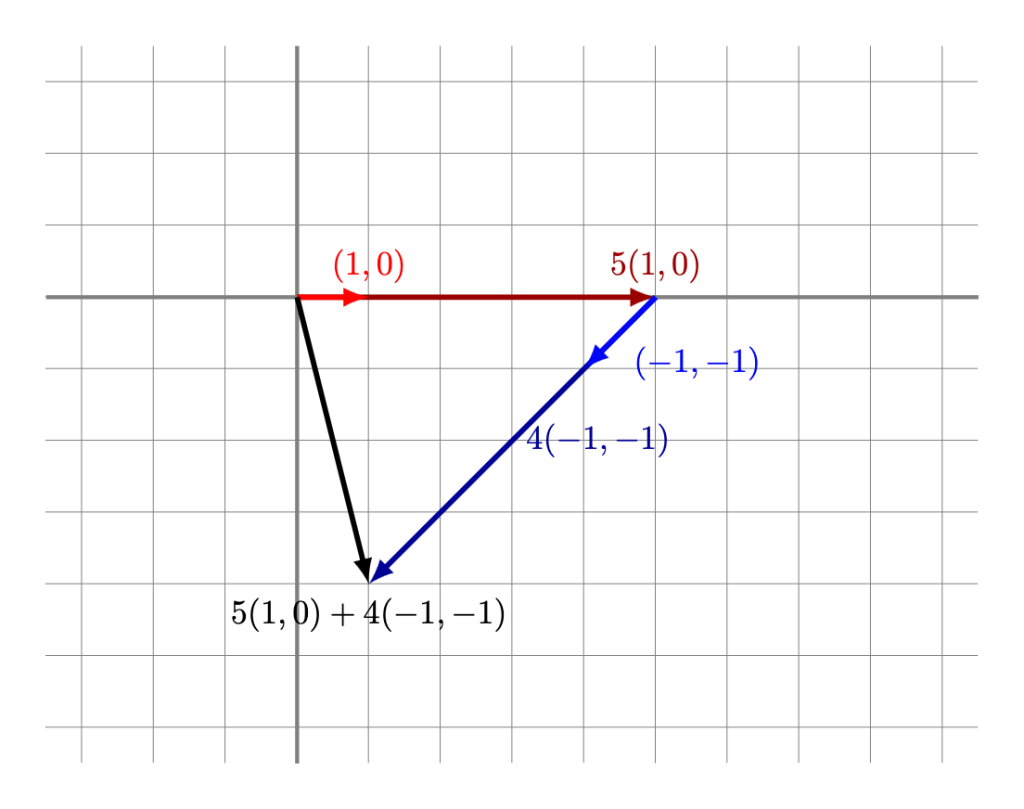
5(1,0) + 4(-1,-1) &= (1,-4), \\[10pt]
-1(1,0) + 0(-1,-1) &= (-1,0), \\[10pt]
5(3,2) &= (15,10).
\end{align*}
De este modo podemos decir que $(17,-14)$ es combinación lineal de los vectores $(9,-5)$, $(-1,0)$ y $(-4,2)$; los vectores $(1,-4)$ y $(-1,0)$ son ambos combinación lineal de los vectores $(1,0)$ y $(-1,-1)$; y $(15,10)$ es combinación lineal de $(3,2)$.

Las combinaciones lineales también tienen un significado geométrico. Por ejemplo, la siguiente figura muestra cómo se vería que $(1,-4)$ es combinación lineal de $(1,0)$ y $(-1,-1)$:

$\triangle$

Ejemplo. En el caso de $\mathbb{R}^3$, observamos que $(7,13,-22)$ es combinación lineal de los vectores $(8,1,-5)$, $(1,0,2)$ y $(9,-3,2)$, pues
\[
4(8,1,-5) + 2(1,0,2) + (-3)(9,-3,2) = (7,13,-22).
\]

$\triangle$

Espacio generado

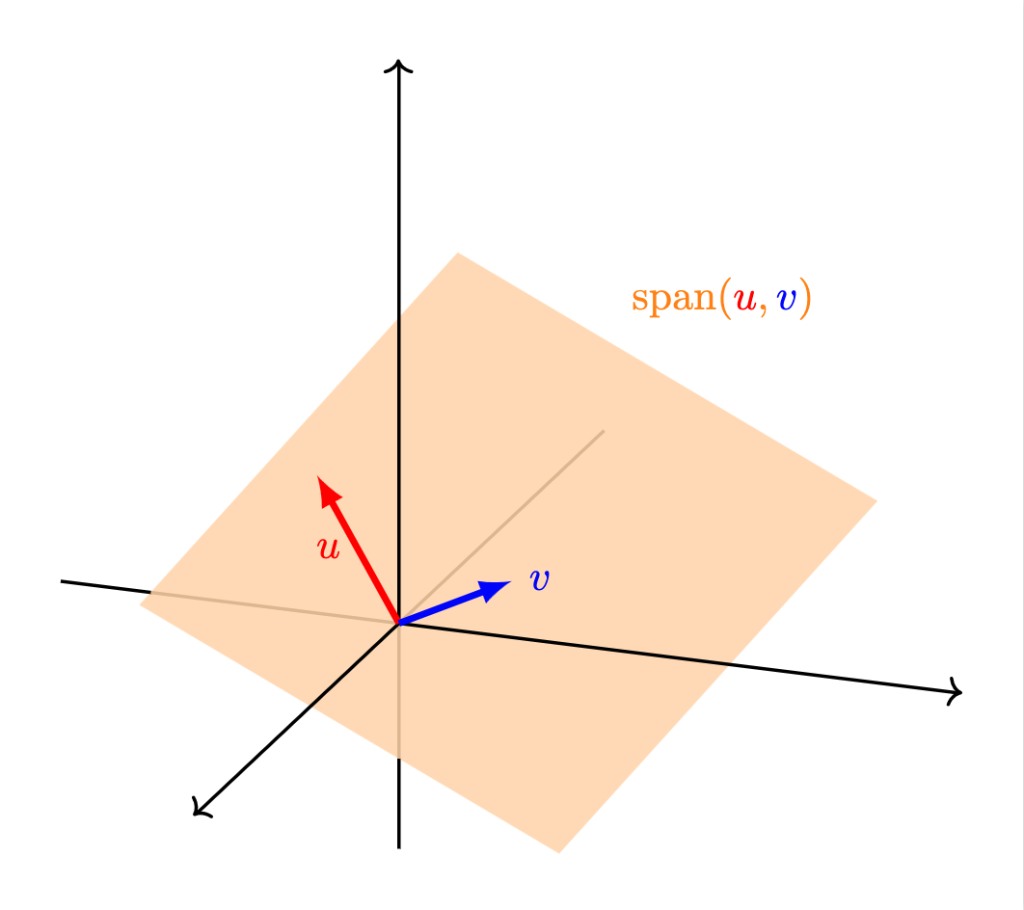
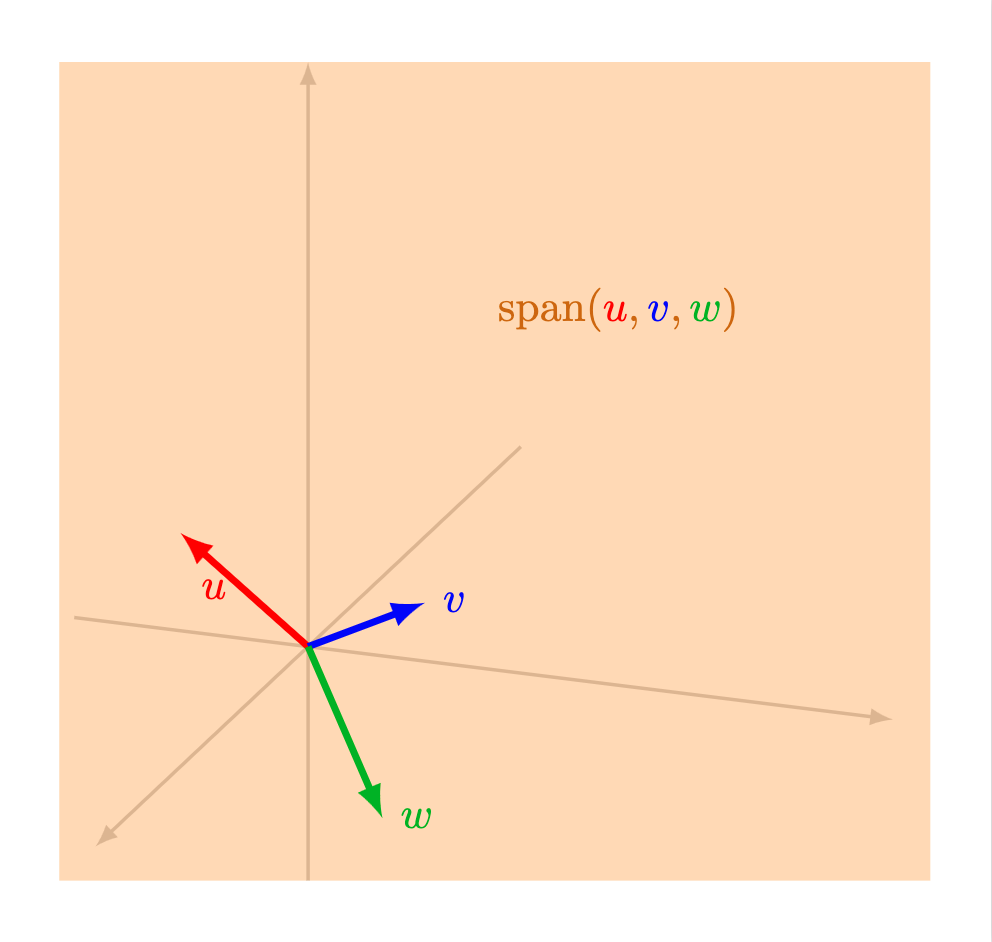
La figura de la sección anterior nos sugiere cómo entender a una combinación lineal de ciertos vectores dados. Sin embargo, una pregunta natural que surge de esto es cómo se ve la colección de todas las posibles combinaciones lineales de una colección de vectores dados.

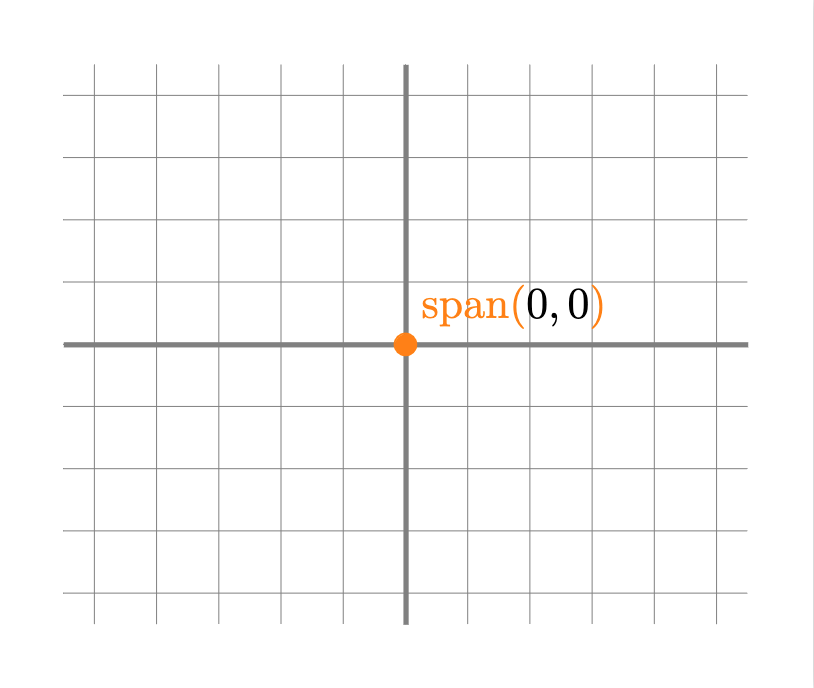
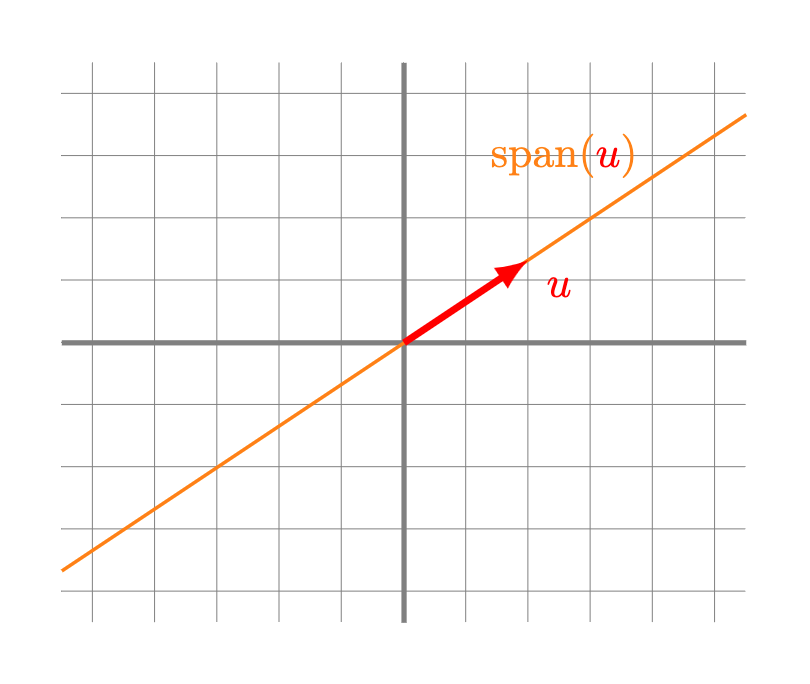
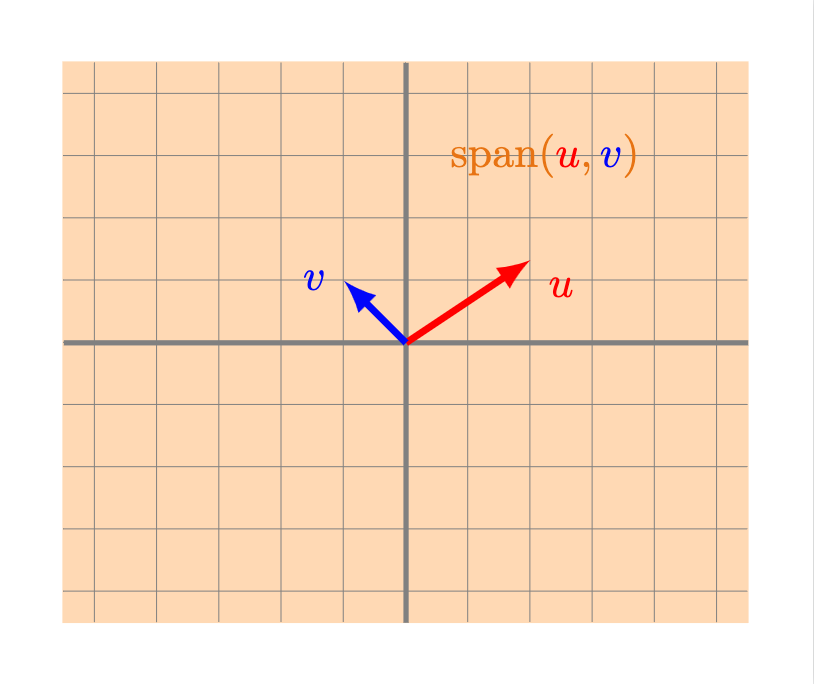
Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), definimos al espacio generado por ellos como el conjunto de todas sus posibles combinaciones lineales. Al espacio generado por estos vectores podemos encontrarlo denotado como $\operatorname{span}(v_1, \ldots, v_n)$ o $\langle v_1, \ldots, v_n \rangle$ (aunque esta última notación a veces se suele dejar para otra operación del álgebra lineal).

¿Cómo puede verse el espacio generado por algunos vectores? Puede demostrarse que en el caso de $\mathbb{R}^2$ tenemos los siguientes casos.

  • Un punto: esto sucede si y sólo si todos los vectores del conjunto son iguales al vector $0$.
  • Una recta: esto sucede si al menos un vector $u$ es distinto de 0 y todos los vectores se encuentran alineados. La recta será precisamente aquella formada por los múltiplos escalares de $u$.
  • Todo $\mathbb{R}^2$: esto sucede si al menos dos vectores $u$ y $v$ de nuestro conjunto no son cero y además no están alineados. Intenta convencerte que en efecto en este caso puedes llegar a cualquier vector del plano sumando un múltiplo de $u$ y uno de $v$.

En $\mathbb{R}^3$, puede mostrarse que el espacio generado se ve como alguna de las siguientes posibilidades:

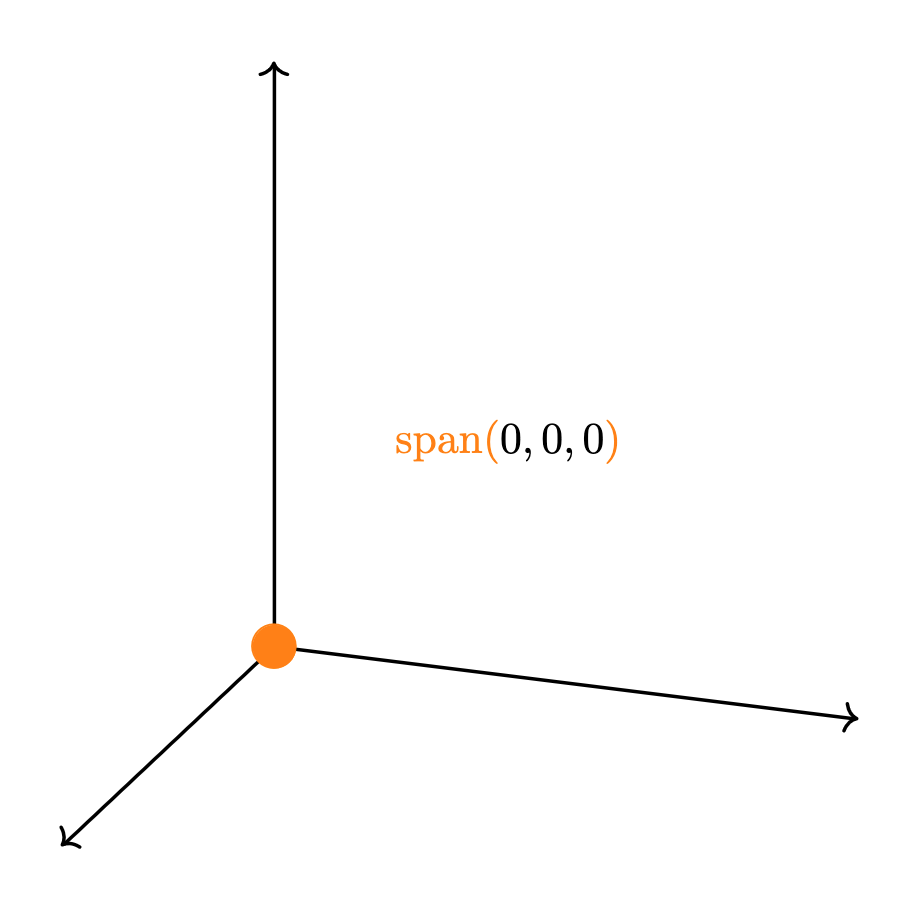
  • Un punto: esto sucede si y sólo si todos los vectores del conjunto son iguales al vector $0$.
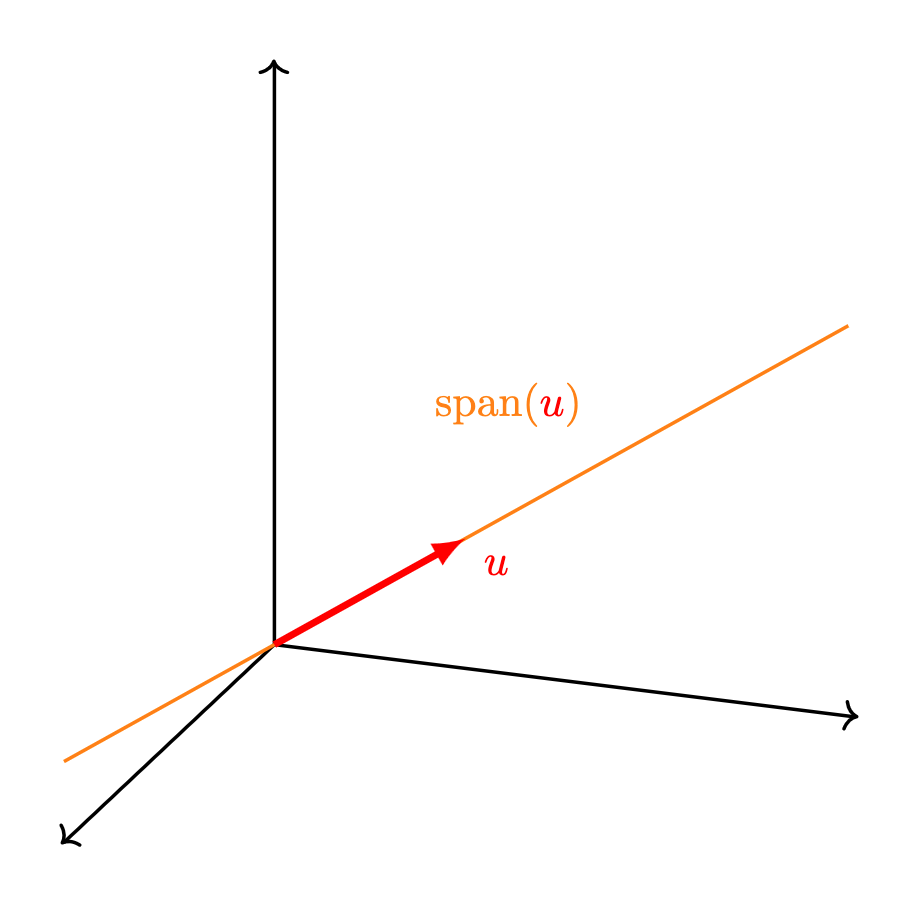
  • Una recta: esto sucede si al menos un vector $u$ es distinto de $0$ y todos los vectores se encuentran alineados con $u$. La recta consiste precisamente de los reescalamientos de $u$.
  • Un plano: esto sucede si al menos dos vectores $u$ y $v$ no son cero y no están alineados, y además todos los demás están en el plano generado por $u$ y $v$ estos dos vectores.
  • Todo $\mathbb{R}^3$: esto sucede si hay tres vectores $u$, $v$ y $w$ que cumplan que ninguno es el vector cero, no hay dos de ellos alineados, y además el tercero no está en el plano generado por los otros dos.

Muchas veces no sólo nos interesa conocer la forma del espacio generado, sino también obtener una expresión que nos permita conocer qué vectores pertenecen a este. Una forma en la que podemos hacer esto es mediante ecuaciones.

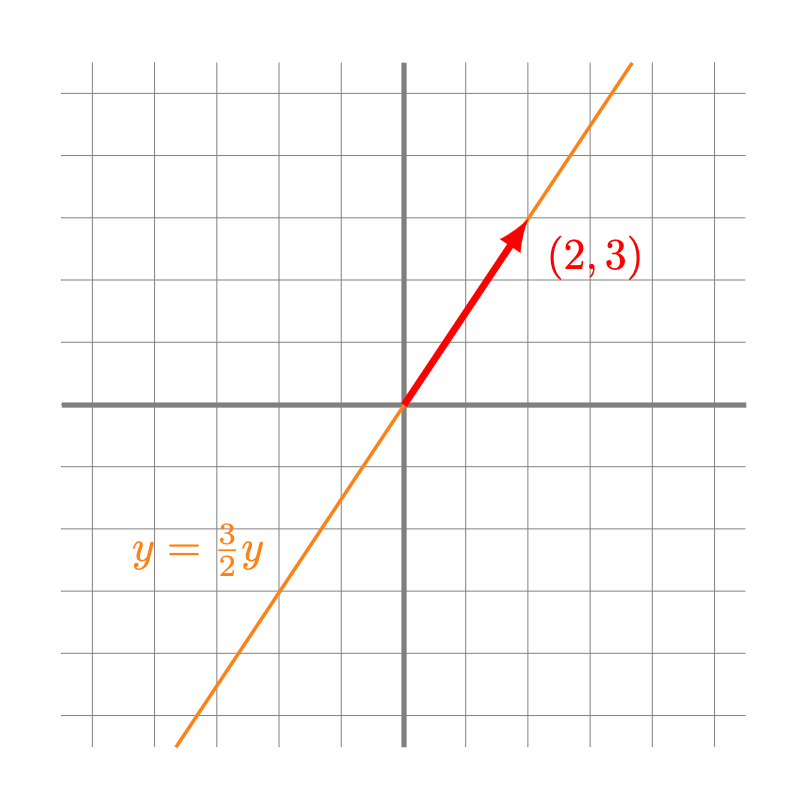
Ejemplo. Por ejemplo, observemos que el espacio generado el vector $(3,2)$ en $\mathbb{R}^2$ corresponde a los vectores $(x,y)$ que son de la forma
\[
(x,y) = r(2,3),
\]
donde $r \in \mathbb{R}$ es algún escalar. Esto se cumple si y sólo si
\[
(x,y) = (2r,3r),
\]
lo cual a su vez se cumple si y sólo si $x$ y $y$ satisfacen el sistema de ecuaciones
\[
\begin{cases}
x = 2r \\
y = 3r
\end{cases}.
\]
Si despejamos $r$ en ambas ecuaciones y las igualamos, llegamos a que
\[
\frac{x}{2} = \frac{y}{3},
\]
de donde podemos expresar la ecuación de la recta en su forma homogénea:
\[
\frac{1}{2}x – \frac{1}{3}y = 0;
\]
o bien en como función de $y$:
\[
y = \frac{3}{2}x.
\]

$\triangle$

La estrategia anterior no funciona para todos los casos, y tenemos que ser un poco más cuidadosos.

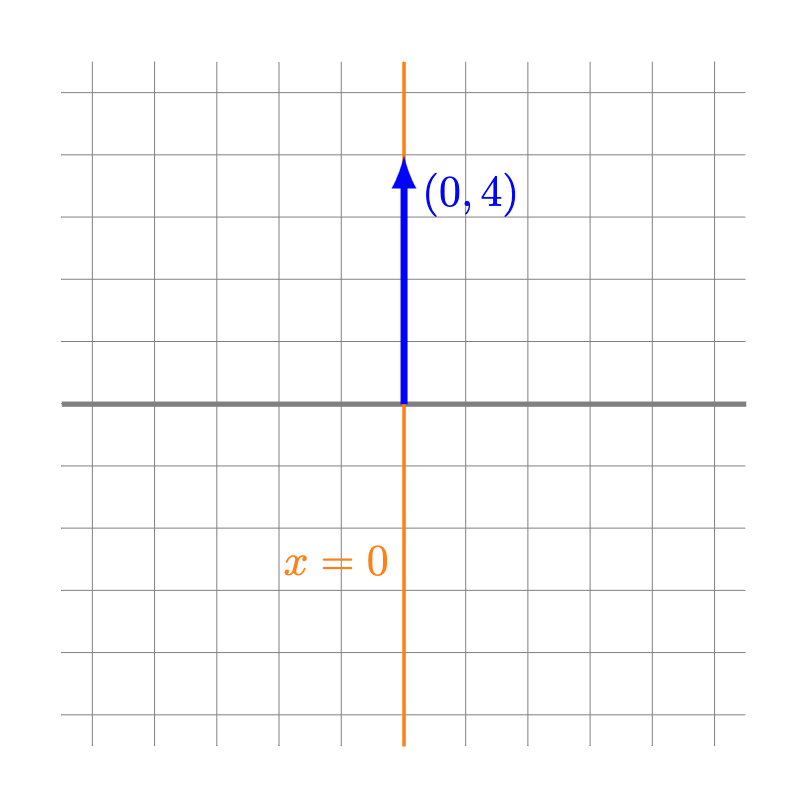
Ejemplo. El espacio generado por $(0,4)$ corresponde a todos los vectores $(x,y)$ tales que existe $r \in \mathbb{R}$ que cumple
\begin{align*}
(x,y) &= r(0,4) \\
(x,y) &= (0,4r),
\end{align*}
es decir,
\[
\begin{cases}
x = 0 \\
y = 4r
\end{cases}.
\]
En este caso, la única recta que satisface ambas ecuaciones es la recta $x = 0$, la cual no podemos expresar como función de $y$.

En la siguiente entrada veremos otras estrategias para describir de manera analítica el espacio generado.

$\triangle$

El saber si un vector está o no en el espacio generado por otros es una pregunta que se puede resolver con un sistema de ecuaciones lineales.

Ejemplo. ¿Será que el vector $(4,1,2)$ está en el espacio generado por los vectores $(2,3,1)$ y $(1,1,1)$? Para que esto suceda, necesitamos que existan reales $r$ y $s$ tales que $r(2,3,1)+s(1,1,1)=(4,1,2)$. Haciendo las operaciones vectoriales, esto quiere decir que $(2r+s,3r+s,r+s)=(4,1,2)$, de donde tenemos el siguiente sistema de ecuaciones:

$$\left\{\begin{matrix} 2r+s &=4 \\ 3r+s&=1 \\ r+s &= 2.\end{matrix}\right.$$

Este sistema no tiene solución. Veamos por qué. Restando la primera igualdad a la segunda, obtendríamos $r=1-4=-3$. Restando la tercera igualdad a la primera, obtendríamos $r=2-4=-2$. Así, si hubiera solución tendríamos la contradicción $-2=r=-3$. De este modo no hay solución.

Así, el vector $(4,1,2)$ no está en el espacio generado por los vectores $(2,3,1)$ y $(1,1,1)$. Geométricamente, $(4,1,2)$ no está en el plano en $\mathbb{R}^3$ generado por los vectores $(2,3,1)$ y $(1,1,1)$.

$\triangle$

Si las preguntas de espacio generado tienen que ver con sistemas de ecuaciones lineales, entonces seguramente estarás pensando que todo lo que hemos aprendido de sistemas de ecuaciones lineales nos servirá. Tienes toda la razón. Veamos un ejemplo importante.

Ejemplo. Mostraremos que cualquier vector en $\mathbb{R}^2$ está en el espacio generado por los vectores $(1,2)$ y $(3,-1)$. Para ello, tomemos el vector $(x,y)$ que nosotros querramos. Nos gustaría (fijando $x$ y $y$) poder encontrar reales $r$ y $s$ tales que $r(1,2)+s(3,-1)=(x,y)$. Esto se traduce al sistema de ecuaciones

$$\left \{ \begin{matrix} r+3s&=x\\2r-s&=y. \end{matrix} \right.$$

En forma matricial, este sistema es $$\begin{pmatrix} 1 & 3 \\ 2 & -1 \end{pmatrix} \begin{pmatrix} r \\ s \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix}.$$

Como la matriz $\begin{pmatrix} 1 & 3 \\ 2 & -1 \end{pmatrix}$ tiene determinante $1(-1)-(3)(2)=-7$, entonces es invertible. ¡Entonces el sistema siempre tiene solución única en $r$ y $s$ sin importar el valor de $x$ y $y$! Hemos con ello demostrado que cualquier vector $(x,y)$ es combinación lineal de $(1,2)$ y $(3,-1)$ y que entonces el espacio generado por ambos es todo $\mathbb{R}^2$.

$\triangle$

Independencia lineal

Mientras platicábamos en la sección anterior de las posibilidades que podía tener el espcio generado de un conjunto de vectores en $\mathbb{R}^2$ y $\mathbb{R}^3$, fuimos haciendo ciertas precisiones: «que ningún vector sea cero», «que nos vectores no estén alineados», «que ningún vector esté en los planos por los otros dos», etc. La intuición es que si pasaba lo contrario a alguna de estas cosas, entonces los vectores no podían generar «todo lo posible». Si sí se cumplían esas restricciones, entonces cierta cantidad de vectores sí tenía un espacio generado de la dimensión correspondiente (por ejemplo, $2$ vectores de $\mathbb{R}^3$ no cero y no alineados sí generan un plano, algo de dimensión $2$). Resulta que todas estas restricciones se pueden resumir en una definición muy importante.

Definición. Dado un conjunto de $n$ vectores $v_1, \ldots, v_n$ en $\mathbb{R}^2$ o ($\mathbb{R}^3$), diremos que son linealmente independientes si es imposible escribir al vector $0$ como combinación lineal de ellos, a menos que todos los coeficientes de la combinación lineal sean iguales a $0$. En otras palabras, si sucede que $$r_1v_1 + r_2v_2 + \cdots + r_nv_n=0,$$ entonces forzosamente fue porque $r_1=r_2=\ldots=r_n=0$.

Puede mostrarse que si un conjunto de vectores es linealmente independiente, entonces ninguno de ellos se puede escribir como combinación lineal del resto de vectores en el conjunto. Así, la intuición de que «generan todo lo que pueden generar» se puede justificar como sigue: como el primero no es cero, genera una línea. Luego, como el segundo no es múltiplo del primero, entre los dos generarán un plano. Y si estamos en $\mathbb{R}^3$, un tercer vector quedará fuera de ese plano (por no ser combinación lineal de los anteriores) y entonces generarán entre los tres a todo el espacio.

La independencia lineal también se puede estudiar mediante sistemas de ecuaciones lineales.

Ejemplo. ¿Serán los vectores $(3,-1,-1)$, $(4,2,1)$ y $(0,-10,-7)$ linealmente independientes? Para determinar esto, queremos saber si existen escalares $r,s,t$ tales que $r(3,-1,-1)+s(4,2,1)+t(0,-10,-7)=(0,0,0)$ en donde al menos alguno de ellos no es el cero. Esto se traduce a entender las soluciones del siguiente sistema de ecuaciones:

$$\left\{ \begin{array} 33r + 4s &= 0 \\ -r +2s -10t &= 0 \\ -r + s -7t &= 0.\end{array} \right. $$

Podemos entender todas las soluciones usando reducción Gaussiana en la siguiente matriz:

$$\begin{pmatrix} 3 & 4 & 0 & 0 \\ -1 & 2 & -10 & 0 \\ -1 & 1 & -7 & 0 \end{pmatrix}.$$

Tras hacer esto, obtenemos la siguiente matriz:

$$\begin{pmatrix}1 & 0 & 4 & 0\\0 & 1 & -3 & 0\\0 & 0 & 0 & 0 \end{pmatrix}.$$

Así, este sistema de ecuaciones tiene a $t$ como variable libre, que puede valer lo que sea. De aquí, $s=3t$ y $r=-4t$ nos dan una solución. Así, este sistema tiene una infinidad de soluciones. Tomando por ejemplo $t=1$, tenemos $s=3$ y $r=-4$. Entonces hemos encontrado una combinación lineal de los vectores que nos da el vector $(0,0,0)$. Puedes verificar que, en efecto, $$(-4)(3,-1,-1)+3(4,2,1)+(0,-10,-7)=(0,0,0).$$

Concluimos que los vectores no son linealmente independientes.

$\triangle$

Si la única solución que hubiéramos obtenido es la $r=s=t=0$, entonces la conclusión hubiera sido que sí, que los vectores son linealmente independientes. También podemos usar lo que hemos aprendido de matrices y determinantes en algunos casos para poder decir cosas sobre la independencia lineal.

Ejemplo. Mostraremos que los vectores $(2,3,1)$, $(0,5,2)$ y $(0,0,1)$ son linealmente independientes. ¿Qué sucede si una combinación lineal de ellos fuera el vector cero? Tendríamos que $r(2,3,1)+s(0,5,2)+t(0,0,1)=(0,0,0)$, que se traduce en el sistema de ecuaciones $$\left\{ \begin{array} 2r &= 0 \\ 3r + 5s &= 0 \\ r + 2s + t &= 0. \end{array}\right.$$

La matriz asociada a este sistema de ecuaciones es $\begin{pmatrix} 2 & 0 & 0 \\ 3 & 5 & 0 \\ 1 & 2 & 1 \end{pmatrix}$, que por ser triangular inferior tiene determinante $2\cdot 5 \cdot 1 = 10\neq 0$. Así, es una matriz invertible, de modo que el sistema de ecuaciones tiene una única solución. Como $r=s=t$ sí es una solución, esta debe ser la única posible. Así, los vectores $(2,3,1)$, $(0,5,2)$ y $(0,0,1)$ son linealmente independientes. Geométricamente, ninguno de ellos está en el plano hecho por los otros dos.

$\triangle$

Bases

Como vimos anteriormente, existen casos en los que el espacio generado por vectores en $\mathbb{R}^2$ (o $\mathbb{R}^3$) no genera a todo el plano (o al espacio). Por ejemplo, en ambos espacios vectoriales, el espacio generado por únicamente un vector es una recta. Esto también puede pasar aunque tengamos muchos vectores. Si todos ellos están alineados con el vector $0$, entonces su espacio generado sigue siendo una recta también. En la sección anterior platicamos que intuitivamente el problema es que los vectores no son linealmente independientes. Así, a veces unos vectores no generan todo el espacio que pueden generar.

Hay otras ocasiones en las que unos vectores sí generan todo el espacio que pueden generar, pero lo hacen de «manera redundante», en el sentido de que uno o más vectores se pueden poner de más de una forma como combinación lineal de los vectores dados.

Ejemplo. Si consideramos los vectores $(2,1)$, $(1,0)$ y $(2,3)$, observamos que el vector $(2,3)$ se puede escribir como
\[
0(2,1)+3(1,0) + 2(2,3) = (7,6)
\]
o
\[
3(2,2) + 1(1,0) + 0(2,3)= (7,6),
\]
siendo ambas combinaciones lineales del mismo conjunto de vectores.

$\triangle$

Uno de los tipos de conjuntos de vectores más importantes en el álgebra lineal son aquellos conocidos como bases, que evitan los dos problemas de arriba. Por un lado, sí generan a todo el espacio. Por otro lado, lo hacen sin tener redundancias.

Definición. Diremos que un conjunto de vectores es base de $\mathbb{R}^2$ (resp. $\mathbb{R}^3$) si su espacio generado es todo $\mathbb{R}^2$ (resp. $\mathbb{R}^3$) y además son linealmente independientes.

El ejemplo de base más inmediato es el conocido como base canónica.

Ejemplo. En el caso de $\mathbb{R}^2$, la base canónica es $(1,0)$ y $(0,1)$. En \mathbb{R}^3$ la base canónica es $(1,0,0)$, $(0,1,0)$ y $(0,0,1)$.

Partiendo de las definiciones dadas anteriormente, vamos que cualquier vector $(a,b)$ en $\mathbb{R}$ se puede escribir como $a(1,0) + b(0,1)$; y cualquier vector $(a,b,c)$ en $\mathbb{R}^3$ se puede escribir como $a(1,0,0) + b(0,1,0) + c(0,0,1)$.

Más aún, es claro que los vectores $(1,0)$ y $(0,1)$ no están alineados con el origen. Y también es claro que $(1,0,0),(0,1,0),(0,0,1)$ son linealmente idependientes, pues la combinación lineal $r(1,0,0)+s(0,1,0)+t(0,0,1)=(0,0,0)$ implica directamente $r=s=t=0$.

$\triangle$

Veamos otros ejemplos.

Ejemplo. Se tiene lo siguiente:

  • Los vectores $(3,4)$ y $(-2,0)$ son base de $\mathbb{R}^2$ pues son linealmente independientes y su espacio generado es todo $\mathbb{R}^2$.
  • Los vectores $(8,5,-1)$, $(2,2,7)$ y $(-1,0,9)$ son base de $\mathbb{R}^3$ pues son linealmente independientes y su espacio generado es todo $\mathbb{R}^3$.

¡Ya tienes todo lo necesario para demostrar las afirmaciones anteriores! Inténtalo y haz dibujos en $\mathbb{R}^2$ y $\mathbb{R}^3$ de dónde se encuentran estos vectores.

$\triangle$

Como podemos observar, las bases de un espacio vectorial no son únicas, sin embargo, las bases que mencionamos para $\mathbb{R}^2$ coinciden en tener dos vectores, mientras que las bases para $\mathbb{R}^3$ coinciden en tener tres vectores. ¿Será cierto que todas las bases para un mismo espacio vectorial tienen la misma cantidad de vectores?

Más adelante…

En esta entrada revisamos qué propiedades debe cumplir una colección de objetos matemáticos para que sea considerado un espacio vectorial, además de que analizamos con más detalle los espacios vectoriales $\mathbb{R}^2$ y $\mathbb{R}^3$.

Como seguramente sospecharás, para otros valores de $n$ también se cumple que $\mathbb{R}^n$, en conjunto con sus respectivas suma entrada a entrada y producto escalar, forman un espacio vectorial. Sin embargo, en contraste con los espacios $\mathbb{R}^2$ y $\mathbb{R}^3$, este espacio es más difícil de visualizar. En la siguiente entrada generalizaremos para $\mathbb{R}^n$ varias de las propiedades que aprendimos en esta entrada.

Tarea moral

  1. Realiza lo siguiente:
    • De entre los siguientes vectores, encuentra dos que sean linealmente independientes: $(10,16),(-5,-8),(24,15),(10,16),(15,24),(-20,-32)$.
    • Encuentra un vector de $\mathbb{R}^2$ que genere a la recta $2x+3y=0$.
    • Determina qué es el espacio generado por los vectores $(1,2,3)$ y $(3,2,1)$ de $\mathbb{R}^3$.
    • Da un vector $(x,y,z)$ tal que $(4,0,1)$, $(2,1,0)$ y $(x,y,z)$ sean una base de $\mathbb{R}^3$.
  2. Demuestra que $(0,0)$ es el único vector $w$ en $\mathbb{R}^2$ tal que para todo vector $v$ de $\mathbb{R}^2$ se cumple que $v+w=v=w+v$.
  3. Prueba las siguientes dos afirmaciones:
    • Tres o más vectores en $\mathbb{R}^2$ nunca son linealmente independientes.
    • Dos o menos vectores en $\mathbb{R}^3$ nunca son un conjunto generador.
  4. Sean $u$ y $v$ vectores en $\mathbb{R}^2$ distintos del vector cero. Demuestra que $u$ y $v$ son linealmente independientes si y sólo si $v$ no está en la línea generada por $u$.
  5. Encuentra todas las bases de $\mathbb{R}^3$ en donde las entradas de cada uno de los vectores de cada base sean iguales a $0$ ó a $1$.

Entradas relacionadas

Álgebra Superior II: Mínimo común múltiplo

Por Ana Ofelia Negrete Fernández

Deja un comentario

Introducción

En la entrada anterior hablamos del máximo común divisor, para lo cual lo definimos en términos de ideales. Luego vimos que cumplía las propiedades que esperábamos. Es el turno de hacer lo mismo con el mínimo común múltiplo.

Recordando lo que nos enseñaron en la educación básica, el mínimo común múltiplo de dos enteros $a$ y $b$ tenía que ser simultáneamente múltiplo de ambos y, a la vez, tenía que ser lo más pequeño posible. Siendo un poco más precisos, tenía que ser un múltiplo positivo.

Como ejemplo, tomemos $a = 6$, $b = 8$. Una manera muy sencilla de encontrar un múltiplo en común es multiplicando ambos: $6\cdot 8 = 48$. Pero este no es el múltiplo más pequeño. Para poder encontrar aquel que sí sea el más pequeño, podemos enlistar los múltiplos de cada uno de estos números:

  • Múltiplos de $6$: $6,12,18,24,30,36, \ldots$
  • Múltiplos de $8$: $8, 16, 24, 32, 40, \ldots$

Notamos que el número más pequeño que está en ambas listas es el $24$. En educación básica había otras maneras de obtener esto sin hacer las listas anteriores, por ejemplo, mediante la siguiente tabla, en donde «vamos encontrando divisores en común, o bien de cada número».

862
432
232
133
1
El mínimo común múltiplo de 8 y 6 es $2^3\cdot 3 = 24.$

Lo que haremos será un poco distinto. Nuestra definición se basará nuevamente en el concepto de ideales. Veremos cómo hacer esto y cómo regresar al terreno familiar de mínimo común múltiplo que ya conocemos.

Mínimo Común Múltiplo

En la entrada de ideales en $\mathbb{Z}$ demostramos que la intersección de cualesquiera dos ideales es un ideal. También vimos que cualquier ideal era generado por algún entero no negativo. Esto nos lleva a la siguiente definición.

Definición. Sean $a$ y $b$ números enteros. Definimos a su mínimo común múltiplo como al entero no negativo $k$ tal que $a\mathbb{Z} \cap b\mathbb{Z} = k \mathbb{Z}$. En símbolos, nos referimos al mínimo común múltiplo de $a$ y $b$ como $\text{mcm}(a,b)$, o bien simplemente como $[a,b]$.

Ejemplo. Retomemos el ejemplo de la introducción. Si queremos calcular, por definición, al mínimo común múltiplo de los enteros $6$ y $8$, debemos considerar a los ideales $6\mathbb{Z}$ y $8\mathbb{Z}$, que respectivamente son:

$$6 \mathbb{Z} = \{\ldots, -12, -6, 0, 6, 12 ,18, 24, \ldots \}$$

$$8 \mathbb{Z}= \{\ldots, -16, -8, 0 ,8, 16, 24, 32, \ldots \}$$

Si hacemos la intersección de ambos ideales, notemos que obtenemos lo siguiente:

$$6 \mathbb{Z} \cap 8 \mathbb{Z} = \{\ldots, -24, 0, 24, 48, 72, \ldots\},$$

que es el ideal generado por el $24$. Así, tenemos, por definición, que el mínimo común múltiplo de $6$ y $8$ es igual a $24$.

$\triangle$

Propiedad fundamental del mínimo común múltiplo

Lo que nos gustaría hacer ahora es demostrar que el mínimo común múltiplo que obtuvimos de nuestra definición es, en efecto, el número que cumple con las propiedades que esperamos. Escribimos esto en la siguiente proposición.

Proposición. Sean $a$ y $b$ números enteros. Se cumple que:

  • $a\mid [a,b]$ y $b\mid [a,b]$
  • Si $a\mid m$ y $b\mid m$, entonces $[a,b]\mid m$.

Demostración. La primera parte es sencilla. Como $[a,b]$ genera a $a\mathbb{Z} \cap b \mathbb{Z}$, en particular está en este conjunto. Como $[a,b]\in a\mathbb{Z}$, entonces $a|[a,b]$ y como $[a,b]\in b\mathbb{Z}$, entonces $b|[a,b]$.

Para la segunda parte, si $a\mid m$ y $b\mid m$, entonces $m\in a\mathbb{Z}$ y $m\in b\mathbb{Z}$, pero entonces $m\in a\mathbb{Z} \cap b\mathbb{Z} = [a,b]\mathbb{Z}$. De este modo, $[a,b]|m$.

$\square$

Así, el primer punto dice que $[a,b]$ es en efecto un múltiplo en común. El segundo punto es el que dice que «es el mínimo», pues a partir de la divisibilidad ahí escrita se deduce que $|[a,b]|\leq |m|$. Si pedimos que $m$ sea positivo, tenemos entonces que, en efecto, $[a,b]\leq m$. En resumen.

Corolario. Sean $a$ y $b$ enteros y $m$ un entero positivo múltiplo tanto de $a$ como de $b$. Entonces $m\geq [a,b]$.

Otra propiedad del mínimo común múltiplo

Tanto el mínimo común múltiplo, como el máximo común divisor, tienen muchas propiedades que se pueden demostrar. Hay dos caminos que usualmente funcionan: o bien usar la definición a partir de ideales, o bien usar las propiedades fundamentales de cada uno de los conceptos. Veamos algunos ejemplos para el mínimo común múltiplo.

La siguiente propiedad dice que ahora mostraremos que el mínimo común múltiplo «saca constantes» en cierto sentido. Veremos una demostración usando ideales.

Proposición. Sea $k$ un entero positivo, y $b,c$ enteros cualesquiera. Se cumple que $ [kb, kc] = k[b,c]. $

Demostración. Por definición, $[kb,kc]$ es el entero no negativo que genera al ideal $(kb)\mathbb{Z} \cap (kc)\mathbb{Z}$. Nos gustaría ver que dicho entero es $k[b,c]$, en otras palabras, hay que verificar la siguiente igualdad de conjuntos:

$$(kb)\mathbb{Z} \cap (kc)\mathbb{Z} = k[b,c]\mathbb{Z}.$$

Veamos que el lado izquierdo está contenido en el derecho. Tomemos un entero $m$ del lado izquierdo. Como es múltiplo de $kb$, lo podemos escribir como $m=kbr$ para $r \in \mathbb{Z}$. Como es múltiplo de $kc$, lo podemos escribir como $m=kcs$ para $s\in \mathbb{Z}$. Tenemos entonces $kbr=m=kcs$, de donde $br=cs$ (usando $k>0$). Así, $n=br=cs$ es simultánteamente múltiplo de $b$ y $c$, así que debe ser múltiplo de $[b,c]$, digamos $n=t[b,c]$. De este modo, tenemos que $m=kbr=kn=kt[b,c]$. Esto muestra que $m$ está en $k[b,c]\mathbb{Z}$.

Ahora veamos que el lado derecho está contenido en el izquierdo. Un entero $m$ en $k[b,c]\mathbb{Z}$ es de la forma $m=k[b,c]t$ para $t$ un entero. Como $[b,c]$ es múltiplo de $b$ y $c$, podemos escribir $[b,c]=rb$ y $[b,c]=sc$ para algunos enteros $r$ y $s$. Tenemos entonces que

$$m=k[b,c]t=krbt=(kb)(rt),$$

lo cual muestra que $m$ está en $(kb)\mathbb{Z}$ y que

$$m=k[b,c]t=ksct=(kc)(st),$$

lo cual muestra que $m$ está en $(kc)\mathbb{Z}$. Esto muestra que $m$ está en la intersección buscada.

$\square$

Mínimo común múltiplo y primos relativos

Cuando dos números positivos son primos relativos, es sencillo encontrar su mínimo común múltiplo: simplemente se multiplican. De hecho, esto es una caracterización para los números primos relativos.

Proposición. Sean $a$ y $b$ dos números enteros positivos. Se tiene que $(a,b)=1$ si y sólo si $[a,b]=ab$.

Demostración. Supongamos primero que $(a,b)=1$. Tenemos que $a|[a,b]$ y que $b|[a,b]$ Por una propiedad de primos relativos de la entrada anterior, podemos deducir que $ab|[a,b]$. A la vez, sabemos que $[a,b]$ divide a cualquier múltiplo en común de $a$ y $b$, en particular, a $ab$, así, $[a,b]|ab$. Por cómo interactúa la divisibilidad con los valores absolutos, obtenemos entonces que $[a,b]=|[a,b]|=ab$, como queríamos.

Ahora supongamos que $[a,b]=ab$. Tomemos un número $d$ que divida tanto a $a$ como a $b$. Veremos que ese número debe ser $1$ ó $-1$. Escribamos $a=dr$ y $b=ds$. Tomemos el número $n=drs$. Notemos que $n=as=br$, así que $n$ es un múltiplo común de $a$ y $b$. Por ello, debe ser múltiplo del mínimo común múltiplo de ambos, que estamos suponiendo que es $ab$. Así, existe un entero $k$ con $drs=kab$ y por lo tanto $$drs=kab=kdrds.$$ De aquí deducimos que $1=kd$, por lo que $d$ debe de dividir a $1$ y por lo tanto es $1$ ó $-1$, como queríamos.

$\square$

En realidad esta proposición tiene una versión más general. Siempre se cumple, para cualesquiera dos enteros $a$ y $b$, que $|ab|=[a,b]\cdot (a,b)$. Este es un problema clásico que estudiaremos más adelante.

Más adelante…

El mínimo común múltiplo y el máximo común divisor son dos conceptos que se utilizan mucho en la teoría de números enteros. En estas últimas dos entradas hemos platicado un poco acerca de ellos. Más adelante veremos que estas mismas nociones se pueden generalizar para otras estructuras algebraicas, como la de los polinomios.

Por ahora continuaremos estudiando teoría de la divisibiliad dentro de los números enteros. Es el momento de introducir otro de los conceptos estelares: el de números primos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra el mínimo común múltiplo de los números $24$ y $36$. Luego, encuentra su máximo común divisor.
  2. Demuestra que, para $a,b\in \mathbb{Z}$ se cumple: $[a,b] = [-a,b] = [a,-b] = [-a, -b].$
  3. Sean $a$ y $b$ enteros positivos. Muestra que $[a^2,b^2]=[a,b]^2$ y que, en general, para un entero $k\geq 1$ se cumple que $[a^n,b^n]=[a,b]^n$.
  4. ¿Cómo definirías el mínimo común múltiplo de tres números? ¿Y el máximo común divisor de tres números?
  5. Sean $a$, $b$, $c$ enteros. ¿Cómo están relacionados entre sí $[a,c]$, $[b,c]$ y $[a+b,c]$? ¿Será alguno de ellos la suma de los otros dos? Demuéstralo o da un contraejemplo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Máximo común divisor

Por Ana Ofelia Negrete Fernández

Deja un comentario

Introducción

La entrada anterior fue un poco técnica y habló acerca de ideales en los números enteros. Podemos apoyarnos de los ideales para construir otras nociones conocidas de la teoría de números enteros. En esta entrada hablaremos de una de ellas: la de máximo común divisor.

Quizás recuerdes la idea general del máximo común divisor a partir de lo que aprendiste en la educación básica. Por ejemplo, si tenemos a los números $14$ y $35$,y queremos encontrar su máximo común divisor, lo que se hacía es escribir los divisores de ambos:

  • Divisores de $14$: $1,2,7,14$.
  • Divisores de $35$: $1,5,7,35$.

Ya teniendo ambas listas, se elige número más grande que estén en ambas: el $7$.

Con lo que platicaremos en esta entrada vamos a recuperar esta misma noción, sin embargo lo haremos desde un punto de vista un poco más teórico, el cual nos permitirá entender más aspectos de divisibilidad de los máximos comunes divisores.

Definición de máximo común divisor

Recordemos, que en la entrada pasada vimos cómo encontrar al «ideal más pequeño» que tuviera a dos números $a$ y $b$ enteros dados.

Proposición. Si $a$ y $b$ son enteros, entonces:

  • El conjunto $M=\{ra+sb:r,s\in \mathbb{Z}\}$ es un ideal de $\mathbb{Z}$ que tiene a $a$ y a $b$.
  • Si $I$ es un ideal de $\mathbb{Z}$ que tiene a $a$ y a $b$, entonces $M\subseteq I$.

Como $M$ es el ideal más pequeño que tiene a $a$ y a $b$, le llamamos el ideal generado por $a$ y $b$, y lo escribimos como $\langle a,b\rangle$.

Además, en la entrada anterior también vimos que cualquier ideal de $\mathbb{Z}$ forzosamente es de la forma $k\mathbb{Z}$ para algún entero no negativo $k$, es decir, que consiste justo de los múltiplos de algún entero no negativo $k$. Esto nos permite plantear la siguiente definición.

Definición. Si $a$ y $b$ son enteros, definimos a su máximo común divisor como el entero no negativo $k$ tal que $$k\mathbb{Z}=\langle a,b\rangle.$$ A este número $k$ a veces se le denota por $\text{MCD}(a,b)$, o bien simplemente $(a,b)$.

Esta es una definición muy distinta de la que nos dan en la educación básica, sin embargo, pronto recuperaremos las propiedades familiares: veremos que en efecto es un divisor de $a$, es un divisor de $b$, y que de entre los divisores en común, es el más grande de ellos. Antes de pasar a las propiedades, veamos un ejemplo.

Ejemplo. Tomemos a los enteros $6$ y $14$. ¿Qué ideal $I$ generan? Es decir, ¿quién es $\langle 6,8\rangle$? Bueno, dicho ideal $I$ debe tener a $6$ y $14$, así que por cerradura de la resta tiene también a $14-6-8$, y similarmente debe tener a $8-6=2$. Pero recordemos que los ideales también son cerrados bajo producto por cualquier entero, así que al estar $2$ en $I$, debe pasar que todos los números pares están en $I$. Y en efecto, los números pares son un ideal de $\mathbb{Z}$ que tienen a $6$ y $14$. Con esto acabamos de demostrar que $\langle 6,14 \rangle = 2\mathbb{Z}$. De este modo, por definición, el máximo común divisor de $6$ y $14$ es igual a $2$.

$\triangle$

Propiedades del máximo común divisor

En esta sección veremos dos propiedades muy importantes del máximo común divisor. Por un lado, veremos que siempre se puede escribir «como combinación» de los números originales, en un sentido muy específico. Por otro lado, recuperaremos las «propiedades usuales» que queremos que se cumplan por lo que aprendimos en educación básica.

Proposición. Sean $a$ y $b$ números enteros. Entonces, existen enteros $r$ y $s$ tales que $$(a,b)=ra+sb.$$

Demostración. Por definición, $(a,b)$ es el entero tal que $\langle a,b \rangle =(a,b)\mathbb{Z}$, en particular, $(a,b)$ está en $\langle a,b\rangle$. Pero también ya sabemos que $$\langle a,b \rangle = \{ra+sb:r,s\in \mathbb{Z}\}.$$ Como $(a,b)$ está en $\langle a,b \rangle$, entonces se puede escribir de la forma de los elementos del conjunto de la derecha también, es decir, existen enteros $r$ y $s$ tales que $$(a,b)=ra+sb.$$

$\square$

Como estamos poniendo a $(a,b)$ de la forma $ra+sb$, en donde los coeficientes de $a$ y $b$ son los números enteros $r$ y $s$, decimos que $(a,b)$ se puede escribir como una combinación lineal entera de $a$ y $b$. La proposición anterior nos demuestra la existencia de dicha combinación lineal, sin embargo no nos dice exactamente cómo encontrarla. Más adelante veremos el algoritmo de Euclides, el cual nos da una forma práctica de encontrar al máximo común divisor de dos números como combinación lineal de ellos.

Veamos ahora el resultado que nos dice que, en efecto, el máximo común divisor divide a cada número, y que es «el más grande» que hace esto.

Proposición. Sean $a$ y $b$ números enteros. Entonces, se cumple lo siguiente:

  • $(a,b)|a$ y $(a,b)|b$.
  • Si $d$ es algún otro número tal que $d|a$ y $d|b$, entonces $d|(a,b)$.

Demostración. Notemos que $a\in \langle a, b\rangle$, y que por definición $\langle a,b \rangle = (a,b) \mathbb{Z}$. De este modo, $a$ es múltiplo de $(a,b)$. Análogamente, $b$ es múltiplo de $(a,b)$. Esto muestra el primer inciso.

Ahora supongamos que $d$ es otro número tal que $d|a$ y $d|b$. Por la proposición anterior, existen enteros $r$ y $s$ tales que $(a,b)=ra+sb$. Como $d|a$, entonces $d|ra$. Como $d|b$, entonces $d|sb$. Así, $d|ra+sb=(a,b)$, como queríamos.

$\square$

La proposición anterior sí dice que el máximo común divisor divide a ambos, sin embargo no es totalmente directo por qué es el «máximo» en tamaño. La segunda parte habla más bien de una divisibilidad. Pero esto se traduce rápidamente a una desigualdad con la ayuda de las propiedades de la divisibilidad. Observa que si $d$ es un número tal que $d|a$ y $d|b$, entonces $d|(a,b)$. Tenemos entonces que $|d|\leq |(a,b)|$. Pero $(a,b)$ siempre es no negativo por definición, así que $|d|\leq (a,b)$. En resumen, tenemos el siguiente resultado.

Corolario. Si $a$ y $b$ son enteros y $d$ es un entero tal que $d|a$ y $d|b$, entonces $|d|\leq (a,b)$.

Números primos relativos (de máximo común divisor igual a uno)

Una situación muy especial en la teoría de los números ocurre cuando el máximo común divisor de dos números es igual a $1$.

Definición. Decimos que dos números enteros $a$ y $b$ son primos relativos si su máximo común divisor es igual a $1$. En símbolos, son primos relativos si $(m,n)=1$.

Por lo que hemos discutido hasta ahora, algunas de las consecuencias de que dos números $a$ y $b$ sean primos relativos son las siguientes:

  • Si $d$ es un número que divide a $a$ y a $b$, entonces $|d|\leq (a,b)=1$, es decir, $d=1$ o $d=-1$. De este modo, los únicos divisores que tienen en común son el $1$ y el $-1$.
  • El ideal generado por $a$ y $b$ es $1\cdot \mathbb{Z} = \mathbb{Z}$, es decir, consiste de todos los enteros.
  • Por esa misma razón, se tiene que $\{ra+sb: r,s \in \mathbb{Z}\}=\mathbb{Z}$, en otras palabras, cualquier entero es combinación lineal entera de $a$ y de $b$.
  • En particular, el $1$ es combinación lineal entera de $a$ y de $b$, es decir, existen enteros $r,s$ tales que $ra+sb=1$.

Estas consecuencias son prácticamente inmediatas de la definición, y es recomendable que intentes deducirlas por tu cuenta.

Veamos algunas otras propiedades que relacionan a los números primos relativos, con divisibilidad de algunas expresiones.

Proposición. Sean $a,b,c$ números enteros . Si $a\mid bc$ y $(a,b) = 1$, entonces $a\mid c.$

Demostración. Como $a$ divide a $bc$, existe $x \in \mathbb{Z}$ tal que $ax = bc$. Como $a$ y $b$ son primos relativos, sabemos que existen enteros $r$ y $s$ tales que $1 = ra+sb$. Multipliquemos esta última igualdad por $c$. Tenemos entonces que:
$$ c = rac + sbc = rac+ sax = a (rc+sx).$$

De aquí obtenemos la divisibilidad $a\mid c$ que buscábamos.

$\square$

En la proposición anterior es crucial la hipótesis de que $a$ y $b$ sean primos relativos. Por ejemplo, $7|28=14\cdot 2$, pero no pasa que $7|2$. Es decir, usualmente si dividimos a un producto, no se cumple que dividamos a cualquiera de sus factores.

A continuación tenemos otro resultado con un estilo similar.

Proposición. Sean $a,b,c \in \mathbb{Z}.$ Si $a\mid c$, $b\mid c$ y $(a,b) =1,$ entonces $ab \mid c$.

Demostración. Ya que $a,b$ son primos relativos, existen $m,n \in \mathbb{Z}$ tales que $1=am + bn $. Multipliquemos dicha ecuación por $c$: $$c=cam + cbn.$$

Como $a\mid c$ y $b\mid c$, existen $q,r \in \mathbb{Z}$ tales que $aq = c$ y $br = c$. Sustituyendo esto en la ecuación anterior, obtenemos que: $$c=cam + cbn = bram + aqbn = ab(rm+qn).$$

Esta igualdad justo nos dice que $ab\mid c$, como queríamos.

$\square$

Intenta encontrar un contraejemplo cuando no se cumple la hipótesis de que $a$ y $b$ son números primos relativos.

Más adelante…

Dejaremos el estudio del máximo común divisor hasta aquí por el momento. En la siguiente entrada hablaremos de un concepto muy cercano: el de mínimo común múltiplo. Así como en el caso de esta entrada, introduciremos la noción a partir de un contexto de ideales, para luego ver ejemplos y algunas propiedades clave.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra todas las consecuencias de ser primos relativos de la lista enunciada en la entrada.
  2. Prueba que dos enteros consecutivos siempre son primos relativos. Usa esto para demostrar que siempre que se eligen $51$ números distintos entre $1$ y $100$, forzosamente debes tener dos de ellos que sean primos relativos.
  3. Sea $m$ un entero positivo. Demuestra que $(a,b)=1$ si y sólo si $(a^m, b^m) =1.$
  4. De acuerdo a la entrada, al tomar dos números $a$ y $b$ podemos encontrar enteros $r$ y $s$ tales que $(a,b)=ra+sb$. Demuestra que siempre sucede que $(r,s)=1$.
  5. Encuentra el máximo común divisor de $91$ y $70$ e intenta escribirlo como combinación lineal entera de ellos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

1.6. SUBESPACIO GENERADO POR UN CONJUNTO: definición y ejemplos

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

Introducción

Queremos saber:
¿Podemos describir el conjunto de todas las combinaciones lineales de un conjunto dado?
Dado un elemento de un conjunto $A$, ¿cómo saber si podemos obtenerlo como combinación lineal de otro conjunto $B$?
¿Qué características cumple el conjunto de todas las combinaciones lineales de un conjunto cualquiera?

SUBESPACIO GENERADO

Definición: Sean $V$ un $K$ – espacio vectorial y $S$ un subconjunto de $V$. Diremos que el subespacio de $V$ generado por $S$ es:
el conjunto de combinaciones lineales de $S$, si $S\not=\emptyset$,
o bien, $\{\theta_V\}$, si $S=\emptyset$.
Se denota por $\langle S\rangle$.

Si $W$ es un subespacio de $V$, se dice que $S$ genera a $W$, o que $S$ es un conjunto generador de $W$, si $\langle S\rangle =W$.

Observación: La proposición de la entrada anterior nos menciona tres importantes propiedades del conjunto de todas las combinaciones de un subconjunto dado, en particular, que forma un subespacio.

Nota: Es común que en algunos libros se denote como $span(S)$ en lugar de $\langle S\rangle$. Además, se suele escribir $\langle v_1,…,v_n\rangle$ cuando $S=\{v_1,…,v_n\}$.

Ejemplos:

  • Sean $K=\mathbb{R}$, $V=\mathbb{R}^3$ y $S=\{(1,0,0),(0,1,0),(0,0,1)\}=\{e_1,e_2,e_3\}$.
    $\langle S\rangle =V$.

Justificación: Para cualesquiera $a,b,c\in\mathbb{R}$, tenemos que $a(1,0,0)+b(0,1,0)+c(0,0,1)=(a,b,c)\in V$, así que $\langle S\rangle\subseteq V$.
Para cualquier $(x,y,z)\in V$, tenemos que $(x,y,z)=x\,e_1+y\,e_2+z\,e_3\in S$, por lo que $V\subseteq\langle S\rangle$.

  • Sean $K=\mathbb{R}$, $V=\mathcal{P}_2(\mathbb{R})$ y $S=\{1,1-x,1-x-x^2\}$.
    $\langle S\rangle =V$.

Justificación: Para cualesquiera $\lambda_1,\lambda_2,\lambda_3\in\mathbb{R}$, tenemos que $\lambda_1(1)+\lambda_2(1-x)+\lambda_3(1-x-x^2)$
$=(\lambda_1+\lambda_2+\lambda_3)+(-\lambda_2-\lambda_3)x+(-\lambda_3)x^2\in V$, así que $\langle S\rangle\subseteq V$.
Para cualquier $a+bx+cx^2\in V$, tenemos que $a+bx+cx^2=(a+b)(1)+(c-b)(1-x)+(-c)(1-x-x^2)\in S$, por lo que $V\subseteq\langle S\rangle$.

  • Sean $K=\mathbb{R}$, $V=\mathbb{R}^3$ y $S=\{(1,0,0),(1,-1,0),(1,1,-1)\}$.
    $\langle S\rangle =V$.

Justificación: Para cualesquiera $a,b,c\in\mathbb{R}$, tenemos que $a(1,0,0)+b(1,-1,0)+c(1,1,-1)=(a+b+c,-b+c,-c)\in V$, así que $\langle S\rangle\subseteq V$.
Para cualquier $(x,y,z)\in V$, tenemos que $(x,y,z)=(x+y+2z)(1,0,0)+(-y-z)(1,-1,0)+(-z)(1,1,-1)\in S$, por lo que $V\subseteq\langle S\rangle.$

  • Sean $K=\mathbb{R}$, $V=\mathcal{M}_{2\times 2}(\mathbb{R})$ y $S=\left\{ \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} , \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \right\}$.
    $\langle S\rangle =\left\{ \begin{pmatrix} a & a \\ b & a \end{pmatrix} \bigg\vert a,b\in\mathbb{R}\right\}$.

Justificación: \begin{align*}
\langle S\rangle &= \bigg\{ \lambda \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix} + \mu \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \bigg\vert \,\lambda,\mu\in\mathbb{R}\bigg\}\\
&= \bigg\{ \begin{pmatrix} \lambda & \lambda \\ \lambda & \lambda \end{pmatrix} + \begin{pmatrix} \mu & \mu \\ 0 & \mu \end{pmatrix} \bigg\vert \lambda ,\mu\in\mathbb{R} \bigg\} \\
&= \bigg\{ \begin{pmatrix} \lambda +\mu & \lambda + \mu \\ \lambda & \lambda +\mu \end{pmatrix} \bigg\vert\, \lambda ,\mu\in\mathbb{R} \bigg\} \\
&= \bigg\{ (\lambda +\mu)\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} + \lambda \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \bigg\vert\, \lambda ,\mu\in\mathbb{R} \bigg\} \\
&= \bigg\{ a\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} + b\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} \bigg\vert\, a,b\in\mathbb{R} \bigg\} \\
&= \bigg\{ \begin{pmatrix} a & a \\ b & a \end{pmatrix} \bigg\vert \,a,b\in\mathbb{R}\bigg\}
\end{align*}

Nota: Puede ocurrir que $W\subseteq\langle S\rangle$ y $W\not=\langle S\rangle$. En ese caso, $S$ no genera a $W$.
Por ejemplo, si $W=\{(a,a)|a\in\mathbb{R}\}$ y $S=\{e_1,e_2\}$, es claro que $\langle S\rangle =\mathbb{R}^2$, por lo cual, $W\subseteq\langle S\rangle$, pero no son iguales.

Observación: Si $S\subseteq W$, entonces $\langle S\rangle\subseteq W$.
Si además todo vector en $W$ es combinación lineal de vectores de $S$, entonces $W\subseteq\langle S\rangle$ y en ese caso tendremos que $\langle S\rangle= W.$

Como el subespacio generado por un conjunto es un conjunto, nos interesa analizar algunas operaciones y ver qué relaciones encontramos.

Sea $V=\mathbb{R}^2$ con $K=\mathbb{R}$.
Sean $S_1=\{(1,0)\}$, $S_2=\{(0,1)\}$ y $S_3={(1,1)}$.

  • $S_1\cup S_2=\{(1,0),(0,1)\}$
  • $S_1\cap S_2=\emptyset$
  • $S_1\cup S_3=\{(1,0),(1,1)\}$
  • $S_1\cap S_3=\emptyset$
  • $\langle S_1\rangle =\{(x,0)|x\in\mathbb{R}\}$
  • $\langle S_2\rangle =\{(0,y)|y\in\mathbb{R}\}$
  • $\langle S_3\rangle =\{(x,x)|x\in\mathbb{R}\}$
  • $\langle S_1\cup S_2\rangle$$=\langle\{(1,0),(0,1)\}\rangle$
    Sean $a\in\mathbb{R}$, $b\in\mathbb{R}$
    Como $a(1,0)+b(0,1)=(a,0)+(0,b)=(a,b)$ y $a$ y $b$ son números reales cualesquiera, entonces para cualquier $(x,y)\in\mathbb{R}$ podremos encontrar una combinación lineal de $S_1\cup S_2$ cuyo resultado sea $(x,y)$
    Por lo tanto, $\langle S_1\cup S_2\rangle=\mathbb{R}^2$.
  • $\langle S_1\rangle\cup\langle S_2\rangle$$=\{(x,0)|x\in\mathbb{R}\}\cup\{(0,y)|y\in\mathbb{R}\}$
    Es decir, únicamente podemos obtener valores en los ejes de nuestro plano cartesiano.
  • $\langle S_1\cap S_3\rangle$$=\emptyset$$=(0,0)$
  • $\langle S_1\rangle\cap\langle S_3\rangle$$=\langle\{(x,0)|x\in\mathbb{R}\}\rangle\cap\langle\{(x,x)|x\in\mathbb{R}\}\rangle$
    Una combinación lineal pertenece a este conjunto si el resultado puede expresarse con únicamente elementos de $S_1$ y con únicamente elementos de $S_2$.
    ¿Qué elementos de $\mathbb{R}^2$ tienen en la segunda entrada al cero y en ambas entradas al mismo número? Solo en $(0,0)$
    Por lo tanto, $\langle S_1\rangle\cap\langle S_3\rangle =(0,0)$.

Tarea Moral

  1. Encuentra un $K_1$ campo y un $K_1$ – espacio vectorial donde puedas definir un subconjunto infinito $S_1$ tal que $\langle S_1\rangle$ sea finito.
  2. Encuentra un $K_2$ campo y un $K_2$ – espacio vectorial donde puedas definir un subconjunto $S_2$ de un solo elemento tal que $\langle S_2\rangle$ sea infinito.
  3. Toma en cuenta los subconjuntos definidos al final de esta entrada donde $K=\mathbb{R}$ y $V=\mathbb{R}^2$. Describe la relación que existe entre:
    • $\langle S_1\cup S_3\rangle$ y $\langle S_1\rangle\cup\langle S_3\rangle$
    • $\langle S_1\cap S_2\rangle$ y $\langle S_1\rangle\cap\langle S_2\rangle$

Más adelante…

Muchas veces en matemáticas buscamos el mayor / menor conjunto con el cual obtengamos ciertas propiedes. Siguiendo esta idea, veremos un nuevo concepto: conjunto linealmente independiente.

Entradas relacionadas