[latexpage]

En esta entrada les contaré una solución sencilla a una de las partes del Problema 6 de la Olimpiada Internacional de Matemáticas de este año. El problema dice lo siguiente:

Se tienen $n\geq 2$ segmentos en el plano tales que cada par de segmentos se intersectan en un punto interior a ambos, y no hay tres segmentos que tengan un punto en común. Mafalda debe elegir uno de los extremos de cada segmento y colocar una rana mirando hacia el otro extremo. Luego silbará $n-1$ veces. En cada silbido, cada rana saltará inmediatamente hacia adelante hasta el siguiente punto de intersección sobre su segmento. Las ranas nunca cambian las direcciones de sus saltos. Mafalda quiere colocar las ranas de tal forma que nunca dos de ellas ocupen al mismo tiempo el mismo punto de intersección.

A) Demuestra que si $n$ es impar, Mafalda siempre puede lograr su objetivo.
B) Demuestra que si $n$ es par, Mafalda nunca logrará su objetivo

Es un lindo problema de geometría combinatoria y se puede jugar con él. El objetivo de esta entrada es dar una solución muy sencilla a la Parte A que fue propuesta durante las reuniones de jurado.  Para disfrutar un poco esta solución es recomendable intentarlo un rato antes de pasar a la siguiente sección. La solución de la Parte B y otras soluciones se pueden ver en www.imo-official.org (hay que buscarlas en el menú de Problemas).

Un ejercicio de inducción

Haremos un paso intermedio. Es un problema sencillo que usualmente se ve en la primer clase de inducción. Dice lo siguiente:

Se dibuja una cantidad finita de rectas en el plano de modo que no hay $3$ concurrentes. Muestra que se pueden pintar las regiones definidas por las rectas con verde y negro de modo que no haya dos regiones juntas del mismo color.

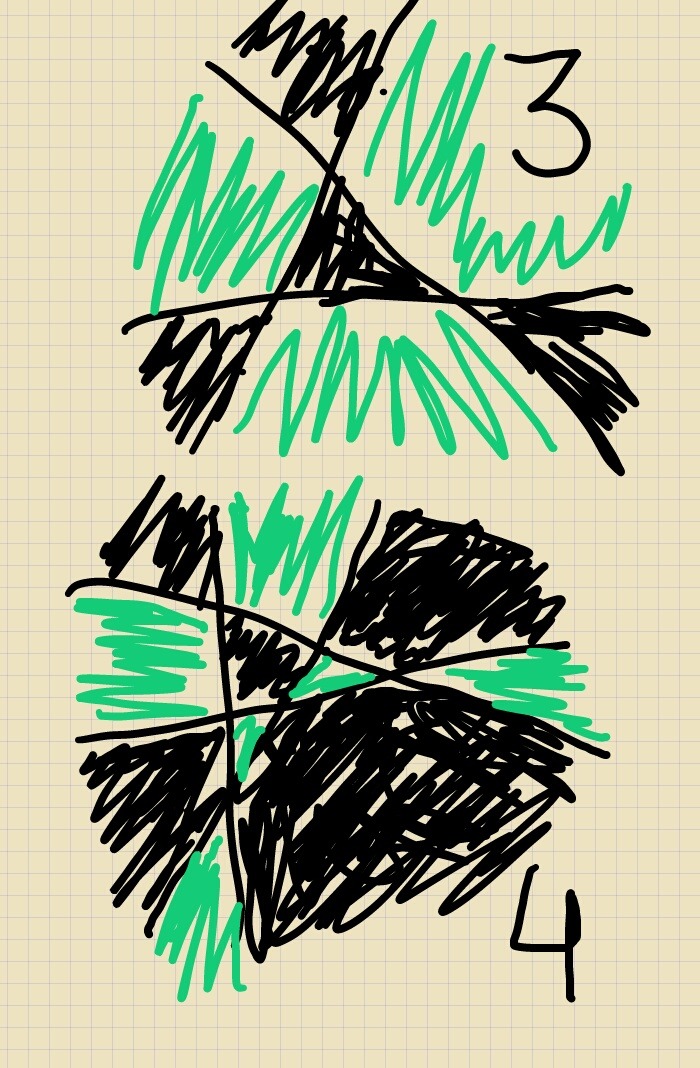La prueba va así. Si sólo hay una recta, ponemos un lado de verde y el otro de negro. Si sabemos cómo lograrlo para $n$ rectas y ahora tenemos $n+1$, basta quitar una recta, colorear, y al agregar la recta $n+1$, intercambiar los colores de todas las regiones que quedan en uno de los semiplanos que define. En la imagen hay dos ejemplos, uno para $n=3$ y uno para $n=4$.

Las ranas y los colores

Hagamos la Parte A. Supongamos que $n$ es impar y que tenemos los segmentos como en el problema (se intersectan de dos en dos, pero no hay tres por el mismo punto). Extendamos los segmentos a rectas por todo el plano. Por la sección anterior, podemos colorear las regiones con verde y negro sin regiones del mismo color adyacentes.

Ahora, fijémonos en una recta específica. Si «llegamos caminando» por uno de sus extremos, a nuestra mano derecha tendremos un color, digamos negro. Como $n$ es impar, si llegamos caminando por el otro extremo, a nuestra mano derecha tendremos el otro color (verde). Ayuda volver a ver los ejemplos de los casos $3$ y $4$.

Como a las ranas les gusta más el color verde, las colocaremos para que al «ir entrando a la recta», a su lado derecho todas tengan el color verde.

Veamos que este acomodo funciona. Lo primero es notar que cada vez que Mafada silba, las ranas avanzan usando el siguiente segmento, cuya región derecha tiene color distinto a la del anterior. La observación clave es que entonces, en cada brinco, todas las ranas tienen a la derecha una región del mismo color. Esta región va alternando verde, negro, verde, etc, pero el color es el mismo para todas las ranas.

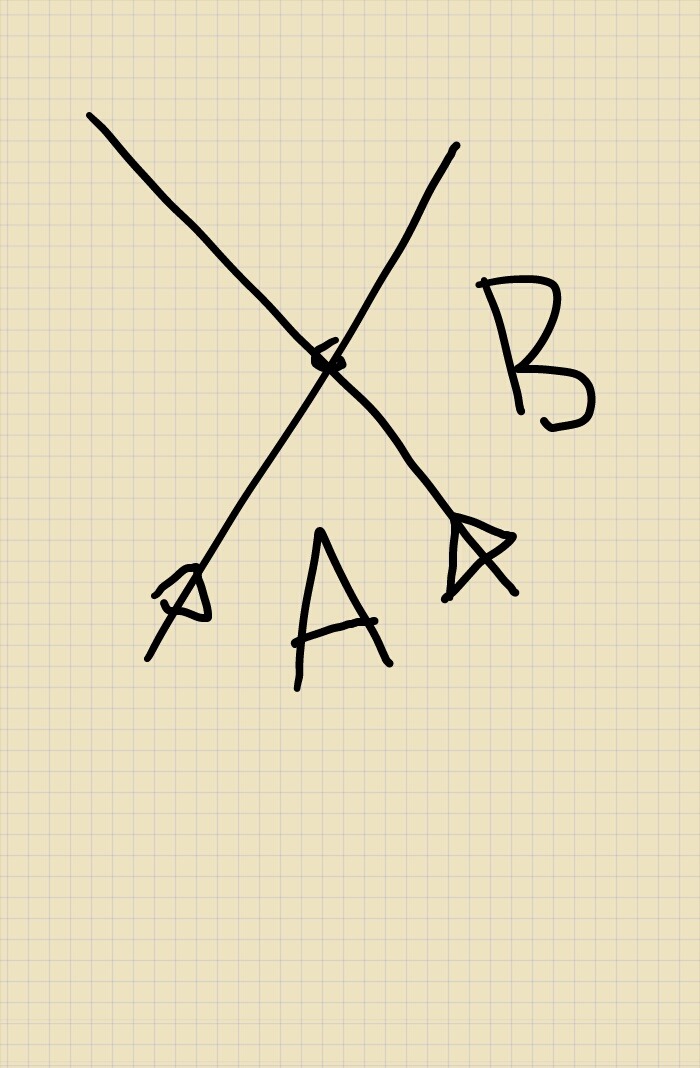Con esto es fácil ver que las ranas nunca llegan al mismo punto. Veamos la figura.

Si las ranas llegan al punto de intersección al mismo tiempo, entonces las regiones $A$ y $B$ serían del mismo color por la observación anterior. Pero esto sería una contradicción a  la manera en la que coloreamos el plano, la cual garantiza que $A$ y $B$ tienen distinto color pues son adyacentes. Entonces las ranas nunca coinciden, y esto termina la prueba.