$\textcolor{Red}{\textbf{Teorema de la Función Inversa $f:\mathbb{R}\rightarrow\mathbb{R}$}}$

$\textbf{Teorema 1.}$ Sea $f:A\subset\mathbb{R}\rightarrow\mathbb{R}$ definida sobre el abierto $A\subset\mathbb{R}$ y sea $x_{0}\in A$.
(1) Supóngase que f tiene derivada continua y que $f'(x_{0})\neq 0$.
(2) Entonces existe un intervalo abierto $I$ que contiene al punto $x_{0}$ y un intervalo abierto $j$ que contiene a $f(x_{0})$, tal que la función $f:I\rightarrow J$ es uno a uno y sobre.
(3) Además, la función inversa $f^{-1}:J\rightarrow I$ también tiene derivada continua y para un punto $y\in J$, si $x\in I$ es tal que $f(x)=y$, entonces
$$\left(f^{-1}\right)'(y)=\frac{1}{f'(x)}$$

$\textbf{Ejercicio.}$ Obtener la tesis del teorema de la función inversa como aplicación del teorema de la función implícita

$\small{Solución}$

Sea $y=f(x)$ una función real de variable real con derivada continua sobre un conjunto abierto A y sea $x_{0}$ un punto de A donde $f'(x_{0})\neq0$.

Considere la función $F(x,y)=y-f(x)$ y calculemos sus derivadas parciales. Así
$$\frac{\partial F}{\partial x}=-f'(x)~~y\frac{\partial F}{\partial y}=1$$ Nótese que $F,\displaystyle{\frac{\partial F}{\partial x},~~\frac{\partial F}{\partial y}}$ son continuas sobre el conjunto
$$B=\left\{(x,y)\in\mathbb{R}^{2}~|~x\in A \right\}$$

Considere ahora como solución inicial el punto $(x_{0},y_{0})$ donde $y_{0}=f(x_{0})$. Tenemos que
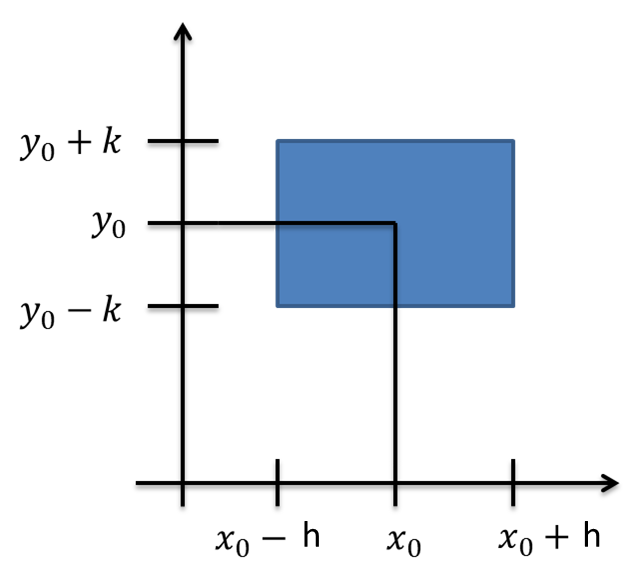
$$F(x_{0},y_{0})=0~~y\frac{\partial F}{\partial x}(x_{0},y_{0})\neq0$$ De manera que se cumplen las hipótesis del Teorema de la Función Implicita. Luego entonces cerca del punto $(x_{0},y_{0})$ la variable x puede representarse en términos de la variable y. Estos expresado formalmente nos dice que existe una única función implicita $x=g(y)$ con dominio un intervalo $J=(y_{0}-k,y_{0}+k)$ y con rango $I=(x_{0}-h,x_{0}+h)$ tal que $$g(y_{0})=x_{0}$$ y, para toda y, en el intervalo J $$F(g(y),y)=0~y~~~\frac{\partial F}{\partial x}(g(y),y)\neq 0$$
ademas, g y su derivada $g’$ son continuas sobre J, y
$$g'(y)=-\frac{\frac{\partial F}{\partial y}(g(y),y)}{\frac{\partial F}{\partial x}(g(y),y)}=-\frac{1}{-f'(g(y))}=\frac{1}{f'(x)}$$La función g que ha sido determinada no es otra que la función inversa

$\textbf{Ejemplo.}$ Sea f la función definida por la regla de correspondencia $f(x)=-x^{5}-x$. Si calculamos su derivada, tenemos $f'(x)=-5x^{4}-1$. Observese que $f'(x)<0$ para toda x en los reales, por lo que f es decreciente sobre toda la recta real y a su vez es uno a uno.\Concluimos así que la inversa de f está definida sobre toda la recta real y que su gráfica es decreciente. Sin embargo, no se puede obtener la regla de correspondencia para la inversa. Sin embargo, podemos calcular su derivada. Sea y cualquier número real y supóngase que x es tal que $f^{-1}(y)=x$. Así
$$\left(f^{-1}\right)'(y)=\frac{1}{f'(f^{-1}(y))}=\frac{1}{f'(x)}=-\frac{1}{5x^{4}+1}$$

$\textcolor{Red}{\textbf{Teorema de la Función Inversa (sistema $f_{i}:\mathbb{R}^{n}\rightarrow\mathbb{R}$)}}$

Sea $U\subset\mathbb{R}^{n}$ un abierto y sean
$$\begin{matrix}
f_{1}:U\rightarrow\mathbb{R} \\
\vdots \\
f_{n}:U\rightarrow\mathbb{R}
\end{matrix}$$
con derivadas parciales continuas. Considerar las ecuaciones

$f_1(x_1,x_2,…,x_n)= y_1$
$f_2(x_1,x_2,…,x_n)= y_2$
$\vdots\\$
$f_n(x_1,x_2,…,x_n)= y_n$
Tratamos de resolver las n-ecuaciones para $x_1,x_2,… x_n$como funciones de $y_1,y_2,… y_n$

La condición de existencia para la solución en una vecindad del punto $x_0$ es que el determinante de la matriz $Df(x_0)$ y $f=(f_i,f_2,… f_n)$ sean distintos de cero. Explícitamente:

$\displaystyle \frac{\partial(f_1,f_2,…,f_n)}{\partial(x_1,x_2,…,x_n)}|_{x=x_0}= J(f)(x_0)= \left| \begin{array}{ccc} \displaystyle\frac{\partial f_1}{\partial x_1} (x_0)&\ldots&\displaystyle\frac{\partial f_1}{\partial x_1}(x_0)\\ \vdots & & \vdots\\
\displaystyle\frac{\partial f_n}{\partial x_1}(x_0)&\ldots&\displaystyle\frac{\partial f_n}{\partial x_n}(x_0) \end{array}\right|\neq 0$

entonces el sistema anterior se puede resolver de manera ‘unica como $x=g(y)$ para $x$ cerca de $x_{0}$ y y cerca de $y_{0}$

$\textbf{Nota:}$ La cuestión de existencia se responde por medio del teorema general de la función implícita aplicado a las funciones $y_i-f_i(x_1,x_2,…,x_n)$ con las incognitas $x_1,x_2,…,x_n$.

$\small{Solución.}$ Aquí las funciones son
$$u(x,y)=f_{1}(x,y)=\frac{x^{4}+y^{4}}{x},~~y~~v(x,y)=f_{2}(x,y)= sen~x+\cos~y$$
De acuerdo al teorema de la función inversa
$$\frac{\partial(f_{1},f_{2})}{\partial(x,y)}=\left|\begin{matrix}
\frac{\partial f_{1}}{\partial x} & \frac{\partial f_{1}}{\partial y} \\
\frac{\partial f_{2}}{\partial x} & \frac{\partial f_{2}}{\partial y}
\end{matrix}\right|$$
$$=\left|\begin{matrix}
\frac{3x^{4}-y^{4}}{x^{2}} & \frac{4y^{3}}{x} \\
\cos~x & -sen~y
\end{matrix}\right|= \frac{sen~y}{x^{2}}(y^{4}-3x^{4})-\frac{4y^{3}}{x}\cos~x$$
por lo tanto, en los puntos donde la expresión anterior no se anula, se puede resolver para $x$,$y$ en términos de $u$ y $v$.

Mas aún, si consideramos las expresiones:
$G(x,y,u,v)=x-f(u,v)=0$
$H(x,y,u,v)=y-g(u,v)=0$

Lo que pretendemos es «despejar» de ella a $u$ y $v$ en términos de $x$ e $y$ y poder establecer así las funciones $u=\varphi(x,y), v=\psi(x,y)$. Entonces el T.F.Im. (tercera versión) nos da las condiciones para que podamos hacer esto. Sea $P (x,y,u,v)\epsilon\mathbb{R}^4$ un punto tal que $G(p)=H(p)=0$. Supongamos que en una bola de centro en P las derivadas parciales de $G$ y $H$ son continuas. Si el jacobiano.

$$\displaystyle\frac{\partial(G,H)}{\partial(u,v)}=\left|\begin{matrix}
\frac{\partial G}{\partial u} & \frac{\partial G}{\partial v} \\
\frac{\partial H}{\partial u} & \frac{\partial H}{\partial v}
\end{matrix}\right|=\left|\begin{matrix}
-\frac{\partial f}{\partial u} & -\frac{\partial f}{\partial v} \\
-\frac{\partial g}{\partial u} & -\frac{\partial g}{\partial v}
\end{matrix}\right|=\left|\begin{matrix}
\frac{\partial f}{\partial u} & \frac{\partial f}{\partial v} \\
\frac{\partial g}{\partial u} & \frac{\partial g}{\partial v}
\end{matrix}\right|\neq0$$

en $P$, entonces es posible «despejar» de ellas a $u$ y $v$ en terminos de $x$ e $y$, y establecer así funciones $u=\varphi(x,y), v=\varphi(x,y)$ definidas en una vecindad $V$ de $(x,y)=F(u,v)$, las cuales tienen derivadas parciales continuas en $V$ que se pueden calcular como

$\displaystyle\frac{\partial G}{\partial u}=-\displaystyle\frac{\partial f}{\partial u} ~,~ \displaystyle\frac{\partial G}{\partial v}=-\displaystyle\frac{\partial f}{\partial v} ~,~ \displaystyle\frac{\partial H}{\partial u}=-\displaystyle\frac{\partial g}{\partial u} ~,~ \displaystyle\frac{\partial H}{\partial v}=-\displaystyle\frac{\partial g}{\partial v}$

$$\displaystyle\frac{\partial u}{\partial x}=-\displaystyle\frac{\displaystyle\frac{\partial(G,H)}{\partial((x,v)}}{\displaystyle\frac{\partial(G,H)}{\partial(u,v)}}=-\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det
\left| \begin{array}{cc}
\displaystyle\frac{\partial G}{\partial x} & \displaystyle\frac{\partial G}{\partial v}\\
\displaystyle\frac{\partial H}{\partial x} & \displaystyle\frac{\partial H}{\partial v}
\end{array} \right|= -\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det \left|\begin{array}{cc}
1 & -\displaystyle\frac{\partial f}{\partial v}\\
0 & -\displaystyle\frac{\partial g}{\partial v}\end{array}\right|=\displaystyle\frac{\displaystyle\frac{\partial g}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}
$$

Por lo tanto: $\displaystyle\frac{\partial u}{\partial x} = \displaystyle\frac{\displaystyle\frac{\partial g}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}$

$$\displaystyle\frac{\partial u}{\partial y}=-\displaystyle\frac{\displaystyle\frac{\partial(G,H)}{\partial((y,v)}}{\displaystyle\frac{\partial(G,H)}{\partial(u,v)}}=-\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det
\left| \begin{array}{cc}
\displaystyle\frac{\partial G}{\partial y} & \displaystyle\frac{\partial G}{\partial v}\\
\displaystyle\frac{\partial H}{\partial y} & \displaystyle\frac{\partial H}{\partial v}
\end{array} \right|= -\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det \left|\begin{array}{cc}
0 & -\displaystyle\frac{\partial f}{\partial v}\\
1& -\displaystyle\frac{\partial g}{\partial v}\end{array}\right|=-\displaystyle\frac{\displaystyle\frac{\partial f}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}
$$

Por lo tanto: $\displaystyle\frac{\partial u}{\partial y} = -\displaystyle\frac{\displaystyle\frac{\partial f}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}$

$$\displaystyle\frac{\partial v}{\partial x}=-\displaystyle\frac{\displaystyle\frac{\partial(G,H)}{\partial((u,x)}}{\displaystyle\frac{\partial(G,H)}{\partial(u,v)}}=-\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det
\left| \begin{array}{cc}
\displaystyle\frac{\partial G}{\partial u} & \displaystyle\frac{\partial G}{\partial x}\\
\displaystyle\frac{\partial H}{\partial u} & \displaystyle\frac{\partial H}{\partial x}
\end{array} \right|= -\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det \left|\begin{array}{cc}
-\displaystyle\frac{\partial f}{\partial u} & 1\\
-\displaystyle\frac{\partial g}{\partial u} & 0 \end{array}\right|=-\displaystyle\frac{\displaystyle\frac{\partial g}{\partial u}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}$$

$$\displaystyle\frac{\partial v}{\partial y}=-\displaystyle\frac{\displaystyle\frac{\partial(G,H)}{\partial((u,y)}}{\displaystyle\frac{\partial(G,H)}{\partial(u,v)}}=-\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det
\left| \begin{array}{cc}
\displaystyle\frac{\partial G}{\partial u} & \displaystyle\frac{\partial G}{\partial y}\\
\displaystyle\frac{\partial H}{\partial u} & \displaystyle\frac{\partial H}{\partial y}
\end{array} \right|= -\displaystyle\frac{1}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}det \left|\begin{array}{cc}
-\displaystyle\frac{\partial f}{\partial u} & 0\\
-\displaystyle\frac{\partial g}{\partial u} & 1 \end{array}\right|=\displaystyle\frac{\displaystyle\frac{\partial f}{\partial u}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}$$

En resumen tenemos: Sean $f,g: U \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$ funciones definidas en el conjunto abierto $U$ de $\mathbb{R}^2$. Sean $x=f(u,v)$, $y=g(u,v)$.

Suponga que alguna bola $B$ de $\mathbb{R}^2$ con centro $(u,v)$, las derivadas parciales $\displaystyle\frac{\partial f}{\partial u}$, $\displaystyle\frac{\partial f}{\partial v}$, $\displaystyle\frac{\partial g}{\partial u}$, $\displaystyle\frac{\partial g}{\partial v}$ son continuas.

Si el jacobiano $\displaystyle\frac{\partial(f,g)}{\partial (u,v)}$ es no nulo en $(u,v)$ entonces $\exists$ una vecindad $V$ de $\bar{x},\bar{y}$ donde podemos definir «funciones inversas» $u=\varphi(x,y),v=\psi(x,y)$ es decir tales que $$u=\varphi(x,y), v=\psi(x,y)$, y $f(\varphi(x,y), \psi(x,y))=x ,g(\varphi(x,y), \psi(x,y))=y$$

para $(x,y) \epsilon V$ las cuales tienen derivadas parciales continuas en $V$ que se calculan como

$$\displaystyle\frac{\partial u}{\partial x} = \displaystyle\frac{\displaystyle\frac{\partial g}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}}\ ~,~ \displaystyle\frac{\partial u}{\partial y} = -\displaystyle\frac{\displaystyle\frac{\partial f}{\partial v}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}} ~,~ \displaystyle\frac{\partial v}{\partial x}=-\displaystyle\frac{\displaystyle\frac{\partial g}{\partial u}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}} ~,~ \displaystyle\frac{\partial v}{\partial y}=\displaystyle\frac{\displaystyle\frac{\partial f}{\partial u}}{\displaystyle\frac{\partial(f,g)}{\partial(u,v)}} \ast$$

Ahora bien con las funciones $u=\varphi(x,y),~~v=\psi(x,y)$. Podemos formar el sistema
$$\begin{matrix}G(x,y,u,v)=u-\varphi(x,y)\\H(x,y,u,v)=v-\psi(x,y)\end{matrix}$$
se tiene entonces que

$$\frac{\partial (G,H)}{\partial (x,y)}=\left|\begin{matrix}
\frac{\partial G}{\partial x} & \frac{\partial G}{\partial y} \\
\frac{\partial H}{\partial x} & \frac{\partial H}{\partial y}
\end{matrix}\right|$$

$$=\left|\begin{matrix}
-\frac{\partial \varphi}{\partial x} & -\frac{\partial \varphi}{\partial y} \\
-\frac{\partial \psi}{\partial x} & -\frac{\partial \psi}{\partial y}
\end{matrix}\right|$$
$$=\left|\begin{matrix}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\
\frac{\partial v}{\partial x} &\frac{\partial v}{\partial y}
\end{matrix}\right|$$
$$
JF^{-1}=\left[\begin{array}{cc}
\displaystyle\frac{\partial u}{\partial x} & \displaystyle\frac{\partial u}{\partial y}\\
\displaystyle\frac{\partial v}{\partial x} & \displaystyle\frac{\partial v}{\partial y} \end{array} \right]
$$

El resultado anterior $\ast$ nos dice como calcular las derivadas parciales $\displaystyle\frac{\partial u}{\partial x}$, $\displaystyle\frac{\partial u}{\partial y}$, $\displaystyle\frac{\partial v}{\partial x}$, $\displaystyle\frac{\partial v}{\partial y}$ en una vecindad $V$ de $(x,y)$ al sustituir las fórmulas correspondientes en $JF^{-1}$, recordando que $\displaystyle\frac{\partial(f,g)}{\partial(u,v)}= det(JF)$.

$$ JF^{-1}= \left|\begin{array}{cc}
\displaystyle\frac{\displaystyle\frac{\partial g}{\partial v}}{det(JF)} & -\displaystyle\frac{\displaystyle\frac{\partial g}{\partial u}}{det(JF)}\\
-\displaystyle\frac{\displaystyle\frac{\partial f}{\partial v}}{det(JF)} & \displaystyle\frac{\displaystyle\frac{\partial f}{\partial U}}{det(JF)}\end{array}\right|=\displaystyle\frac{1}{det(JF)} \left|\begin{array}{cc}
\displaystyle\frac{\partial g}{\partial v} & -\displaystyle\frac{\partial f}{\partial v}\\
-\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial f}{\partial u} \end{array}\right|
$$

Multipliquemos $JF$ y $JF^{-1}$, se obtiene

$$
(JF)(JF^{-1})= \left|\begin{array}{cc}
\displaystyle\frac{\partial f}{\partial u} & \displaystyle\frac{\partial f}{\partial v}\\
\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial g}{\partial v} \end{array}\right| \displaystyle\frac{1}{det(JF)}\left[\begin{array}{cc}
\displaystyle\frac{\partial g}{\partial v} & -\displaystyle\frac{\partial f}{\partial v}\\
-\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial f}{\partial u} \end{array}\right]= \displaystyle\frac{1}{det(JF)}\left|\begin{array}{cc}
\displaystyle\frac{\partial f}{\partial u} & \displaystyle\frac{\partial f}{\partial v}\\
\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial g}{\partial v} \end{array}\right| \left|\begin{array}{cc}
\displaystyle\frac{\partial g}{\partial v} & -\displaystyle\frac{\partial f}{\partial v}\\
-\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial f}{\partial u} \end{array}\right|
$$

$$= \displaystyle\frac{1}{det(JF)}\left|\begin{array}{cc} \displaystyle\frac{\partial f}{\partial u} \displaystyle\frac{\partial g}{\partial v} – \displaystyle\frac{\partial f}{\partial v} \displaystyle\frac{\partial g}{\partial u} & 0 \\
0& -\displaystyle\frac{\partial g}{\partial u} \displaystyle\frac{\partial f}{\partial v} + \displaystyle\frac{\partial g}{\partial v} \displaystyle\frac{\partial f}{\partial u} \end{array}\right|=\displaystyle\frac{\displaystyle\frac{\partial f}{\partial u}\displaystyle\frac{\partial g}{\partial v} – \displaystyle\frac{\partial f}{\partial v}\displaystyle\frac{\partial g}{\partial u}}{det(JF)}\left[\begin{array}{cc}
1 & 0\\
0 & 1 \end{array}\right] = \left[\begin{array}{cc}
1 & 0\\
0 & 1 \end{array}\right]
$$

Así concluimos que la matriz jacobiana de la función inversa de F es justamente la inversa de la matriz jacobiana de F. Es decir se tiene
$$JF^{-1}=(JF)^{-1}$$

$\textbf{Ejemplo.}$

Considere las ecuaciones dadas por $x=u^2+v^3,~~y=u^2+uv$. Se tiene
que en $p=(1,2)$ $x=9,~y=3$.\
Las derivadas parciales de las funciones
$x=f(u,v)=u^3+v^3$ , $y=g(u,v)=u^2+uv$ son
$$
\displaystyle\frac{\partial f}{\partial u}=3u^2~,~ \displaystyle\frac{\partial f}{\partial v}=3v^2 ~,~ \displaystyle\frac{\partial g}{\partial u}=2u+v ~,~\displaystyle\frac{\partial g}{\partial v}=u
$$

La matriz jacobiana de f es
$$JF=\left|\begin{array}{cc}
\displaystyle\frac{\partial f}{\partial u} & \displaystyle\frac{\partial f}{\partial v}\\
\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial g}{\partial v} \end{array}\right|=\left|\begin{array}{cc}
3u^2 & 3v^2\
2u+v & u \end{array}\right|
$$
la cual en el punto $(1,2)$ es invertible pues
$$ detJF(1,2) = \left|\begin{array}{cc}
3 & 12\
4 & 1 \end{array}\right| = -45\neq0
$$

Así podemos concluir que en una bola $B’$ de $(9,3)$ se da la inversa $F^{-1}$ de $F$ o bien, que podemos despejar de $x=u^3+v^3 , y=u^2+uv$ a $u,v$ como funciones de $x$ e $y$, la cual es de clase $C^1$ en $B’$ y que su derivada es
$$JF^{-1}(x,y)= [JF(u,v)]^{-1}=\displaystyle\frac{1}{detJF} \left[\begin{array}{cc}
\displaystyle\frac{\partial g}{\partial v} & -\displaystyle\frac{\partial f}{\partial v}\\
-\displaystyle\frac{\partial g}{\partial u} & \displaystyle\frac{\partial f}{\partial u} \end{array}\right]=\displaystyle\frac{1}{3u^3-6uv^2-3v^3} \left|\begin{array}{cc}
u & -3v^2\
-(2u+v) & 3u^2 \end{array}\right|
$$
donde $x=u^3+v^3 , y=u^2+uv$. Es decir

$$\displaystyle\frac{\partial u}{\partial x}(u^3+v^3, u^2+uv)= \displaystyle\frac{u}{3u^3-6uv^2-3v^3}$$
$$\displaystyle\frac{\partial u}{\partial y}(u^3+v^3, u^2+uv)= \displaystyle\frac{-3v^2}{3u^3-6uv^2-3v^3}$$
$$\displaystyle\frac{\partial u}{\partial y}(u^3+v^3, u^2+uv)= \displaystyle\frac{-2u+v}{3u^3-6uv^2-3v^3}$$
$$\displaystyle\frac{\partial u}{\partial y}(u^3+v^3, u^2+uv)= \displaystyle\frac{3u^2}{3u^3-6uv^2-3v^3}$$

Considere las ecuaciones
$$x=u+v+e^{w}$$
$$y=u+w+e^{2v}$$
$$x=v+w+e^{3u}$$
para $p=(u,v,w)=(0,0,0)$ se tiene que $q=(x,y,z)=(1,1,1)$ el
determinante de la matriz jacobiana de la función $F(u,v,w))(x,y,z)$
es:

$$
det
JF=\frac{\partial(x,y,z)}{\partial(u,v,w)}=\left|\begin{array}{ccc}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\
\frac{\partial y}{\partial u} & \frac{\partial x}{\partial v} &
\frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} &
\frac{\partial z}{\partial v} & \frac{\partial z}{\partial
w}\end{array}\right|=\left|\begin{array}{ccc}
1 & 1 & e^{w}\\
1 & 2e^{2v} & 1\\ 3e^{3u} & 1 &
1\end{array}\right|_{(0,0,0)}=\left|\begin{array}{ccc}
1& 1 &1\\
1 & 2 &1\\3 & 1 & 1\end{array}\right|
$$

Si calculamos su determinante obtenemos

$$=\left|\begin{array}{ccc}
\textcolor{Green}{1}&\textcolor{Red} {1} &\textcolor{Blue}{1}\\
1 & 2 &1\\ 3 & 1 & 1\end{array}\right|=\textcolor{Green}{1\times
\left|\begin{array}{cc}
2 & 1 \\
1 & 1\end{array}\right|}-\textcolor{Red}{1\times
\left|\begin{array}{cc}
1 & 1 \\
3 & 1\end{array}\right|}+\textcolor{Blue}{1\times
\left|\begin{array}{cc}
1 & 2 \\
3 & 1
1\end{array}\right|}=\textcolor{Green}{1\times(2-1)}-\textcolor{Red}{1\times(1-3)}+\textcolor{Blue}{1\times(1-6)}=\textcolor{Green}{1}+\textcolor{Red}{2}-\textcolor{Blue}{5}=-2\neq
0$$

$\therefore$ Podemos localmente invertir la función $F$, entorno al punto $q$, donde podemos definir funciones de clase

$c^{1}$ $u(x,y,z), v(x,y,z)$ y $w(x,y,z)$. Ahora bien como $$JF^{-1}(q)=\left[JF(p)\right]^{-1}=\left|\begin{array}{ccc}
1& 1 &1\\
1 & 2 &1\\3 & 1 &
1\end{array}\right|^{-1}\underbrace{=}_{*}\left|\begin{array}{ccc}
-\frac{1}{2}& 0 &\frac{1}{2}\\
-1 & 1 &0\\ \frac{5}{2} & -1 & -\frac{1}{2}\end{array}\right|$$

• Vamos a calcular la inversa usando la matriz de cofactores de la matriz $\left(\begin{array}{ccc}
  \textcolor{OliveGreen}{1}&\textcolor{Magenta} {1} &\textcolor{Violet}{1}\\
  \textcolor{Brown}{1} &\textcolor{Orange} {2}
  &\textcolor{Blue}{1}\\ \textcolor{RedViolet}{3} &
  \textcolor{Fuchsia}{1} &\textcolor{Emerald} {1}\end{array}\right)$

$$\left(\begin{array}{ccc}
\textcolor{OliveGreen}{(-1)^{1+1}\times \left|\begin{array}{cc}
2 & 1 \\
1 & 1\end{array}\right|}&\textcolor{Magenta} {(-1)^{1+2}\times
\left|\begin{array}{cc}
1 & 1 \\
3 & 1\end{array}\right|} &\textcolor{Violet}{(-1)^{1+3}\times
\left|\begin{array}{cc}
1 & 2 \\
3 & 1
1\end{array}\right|}\\
\textcolor{Brown}{(-1)^{2+1}\times \left|\begin{array}{cc}
1 & 1 \\
1 & 1\end{array}\right|} &\textcolor{Orange} {(1)^{2+2}\times
\left|\begin{array}{cc}
1 & 1 \\
3 & 1\end{array}\right|} &\textcolor{Blue}{(-1)^{2+3}\times
\left|\begin{array}{cc}
1 & 1 \\
3 & 1\end{array}\right|}\\ \textcolor{RedViolet}{(-1)^{3+1}\times
\left|\begin{array}{cc}
1 & 1 \\
2 & 1\end{array}\right|} & \textcolor{Fuchsia}{(-1)^{3+2}\times
\left|\begin{array}{cc}
1 & 1 \\
1 & 1\end{array}\right|} &\textcolor{Emerald} {(1)^{3+3}\times
\left|\begin{array}{cc}
1 & 1 \\
1 & 2\end{array}\right|}\end{array}\right)=\left(\begin{array}{ccc}
\textcolor{OliveGreen}{1}&\textcolor{Magenta} {2} &\textcolor{Violet}{-5}\\
\textcolor{Brown}{0} &\textcolor{Orange} {-2}
&\textcolor{Blue}{2}\\\textcolor{RedViolet}{-1} &
\textcolor{Fuchsia}{0} &\textcolor{Emerald} {1}\end{array}\right)$$

Transponiendo la ultima matriz tenemos
$$\left(\begin{array}{ccc}
\textcolor{OliveGreen}{1}&\textcolor{Brown} {0} &\textcolor{RedViolet}{-1}\\
\textcolor{Magenta}{2} &\textcolor{Orange} {-2}
&\textcolor{Fuchsia}{0}\\ \textcolor{Violet}{-5} &
\textcolor{Blue}{2} &\textcolor{Emerald} {1}\end{array}\right)$$
$\therefore$

$$\left|\begin{array}{ccc}
1& 1 &1\\
1 & 2 &1\\ 3 & 1 & 1\end{array}\right|^{-1}=\frac{1}{-2}\times
\left(\begin{array}{ccc}
\textcolor{OliveGreen}{1}&\textcolor{Brown} {0} &\textcolor{RedViolet}{-1}\\
\textcolor{Magenta}{2} &\textcolor{Orange} {-2}
&\textcolor{Fuchsia}{0}\\ \textcolor{Violet}{-5} &
\textcolor{Blue}{2} &\textcolor{Emerald}
{1}\end{array}\right)=\left(\begin{array}{ccc}
\textcolor{OliveGreen}{-\frac{1}{2}}&\textcolor{Brown} {0} &\textcolor{RedViolet}{\frac{1}{2}}\\
\textcolor{Magenta}{-1} &\textcolor{Orange} {1}
&\textcolor{Fuchsia}{0}\\textcolor{Violet}{\frac{5}{2}} &
\textcolor{Blue}{-1} &\textcolor{Emerald}
{-\frac{1}{2}}\end{array}\right)$$ $\therefore$ las parciales son:
$$\frac{\partial u}{\partial x}(q)=-\frac{1}{2}\quad \frac{\partial u}{\partial y}(q)=0\quad \frac{\partial u}{\partial z}(q)=\frac{1}{2}$$
$$\frac{\partial v}{\partial x}(q)=-1\quad \frac{\partial v}{\partial y}(q)=1\quad \frac{\partial v}{\partial z}(q)=0$$
$$\frac{\partial w}{\partial x}(q)=\frac{5}{2}\quad \frac{\partial w}{\partial y}(q)=-1\quad \frac{\partial w}{\partial z}(q)=-\frac{1}{2}$$

Introducción

El propósito de esta entrada será conocer criterios para determinar cuándo el límite de una sucesión de funciones es una función continua. (El concepto de función continua se vio en la entrada Funciones continuas en espacios métricos).

Nuestra intuición podría proponer que esto ocurre cuando todas las funciones de la sucesión son también continuas. No obstante, esto no basta cuando el límite de convergencia es puntual. Como ejemplo tomemos la sucesión de funciones continuas dada por:

$(x^n)_{n \in \mathbb{N}}$ donde para cada $n \in \mathbb{N}, \, x^n:[0,1] \to \mathbb{R}$

Queda como ejercicio al lector demostrar que $(x^n)_{n \in \mathbb{N}}$ converge puntualmente a la función:

\begin{equation*}
f(x) = \begin{cases}
0 & \text{si $0 \leq x < 1$} \\
1 & \text{si $x = 1$}
\end{cases}
\end{equation*}

Pero $f$ no es una función continua en $[0,1].$

¿Qué ocurre en los casos donde el límite es uniforme? A continuación mostraremos que bajo esa situación, la función a la que la sucesión converge sí es continua. Pero antes hagamos una aclaración sobre la notación a usar:

En la entrada anterior (Convergencia puntual y convergencia uniforme) las funciones suelen definirse como funciones de $A$ en $X$ $(f:A \to X),$ donde $A$ se considera como un conjunto cualquiera (que no necesariamente es un espacio métrico y por tanto la distancia de los puntos en el dominio no es relevante), y $X$ es un espacio métrico con distancia indicada como $d$.

Ahora pasamos a tratar con funciones continuas, donde sí comparamos distancias entre puntos del dominio (la famosa distancia menor que $\delta$) y distancias en puntos del contradominio (la famosa distancia menor que $\varepsilon$). Así, las funciones de esta entrada están definidas entre dos espacios métricos $(X,d_X)$ y $(Y,d_Y).$ Nota la importancia de señalar si la distancia a considerar es en $X$ o en $Y.$

Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Si $(f_n)_{n \in \mathbb{N}}$ con $f_n: X \to Y, \, n \in \mathbb{N} \, $ es una sucesión de funciones continuas que converge uniformemente a $f:X \to Y$ en $X$ entonces $f$ es continua.

Demostración:
Sea $\varepsilon > 0$ y $x_0 \in X.$ Buscamos probar que $f$ es continua en $x_0.$ Como $(f_n)_{n \in \mathbb{N}}$ converge uniformemente en $f$ entonces existe $N \in \mathbb{N}$ tal que para todo $k \geq N$ y para todo $x \in X, \, d_Y(f_k(x),f(x)) < \frac{\varepsilon}{3}.$

Por otro lado, como $f_N$ es continua, existe $\delta > 0$ tal que si $d_X(x,x_0)< \delta$ entonces $d_Y(f_N(x),f_N(x_0)) < \frac{\varepsilon}{3}.$

En consecuencia, si $d_X(x,x_0)< \delta$ se sigue que

\begin{align*}
d_Y(f(x),f(x_0)) & \leq d_Y(f(x),f_N(x)) + d_Y(f_N(x),f_N(x_0)) + d_Y(f_N(x_0),f(x_0)) \\
& < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} \\
& = \varepsilon
\end{align*}

Lo cual demuestra que el límite uniforme de una sucesión de funciones continuas, es una función continua.

Es importante notar que esto no significa que toda sucesión de funciones continuas que converge en una función continua, lo hace de manera uniforme. Puede hacerlo solo de forma puntual. Veamos un ejemplo.

Ahora pensemos en funciones continuas y acotadas a través de la siguiente definición. (El concepto de función acotada se vio en Espacios de funciones).

Definición. El espacio métrico $\mathcal{C}_b^0(X,Y)$: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. El espacio de funciones continuas y acotadas de $X$ a $Y$ se define como:
$\mathcal{C}_b^0(X,Y):= \{f:X \to Y: f \text{ es continua y acotada } \}$
Y la métrica está dada por:
$$d_\infty(f,g)= \underset {x \in X}{sup} \, \, d_Y(f(x),g(x))$$

Donde $f,g \in \mathcal{C}_b^0(X,Y).$

Este espacio es cerrado en el espacio de funciones acotadas, de acuerdo con la siguiente:

Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Entonces $\mathcal{C}_b ^0(X,Y)$ es un subespacio cerrado de $\mathcal{B}(X,Y).$ (El espacio de funciones acotadas).

Demostración:
Buscamos probar que $\mathcal{C}_b ^0(X,Y)$ es igual a su cerradura. Sea $f \in \overline{\mathcal{C}_b ^0(X,Y)}.$ En la última proposición de la entrada Convergencia vimos que esto significa que existe una sucesión de funciones $(f_n)_{n \in \mathbb{N}}$ en $\mathcal{C}_b ^0(X,Y)$ que convergen a $f$ en $\mathcal{B}(X,Y).$ En la entrada anterior vimos que esto implica que $f$ es límite uniforme de $(f_n)_{n \in \mathbb{N}}. \, $ La proposición anterior nos permite concluir que $f$ es continua, es decir $f \in \mathcal{C}_b ^0(X,Y),$ probando así que $\mathcal{C}_b ^0(X,Y)$ es cerrado en $\mathcal{B}(X,Y).$

Ahora veamos la siguiente:

Proposición: Sea $Y$ un espacio métrico completo. Se cumple que:

1. Si $A$ es un conjunto entonces $\mathcal{B}(A,Y)$ es completo.
2. Si $X$ un espacio métrico entonces $\mathcal{C}^0_b(X,Y)$ es completo.

Demostración:
Para probar que $\mathcal{B}(A,Y)$ es completo toma $(f_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $\mathcal{B}(A,Y).$ Veamos que es convergente.
Sea $\varepsilon >0.$ Por definición, existe $N \in \mathbb{N}$ tal que $\forall \, l,m \geq N, \, d_\infty(f_l,f_m) < \varepsilon.$ Así, para cada $a \in A$ se cumple que $d_Y(f_l(a),f_m(a)) \leq d_\infty(f_l,f_m) < \varepsilon$ de modo que $(f_n)_{n \in \mathbb{N}}$ es uniformemente de Cauchy. De acuerdo con el Criterio de convergencia uniforme de Cauchy visto en la entrada anterior esto significa que $(f_n)_{n \in \mathbb{N}}$ converge uniformemente en $A$ y por tanto converge en el espacio métrico de funciones $\mathcal{B}(A,Y).$

Para probar que $\mathcal{C}^0_b(X,Y)$ es completo partimos de la proposición anterior donde concluimos que es subespacio cerrado de $\mathcal{B}(A,Y)$ que ya sabemos es completo. A partir de una proposición vista en Espacios métricos completos se sigue que $\mathcal{C}^0_b(X,Y)$ es completo.

Si $Y$ es un espacio de Banach entonces está provisto de una norma $\norm{\cdot}$ que induce una métrica bajo la cual $Y$ es completo.

Al final se te pedirá probar que el conjunto $\mathcal{B}(A,Y)$ es un espacio vectorial normado con
$\norm{f}_\infty = \underset {a \in A}{sup} \, \norm{f(a)}$

En esta situación, las proposiciones se plantean de la siguiente manera:

1. Si $A$ es un conjunto entonces $\mathcal{B}(A,Y)$ es de Banach.
2. Si $X$ un espacio métrico entonces $\mathcal{C}^0_b(X,Y)$ es de Banach.

Unos resultados que requieren el concepto de compacidad

En entradas posteriores hablaremos del concepto de espacios métricos compactos. En la sección Funciones en espacios topológicos compactos verás que toda función continua en un compacto es acotada. Ese resultado en suma con la proposición anterior, permite concluir que si $A$ es compacto y $X$ es completo entonces $\mathcal{C}^0(A,X)=\{\phi:A \to X :\phi \text{ es continua } \}$ es un espacio completo.

Ahora presentamos condiciones que aseguran la convergencia uniforme de una sucesión de funciones continuas en un espacio compacto a partir de la monotonía. Es decir:

Proposición: Sea $A$ un espacio métrico compacto, $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones continuas con $f_n:A \to \mathbb{R}, n \in \mathbb{N}$ tal que $(f_n)$ converge puntualmente a una función continua $f$. Si para cada $x \in A$ y $n \in \mathbb{N} \, f_n(x) \geq f_{n+1}(x),$ entonces $(f_n)$ converge a $f$ uniformemente en $A.$

Demostración:
Podrá consultarse en la entrada Compacidad en espacios métricos.

Más adelante…

Continuaremos analizando resultados de convergencia uniforme, ahora en funciones diferenciables. ¿Será diferenciable también la función límite? ¿Será convergente también la sucesión de derivadas? ¿Coincide el límite de derivadas con la derivada de la función límite?

Tarea moral

1. Demuestra que $(x^n)_{n \in \mathbb{N}}$ con $x^n:[0,1] \to \mathbb{R}$ converge puntualmente a la función:
   \begin{equation*}
   f(x) = \begin{cases}
   0 & \text{si $0 \leq x < 1$} \\
   1 & \text{si $x = 1$}
   \end{cases}
   \end{equation*}
   Pero $f$ no es una función continua en $[0,1].$
2. Demuestra que la sucesión de funciones continuas $(f_n)_{n \in \mathbb{N}}$ donde para cada $n \in \mathbb{N}, \, f_n:[0,1] \to \mathbb{R}$ se define como $f_n(x)= n^2x(1-x)^n,$ converge de forma puntual a la función $f(x)=0$ pero el límite no es uniforme.
3. Sea $A$ un conjunto, y $(Y, \norm{\cdot})$ un espacio normado. Prueba que $\mathcal{B}(A,Y)$ es un espacio vectorial con las operaciones
   $(f+g)(x):= f(x) + g(x)$
   $(\lambda f)(x):= \lambda f(x)$
   Y que $\norm{f}_\infty = \underset {a \in A}{sup} \, \norm{f(a)}$
   es una norma en $\mathcal{B}(A,Y).$

Enlaces:

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

$\textcolor{Red}{\textbf{Teorema de la Función Implícita (sistemas de ecuaciones)}}$

$\textbf{Teorema 1.}$ Considere las funciones $z_{1}=F(x,y,u,v)$ y $z_{2}=G(x,y,u,v)$. Sea $P=(x,y,u,v) \in \mathbb{R}^{4}$ un punto tal que $F(P)=G(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{4}$ de centro $P$ las funciones $F$ y $G$ tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano $\displaystyle \frac{\partial
(F,G)}{\partial (u,v)}(P)\neq0$ entonces las expresiones $F(x,y,u,v)=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas) $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ definidas en una vecindad $v$ de $(x,y)$ las cuales tienen derivadas parciales continuas en $v$

Dadas las funciones $F$ y $G$ de las variables $u,v,x,y$ nos preguntamos cuando de las expresiones

$F(x,y,u,v)=0$
$G(x,y,u,v)=0$

podemos despejar a $u$ y $v$ en términos de $x$ y $y$ en caso de ser posible diremos que las funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ son funciones implícitas dadas. Se espera que $\exists’$n funciones $u=\varphi_{1}(x,y)$ y
$v=\varphi_{2}(x,y)$ en

$F(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$
$G(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$

con $(x,y)$ en alguna vecindad $V$

Suponiendo que existen $\varphi_{1}$ y $\varphi_{2}$ veamos sus derivadas

$\displaystyle \frac{\partial F}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial F}{\partial y}\displaystyle \frac{\partial y}{\partial x}+\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial
x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial F}{\partial u}\displaystyle
\frac{\partial u}{\partial x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial F}{\partial x}$

$\displaystyle \frac{\partial G}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial G}{\partial y}\displaystyle \frac{\partial y}{\partial
x}+\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial G}{\partial x}$

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas $\displaystyle \frac{\partial u}{\partial x}$ y $\displaystyle \frac{\partial v}{\partial x}$. Aquí se ve que para que el sistema tenga solución.

$det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq0$ en $(P)$ (el $det$ Jacobiano) y según la regla de Cramer

$\displaystyle \frac{\partial u}{\partial x}=\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
x}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial x}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{\det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(x,v)}}{\frac{\partial(F,G)}{\partial(u,v)}}$, $\displaystyle \frac{\partial
v}{\partial x}=\frac{\det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle -\frac{\partial
F}{\partial x}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial
x}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(u,x)}}{\frac{\partial(F,G)}{\partial(u,v)}}$.

Análogamente si derivamos con respecto a $y$ obtenemos

$\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial y}=\displaystyle \frac{\partial F}{\partial y}$

$\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=\displaystyle \frac{\partial G}{\partial y}$

de donde

$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
y}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial y}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(y,v)}}{\frac{\partial(F,G)}{\partial(u,v)}}$, $\displaystyle \frac{\partial
v}{\partial y}=-\frac{\det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle -\frac{\partial
F}{\partial y}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial
y}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(u,y)}}{\frac{\partial(F,G)}{\partial(u,v)}}$.

Al determinante $det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle \frac{\partial
F}{\partial v}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|$ lo llamamos Jacobiano y lo denotamos por $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}$.

$\textbf{Ejemplo.}$ Analizar la solubilidad del sistema
$$e^{u}+e^{v}=x+ye$$
$$ue^{u}+ve^{v}=xye$$
$\small{Solución}$ En este caso definimos
$$F(x,y,u,v)=e^{u}+e^{v}-x-ye=0$$
$$G(x,y,u,v)=ue^{u}+ve^{v}-xye=0$$
por lo que el sistema tendra solución si $\displaystyle{\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}\neq 0$

En este caso
$$\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|=\det\left|\begin{array}{cc} \displaystyle e^{u}&\displaystyle e^{v}\\ue^{u}+e^{e^{u}}&ve^{v}+e^{v}\end{array}\right|=e^{u}\left(ve^{v}+e^{v}\right)-e^{v}\left(ue^{u}+e^{u}\right)=ve^{u+v}-ue^{v+u}\neq 0$$
por lo tanto u y v se pueden ver en términos de x,y $\therefore$ se pueden calcular sus parciales en $u=0,~v=1,~x=1, ~y=1$ que es este caso dan
$$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{matrix}-1&-ye\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-(ve^{v}+e^{v})+e^{v}ye}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{2e-e^{2}}{e}=2-e$$ $$\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-1&-ye\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-ye^{u}e+ue^{u}+e^{u}}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e-1}{e}=1-e^{-1}$$
$$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{matrix}-e&-xe\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e(ve^{v}+e^{v})+e^{v}xe}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e^{2}+e^{2}-e^{2}}{e}=e$$ $$\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-e&-xe\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e^{u}xe+e(ue^{u}+e^{u})}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e-e}{e}=0$$

$\textcolor{Red}{\textbf{Teorema de la Función Implícita (n-sistemas de ecuaciones)}}$

Considere las n-funciones
$$u_{i}=F_{i}(x_{1},…,x_{m},y_{1},…,y_{n}),~i=1,…,n$$ Sea $P=(\overline{x}{1},…,\overline{x}{m},\overline{y}{1},…,\overline{y}{n}) \in \mathbb{R}^{n+m}$ un punto tal que $F_{i}(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{n+m}$ de centro $P$ las funciones $F_{i}$ tienen (sus $m+n$) derivadas parciales continuas. Si el Jacobiano $$ \frac{\partial(F_{1},F_{2},…,F_{n})}{\partial (y_{1},y_{2},…,y_{n})}=\left|\begin{matrix}\frac{\partial F_{1}}{\partial y_{1}}&\frac{\partial F_{1}}{\partial y_{2}}&\cdots&\frac{\partial F_{1}}{\partial y_{n}}\\ \frac{\partial F_{2}}{\partial y_{1}}&\frac{\partial F_{2}}{\partial y_{2}}&\cdots&\frac{\partial F_{2}}{\partial y_{n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial F_{n}}{\partial y_{1}}&\frac{\partial F_{n}}{\partial y_{2}}&\cdots&\frac{\partial F_{n}}{\partial y_{n}} \end{matrix}\right|\neq0~en~~P$$

entonces las expresiones
$F_{i}(x_{1},…,x_{m},y_{1},…,y_{n})=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas)
$y_{i}=\varphi_{i}(x_{1},…,x_{m}),~i=1,…,n$ definidas en una vecindad $v$ de $(\overline{x}{1},…,\overline{x}{m})$ las cuales tienen derivadas parciales
continuas en $v$ que se pueden calcular como
$$\frac{\partial y_{i}}{\partial x_{j}}=\frac{\frac{\partial(F_{1},F_{2},…,F_{n})}{\partial (y_{1},…,y_{i-1},x_{j},y_{i+1},…,y_{n})}}{\frac{\partial (F_{1},F_{2},…,F_{n})}{\partial (y_{1},y_{2},…,y_{n})}}$$

$\textbf{Ejemplo.}$ Considere las ecuaciones
$$\begin{matrix}
F(x,y,u,v,w)=x+y+u+v+w=0 \\
G(x,y,u,v,w)=x^{2}-y^{2}+u^{2}-2v^{2}+w^{2}+1=0 \\
H(x,y,u,v,w)=x^{3}+y^{3}+u^{4}-3v^{4}+8w^{4}+2=0
\end{matrix}$$

En el punto $P=(1,-1,1,-1,0)$, se tiene $F(P)=G(P)=H(P)=0$. Todas las derivadas parciales de F, G, H son continuas. Se tiene además que
$$\frac{\partial (F,G,H)}{\partial (u,v,w)}=\det\left|\begin{matrix}1&1&1\\ 2u&-4v&2w\\ 4u^{3}&-12v^{3}&32w^{2}\end{matrix}\right|_{\begin{matrix}u=1\\ v=-1\\ w=0\end{matrix}}=8\neq 0$$
Entonces el teorema asegura que en torno a P podemos despejar $u,v,w$ en términos de $x,y$ y establecer funciones
$$u=u(x,y),~v=v(x,y),~w=w(x,y)$$
las cuales tienen derivadas parciales continuas en una vecindad de $(1,-1)$ que se pueden calcular

$$\frac{\partial u}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (x,v,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},\frac{\partial u}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (y,v,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

$$\frac{\partial v}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (u,x,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},\frac{\partial v}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (u,y,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

$$\frac{\partial w}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (u,v,x)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},~~\frac{\partial w}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (u,v,y)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

$\textcolor{Red}{\textbf{Teorema de la Función Implícita ($f:\mathbb{R}\rightarrow\mathbb{R}$)}}$

$\textbf{Teorema.}$ Considere la función $y=f(x)$. Sea $(x_{0},y_{0}) \in \mathbb{R}^{2}$ un punto tal que $F(x_{0},y_{0})=0$. Suponga que la función $F$ tiene derivadas parciales continuas en alguna bola con centro $(x_{0},y_{0})$ y que $\displaystyle \frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$. Entonces $F(x,y)=0$ se puede resolver para $y$ en términos de $x$ y definir así una función $y=f(x)$ con dominio en una vecindad de $(x_{0},y_{0})$, tal que $y_{0}=f(x_{0})$, lo cual tiene derivadas continuas en $\mathcal{V}$ que pueden calcularse como $y’=f'(x)= \displaystyle \frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$, $x \in \mathcal{V}$.

$\textbf{Ejercicio}$ Si $$y’=f'(x)=-\displaystyle \frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$$ calcular $y^{»}$

$\small{Solución}$ En este caso
$$y^{»}=-\frac{\left(\frac{\partial F}{\partial y}\right)\left[\frac{\partial^{2} F}{\partial x^{2}}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y\partial x}\frac{dy}{dx}\right]-\left(\frac{\partial F}{\partial x}\right)\left[\frac{\partial^{2} F}{\partial x\partial y}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y^{2}}\frac{dy}{dx}\right]}{\left(\frac{\partial F}{\partial y}\right)^{2}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)\left[\frac{\partial^{2} F}{\partial x^{2}}+\frac{\partial^{2} F}{\partial y\partial x}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}\right)\right]-\left(\frac{\partial F}{\partial x}\right)\left[\frac{\partial^{2} F}{\partial x\partial y}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y^{2}}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}\right)\right]}{\left(\frac{\partial F}{\partial y}\right)^{2}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)^{2}\left(\frac{\partial^{2} F}{\partial x^{2}}\right)-\left(\frac{\partial^{2} F}{\partial y\partial x}\right)\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)-\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)\left(\frac{\partial^{2} F}{\partial x\partial y}\right)+\left(\frac{\partial F}{\partial x}\right)^{2}\left(\frac{\partial^{2} F}{\partial y^{2}}\right)}{\left(\frac{\partial F}{\partial y}\right)^{3}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)^{2}\left(\frac{\partial^{2} F}{\partial x^{2}}\right)-2\left(\frac{\partial^{2} F}{\partial y\partial x}\right)\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)+\left(\frac{\partial F}{\partial x}\right)^{2}\left(\frac{\partial^{2} F}{\partial y^{2}}\right)}{\left(\frac{\partial F}{\partial y}\right)^{3}}$$

$\textcolor{Red}{\textbf{Teorema de la Función Implícita ($f:\mathbb{R}^{2}\rightarrow\mathbb{R}$)}}$

$\textbf{Teorema}$ Considere la función $F(x,y,z)$. Sea $(x_{0},y_{0},z_{0}) \in
\mathbb{R}^{3}$ un punto tal que $F(x_{0},y_{0},z_{0})=0$. Suponga que la
función F tiene derivadas parciales $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y},~\frac{\partial F}{\partial z}}$ continuas en alguna bola con
centro $(x_{0},y_{0},z_{0})$ y que $\displaystyle \frac{\partial
F}{\partial z}(x_{0},y_{0},z_{0})\neq 0$.
Entonces $F(x,y,z)=0$ se puede resolver para $z$ en términos de $x,y$
y definir así una función $z=f(x,y)$ con dominio en una vecindad de
$(x_{0},y_{0},z_{0})$, tal que $z_{0}=f(x_{0},y_{0})$, lo cual tiene derivadas continuas
en $\mathcal{V}$ que pueden calcularse como $$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}~~~\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$

$\textbf{Ejercicio}$ Si
$$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$ calcular $$\frac{\partial^{2}F}{\partial x^{2}}$$

$\small{Solución}$ Tenemos que
$$\frac{\partial^{2}F}{\partial x^{2}}=\frac{\partial}{\partial x}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}\right)=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}} \frac{dx}{d x}+ \frac{\partial^{2} F}{\partial y\partial x} \frac{dy}{dx}+ \frac{\partial^{2} F}{\partial z\partial x} \frac{dz}{dx}\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}\frac{dx}{d x}+ \frac{\partial^{2} F}{\partial y\partial z} \frac{dy}{dx}+ \frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dx}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}}+ \frac{\partial^{2} F}{\partial z\partial x} \frac{dz}{dx}\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}+\frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dx}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}}+ \frac{\partial^{2} F}{\partial z\partial x} \left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}\right)\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}+\frac{\partial^{2} F}{\partial z^{2}}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial x^{2}}-2 \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial F}{\partial x}\frac{\partial F}{\partial z}+\left(\frac{\partial F}{\partial x}\right)^{2}{\frac{\partial^{2} F}{\partial z^{2}}}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

$\textbf{Ejercicio}$ Si
$$\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$ calcular $$\frac{\partial^{2}F}{\partial y^{2}}$$

$\small{Solución}$ tenemos que
$$\frac{\partial^{2}F}{\partial y^{2}}=\frac{\partial}{\partial y}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}\right)=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} \frac{dx}{d y}+ \frac{\partial^{2} F}{\partial y^{2}} \frac{dy}{dy}+ \frac{\partial^{2} F}{\partial z\partial y} \frac{dz}{dy}\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}\frac{dx}{d y}+ \frac{\partial^{2} F}{\partial y\partial z} \frac{dy}{dy}+ \frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dy}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y^{2}}+ \frac{\partial^{2} F}{\partial z\partial y} \frac{dz}{dy}\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial y \partial z}+\frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dy}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y^{2}}+ \frac{\partial^{2} F}{\partial z\partial y} \left(-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}\right)\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial y \partial z}+\frac{\partial^{2} F}{\partial z^{2}}\left(-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial y^{2}}-2 \frac{\partial^{2} F}{\partial z\partial y} \frac{\partial F}{\partial y}\frac{\partial F}{\partial z}+\left(\frac{\partial F}{\partial y}\right)^{2}{\frac{\partial^{2} F}{\partial z^{2}}}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

$\textbf{Ejercicio}$ Si
$$\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}$$ calcular $$\frac{\partial^{2}F}{\partial y\partial x}$$

$\small{Solución}$ tenemos que
$$\frac{\partial^{2}F}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial F}{\partial x}\right)=\frac{\partial}{\partial y}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}}{\displaystyle \frac{\partial F}{\partial z}}\right)=$$
$$-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} + \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial z}{\partial y}\right]-\left(\frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial y\partial z} +\frac{\partial^{2} F}{\partial z^{2}}\frac{\partial z}{\partial y}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} + \frac{\partial^{2} F}{\partial z\partial x} \left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}\right)\right]-\left(\frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial y\partial z} +\frac{\partial^{2} F}{\partial z^{2}}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial y\partial x}- \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial F}{\partial y}\frac{\partial F}{\partial z}-\frac{\partial^{2} F}{\partial y\partial z} \frac{\partial F}{\partial x}\frac{\partial F}{\partial z}+\frac{\partial^{2} F}{\partial z^{2}}\frac{\partial F}{\partial x}\frac{\partial F}{\partial y}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

$\textcolor{Red}{\textbf{Teorema de la Función Implicita (version sistemas de ecuaciones)}}$

Consideremos ahora el sistema

$au+bv-k_{1}x=0$
$cu+dv-k_{2}y=0$

con $a,b,c,d,k_{1},k_{2}$ constantes. Nos preguntamos cuando
podemos resolver el sistema para $u$ y $v$ en términos de $x$ y $y$.
Si escribimos el sistema como

$au+bv=k_{1}x$
$cu+dv=k_{2}y$

y sabemos que este sistema tiene solución si $det
\left|\begin{array}{cc} a&b\\
c&d\end{array}\right|\neq0$ en tal caso escribimos

$u=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b
\\c&d\end{array}\right|}(k_{1}dx-k_{2}by)$,~~$v=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b
\\c&d\end{array}\right|}(k_{2}ay-k_{1}cx)$.

Esta solución no cambiaría si consideramos

$au+bv=f_{1}(x,y)$
$cu+dy=f_{2}(x,y)$

donde $f_{1}$ y $f_{2}$ son funciones dadas de $x$ y $y$. La posibilidad de despejar las variables $u$ y $v$ en términos de $x$ y $y$ recae sobre los coeficientes de estas variables en las ecuaciones dadas.

Ahora si consideramos ecuaciones no lineales en $u$ y $v$ escribimos el sistema como

$g_{1}(u,v)=f_{1}(x,y)$
$g_{2}(u,v)=f_{2}(x,y)$

nos preguntamos cuando del sistema podemos despejar a $u$y $v$ en términos de $x$ y $y$. Mas generalmente, consideramos el problema siguiente, dadas las funciones $F$ y $G$ de las variables $u,v,x,y$ nos preguntamos cuando de las expresiones

$F(x,y,u,v)=0$
$G(x,y,u,v)=0$

podemos despejar a $u$ y $v$ en términos de $x$ y $y$ en caso de ser posible diremos que las funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ son funciones implícitas dadas. Se espera que $\exists’$n funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ en

$F(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$
$G(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$

con $(x,y)$ en alguna vecindad $V$. Suponiendo que existen $\varphi_{1}$ y $\varphi_{2}$ veamos sus derivadas

$\displaystyle \frac{\partial F}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial F}{\partial y}\displaystyle
\frac{\partial y}{\partial x}+\displaystyle \frac{\partial
F}{\partial u}\displaystyle \frac{\partial u}{\partial
x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle
\frac{\partial v}{\partial x}=0$ $~~ $ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial F}{\partial x}$

$\displaystyle \frac{\partial G}{\partial x}\displaystyle
\frac{\partial x}{\partial x}+\displaystyle \frac{\partial
G}{\partial y}\displaystyle \frac{\partial y}{\partial
x}+\displaystyle \frac{\partial G}{\partial u}\displaystyle
\frac{\partial u}{\partial x}+\displaystyle \frac{\partial
G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial x}=-\displaystyle \frac{\partial G}{\partial x}$

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas $\displaystyle \frac{\partial u}{\partial x}$ y $\displaystyle \frac{\partial v}{\partial x}$. Aquí se ve que para que el sistema tenga solución

$det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq0$ en $(P)$ (el $det$ Jacobiano) y según la regla de Cramer.

$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
x}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial x}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{\det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$, $~~$ $\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial x} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial x}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ $~~~~$ (con los dos $det$ Jacobianos).

Análogamente si derivamos con respecto a $y$ obtenemos

$\displaystyle \frac{\partial F}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial F}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=-\displaystyle \frac{\partial F}{\partial y}$

$\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=-\displaystyle \frac{\partial G}{\partial y}$

de donde
$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
y}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial y}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$, $~~$ $\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial y} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial y}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ $~~~~$ (con los dos $det$ Jacobianos).

Al determinante $det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle \frac{\partial
F}{\partial v}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|$ lo llamamos Jacobiano y lo denotamos por $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}$.

$\textcolor{Red}{\textbf{Teorema de la Función Implícita (sistemas de ecuaciones)}}$

$\textbf{Teorema 3.}$ Considere las funciones $z_{1}=F(x,y,u,v)$ y $z_{2}=G(x,y,u,v)$. Sea $P=(x,y,u,v) \in \mathbb{R}^{4}$ un punto tal que $F(P)=G(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{4}$ de centro $P$ las funciones $F$ y $G$ tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano $\displaystyle \frac{\partial
(F,G)}{\partial (u,v)}(P)\neq0$ entonces las expresiones $F(x,y,u,v)=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas) $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ definidas en una vecindad $v$ de $(x,y)$ las cuales tienen derivadas parciales continuas en $v$ que se pueden calcular como se menciona arriba.

$\small{Demostración}$ Dado que $$det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq 0$$ entonces $\displaystyle{\frac{\partial F}{\partial u}(p)}$, $\displaystyle{\frac{\partial F}{\partial v}(p)}$, $\displaystyle{\frac{\partial G}{\partial u}(p)}$, $\displaystyle{\frac{\partial G}{\partial v}(p)}$ no son cero al mismo tiempo, podemos suponer sin perdida de generalidad que $\displaystyle{\frac{\partial G}{\partial v}(p)}\neq0$. Entonces la función $z_{1}=G(x,y,u,v)$ satisface las hipótesis del T.F.I y en una bola abierta con centro p, v se puede escribir como $v=\psi(x,y,u)$.

Hacemos ahora
$$H(x,y,u)=F(x,y,u,\psi(x,y,u))$$ y tenemos que
$$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial F}{\partial u}\frac{\partial u}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}$$

por otro lado
$$\frac{\partial \psi}{\partial u}=-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}$$
por lo tanto
$$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\left(-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\right)=\frac{\frac{\partial F}{\partial u}\frac{\partial G}{\partial v}-\frac{\partial F}{\partial v}\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\neq0$$por lo tanto para $H(x,y,u)=0$ tenemos que existe una función $u=\varphi_{1}(x,y)$ y por lo tanto $v=\psi(x,y,u)=\psi(x,y,\varphi_{1}(x,y,u))=\varphi_{2}(x,y)$ y por tanto $u,v $ se pueden expresar en términos de $x,y$ en una vecindad de $p$. $\square$

$\textcolor{Red}{\textbf{El Teorema de la función implicita versión para funciones $f:\mathbb{R}\rightarrow\mathbb{R}$}}$

$\textbf{Teorema 1.}$ Considere la función $y=f(x)$. Sea $(x_{0},y_{0}) \in
\mathbb{R}^{2}$ un punto tal que $F(x_{0},y_{0})=0$. Suponga que la función $F$ tiene derivadas parciales continuas en alguna bola con centro $(x_{0},y_{0})$ y que $\displaystyle \frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$. Entonces $F(x,y)=0$ se puede resolver para $y$ en términos de $x$ y definir así una función $y=f(x)$ con dominio en una vecindad de $(x_{0},y_{0})$, tal que $y_{0}=f(x_{0})$, lo cual tiene derivadas continuas en $\mathcal{V}$ que pueden calcularse como $y’=f'(x)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$, $x \in \mathcal{V}$.

$\small{Demostración.}$ Como $\displaystyle{\frac{\partial
F}{\partial y}(x_{0},y_{0})\neq 0}$ supongamos sin perdida de generalidad que $\displaystyle{\frac{\partial F}{\partial y}(x_{0},y_{0})> 0}$. Por ser $\displaystyle{\frac{\partial F}{\partial y}}$ continua en una vecindad de $(x_{0},y_{0})$ entonces exite un cuadrado S, centrado en $(x_{0},y_{0})$ totalmente contenido en esa vecindad, en donde $\displaystyle{\frac{\partial F}{\partial y}(x,y)> 0}$ $\forall~x,y\in S$.Sea
$$S=\left\{(x,y)\in\mathbb{R}^{2}~|~|x-x_{0}|<h~y~|y-y_{0}|<k \right\}$$

En todo punto $(x,y)$ que pertenece a $S$, $\displaystyle{\frac{\partial F}{\partial y}(x,y)>0}$. Esto quiere decir que en $S$, $F$ es creciente y fijando $x_{0}$ en $[x_{0}-h,x_{0}+h]$ se tiene que $F$ es creciente en $[y_{0}-k,y_{0}+k]$ y se anula en $y_{0}$, por lo que
$$F(x_{0},y_{0}-k)<0~~yF(x_{0},y_{0}+k)>0$$ Consideremos ahora el par de funciones $F(x,y_{0}-k)$ y $F(x,y_{0}+k)$ definidas en el intervalo $(x_{0}-k,x_{0}+k)$. Donde ambas funciones solo tienen x como variable. La primera función cumple $F(x_{0},y_{0}-k)<0$ y por ser continua en $x_{0}$, es negativa en toda una vecindad $(x_{0}-h_{1}x_{0}+h_{1})$ de $x_{0}$. Análogamente, la segunda función cumple $F(x_{0},y_{0}+k)>0$ y por ser continua en $x_{0}$, es positiva en toda una vecindad $(x_{0}-h_{2}x_{0}+h_{2})$ de $x_{0}$. Sea $h=\min{h_{1},h_{2}}$. Entonces para toda $x$ tal que $|x-x_{0}|~y~F(x,y_{0}+k)>0$ Fijemos $x$ en el intervalo $(x_{0}-h,x_{0}+h)$, y consideremos a $F(x,y)$, sólo como función de $y$, sobre $[y_{0}-k,y_{0}+k]$. Esta función cumple que

$$F(x,y_{0}-k)<0~y~F(x,y_{0}+k)>0$$

por lo tanto según el teorema del valor intermedio, existe un único y en $(y_{0}-k,y_{0}+k)$ tal que $F(x,y)=0$. Así queda establecida la existencia y unicidad de la función $y=f(x)$. Donde además, $y_{0}=f(x_{0})$, y para todo $x\in(x_{0}-h,x_{0}+h)$ $$F(x,f(x))=0,y~~\frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$$

Vamos a comprobar que la función es continua, para ello se tiene
$$x\in[x_{0}-h,x_{0}+h]~\Rightarrow~|x-x_{0}|<h$$
tomando $h<\delta$ se tiene
$$|x-x_{0}|<\delta$$
esto quiere decir que
$$|y-y_{0}|<k$$ es decir$$|f(x)-f(x_{0})|,\frac{\partial F}{\partial y}(x_{0},y_{0})$$
existen y son continuas entonces $F$ es diferenciable por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k+R(h,k)$$
Tenemos que $F$ es continua por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=0sih,k\rightarrow 0$$
también
$$R(h,k)\rightarrow 0sih,k\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k=0$$
esto es
$$\frac{k}{h}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
y cuando $h,k\rightarrow 0$ se tiene
$$\frac{dy}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$

$\textbf{Importante:}$ Este es un resultado que garantiza la
existencia de una función $y=f(x)$ definida implícitamente por
$F(x,y)=0$. Esto es, puede resolverse para $y$ en términos de $x$,
pero no nos dice como hacer el despeje.

$\textbf{Ejemplo.}$ Considere la función $F(x,y)=e^{2y+x}+\sin(x^{2}+y)-1$ en el punto (0,0) tenemos $F(0,0)=0$. Las derivadas parciales de $F$ son
$F_{x}=e^{2y+x}+2x\cos(x^{2}+y)$
$F_{y}=2e^{2y+x}+\cos(x^{2}+y)$

que son siempre continuas. Además, $\displaystyle \frac{\partial F}{\partial y}(0,0)=3\neq0$ de modo que $\textbf{T.F.Im.}$ garantiza una vecindad de $x=0$ en la cual podemos definir una función $y=f(x)$ tal que $F(x,f(x))=0$. Obsérvese que en este caso no podemos hacer explícita la función $y=f(x)$ sin embargo tal función existe y su derivada es

$y’=f'(x)=\displaystyle -\frac{\displaystyle \frac{\partial F}{\partial x}}{\displaystyle \frac{\partial F}{\partial y}}=\displaystyle \frac{e^{2y+x}+2x\cos(x^{2}+y)}{2e^{2y+x}+\cos(x^{2}+y)}$

$\textbf{Ejemplo.}$ Considere $F(x,y)=x^{4}-e^{xy^{3}-1}$ en el punto (1,1) $F(1,1)=1-1=0$, $F_{x}=4x^{3}-y^{3}e^{xy^{3}-1}$ Por lo tanto, $F_{x}|{(1,1)}=3$, $F{y}=-3xye^{xy^{3}-1}$
Y así, $F_{y}|_{(1,1)}=-3$, y $\displaystyle \frac{\partial F}{\partial y}=-3\neq0$.

El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de (1,1) el nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es $y’=\displaystyle
\frac{-4x^{3}-y^{3}e^{xy^{3}-1}}{-3xy^{2}e^{xy^{3}-1}}$.

Observe que en este caso la función $F$ permite hacer el despeje en términos de $x$.

$F(x,y)=x^{4}-e^{xy^{3}-1}=0$
$x^{4}=e^{xy^{3}-1}$
$\ln (x^{4})=xy^{3}-1$
$\left(\displaystyle \frac{\ln (x^{4})+1}{x}\right)^{\frac{1}{3}}=y=f(x)$ que al derivar se debe de llegar al mismo resultado.

$\textbf{Ejemplo.}$ Considere $F(x,y)=x^{2}-y^{3}-1$ en el punto $(x_{0},y_{0})$ con $y_{0}\neq 0$ tal que $F(x_{0},y_{0})=0$, $F_{x}=2x,~~F_{y}=2y$
Por lo tanto, $F_{x}|{(x{0},y_{0})}=2x_{0}$,
Y así, $F_{y}|{(x{0},y_{0})}=2y_{0}$, y $\displaystyle \frac{\partial F}{\partial y}=2y_{0}\neq0$.
El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de $(x_{0},y_{0})$ el
nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es
$$y'(x)=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
en este caso
$$y'(x)=-\frac{2x_{0}}{2y_{0}}=-\frac{x_{0}}{y_{0}}$$
si $y_{0}>0$ tal función es $f(x)=\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{x}{\sqrt{1-x^{2}}}=-\frac{x}{y}$$
si $y_{0}<0$ tal función es $f(x)=-\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{-x}{-\sqrt{1-x^{2}}}=-\frac{x}{y}$$

$\textcolor{Red}{\textbf{El Teorema de la función implicita versión para funciones $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$}}$

Considere la función $F(x,y,z)$. Sea $(x_{0},y_{0},z_{0}) \in \mathbb{R}^{3}$ un punto tal que $F(x_{0},y_{0},z_{0})=0$. Suponga que la función $F$ tiene derivadas parciales $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y},~\frac{\partial F}{\partial z}}$ continuas en alguna bola con centro $(x_{0},y_{0},z_{0})$ y que $\displaystyle \frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\neq 0$.
Entonces $F(x,y,z)=0$ se puede resolver para $z$ en términos de $x,y$ y definir así una función $z=f(x,y)$ con dominio en una vecindad de
$(x_{0},y_{0},z_{0})$, tal que $z_{0}=f(x_{0},y_{0})$, lo cual tiene derivadas continuas
en $\mathcal{V}$ que pueden calcularse como $$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}~~~\frac{d z}{dy}(x,y)=-\displaystyle \frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$
$\textbf{Importante:}$ Este es un resultado que garantiza la existencia de una función $z=f(x,y)$ definida implícitamente por $F(x,y,z)=0$. Esto es, puede resolverse para $z$ en términos de $x,y$, pero no nos dice como hacer el despeje.

$\small{Demostración.}$ Consideremos el par de funciones
$$F(x,y,z_{0}-\ell)yF(x,y,z_{0}+\ell)$$
definidas para $(x,y)\in[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$\La primera satisface
$$F(x_{0},y_{0},z_{0}-\ell)<0$$ la segunda cumple $$F(x_{0},y_{0},z_{0}+\ell)>0$$
Fijemos $(x,y)$ en $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y consideramos $F(x,y,z)$ solo como función de z, sobre $[z_{0}-\ell,z_{0}+\ell]$. Esta función cumple
$$F(x,y,z_{0}-\ell)<0~y~F(x,y,z_{0}+\ell)>0$$
por lo que al aplicar el Teorema del valor intermedio, obteniendose un único z en $(z_{0}-\ell,z_{0}+\ell)$ en donde $F(x,y,z)=0$.Queda así establecida la existencia y unicidad de la función $z=f(x,y)$ con dominio $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y rango $[z_{0}-\ell,z_{0}+\ell]$ Vamos a probar que dicha f es continua, para ello si
$$\left(\begin{matrix}x\in [x_{0}-h,y_{0}+h] , y\in [y_{0}-k,y_{0}+k] \end{matrix}\right)~\Rightarrow~\left(\begin{matrix}|x-x_{0}|<h\|y-y_{0}|<k\end{matrix}\right)$$
por lo que
$$|(x,y)-(x_{0},y_{0})|<|x-x_{0}|+|y-y_{0}|<h+k$$
si $h<k$
$$|(x,y)-(x_{0},y_{0})|<2k=\delta$$
donde
$$|f(x,y)-f(x_{0},y_{0})|=|z-z_{0}|<\ell=\epsilon$$
por lo tanto $f(x,y)$ es continua.Ahora si suponemos que $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y}},~\frac{\partial F}{\partial z}$ son continuas en los alrededores de $(x_{0},y_{0},z_{0})$ en tonces F es diferenciable y se tiene
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$

De donde
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{h}{\ell}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
Análogamente
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$
De donde
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{k}{\ell}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dy}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$ $\square$